II. Economics Systems and Decision Making

Дата добавления: 2015-10-12; просмотров: 617

1. Цель работы:

Практическая проверка корректирующей способности избыточного кода на модели лабораторной установки, а также исследование характеристик системы передачи информации с решающей обратной связью (РОС).

2. Систематические коды:

Систематическими называют избыточный групповой n-значный код, каждая группа которого содержит m информационных и k=n-m контрольных символов, при этой расположение информационныхи контрольных символов в каждой группе неизменно [5].

Избыточное кодирование систематическим кодом (n,m) заключается в расчете контрольных символов для текущей m разрядной информационной группы и формирования n-разрядной группы избыточного кода. Правило вычисления контрольных символов называют правилом кодирования. На приемной стороне реализуется корректирующая способность избыточного кода: для принятой n-разрядной группы вычисляется исправляющий вектор, указывавший на номера ошибочно принятых разрядов. Исправление ошибочно принятых разрядов производится инвертированием символов этих разрядов. Правильное исправление ошибок проводится только в том случае, когда число ошибочно принятых разрядов (кратность ошибки) не превышает величины 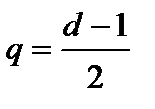, где d – кодовое расстояние избыточного n-значного кода. Правило вычисления исправляющего вектора называют правилом декодирования [6, 7].

При кодировании n-значным кодом возможно 2ⁿ различных кодовых груш (векторов). Из этого числа 2^m кодовых векторов являются разрешенными, которые и используются для передачи информации, поступающей на избыточное кодирование в виде m разрядных групп. Остальные векторы числом (2ⁿ - 2^m) не используются для передачи информации и называются запрещенными. Под правилом кодирования можно понимать правило, по которому устанавливается соответствие каждой m-разрядной информационной группе одного из 2^m разрешенных векторов n-значного избыточного кода. Под правилом декодирования можно понимать правило, по которому устанавливается соответствие каждому принятому n-значному вектору одного из разрешенных кодовых векторов.

Для построения избыточного кода, т.е. для определения раз­решенных n-значных кодовых векторов, а также правил кодиро­вания и декодирования, строятся производящая 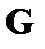и проверяющая матрицы. Производящая матрица 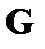имеет порядок 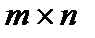, ее строками могут быть ненулевые n-значные векторы, содержащие не менее d-1 единиц, линейно независимые и отличающиеся друг от друга не менее чем в d-2 разрядах, где d – требуемое кодовое расстояние. Практически производящая матрица может быть построена дополнением единичной матрицы I порядка 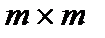к матрице 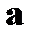порядка :

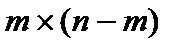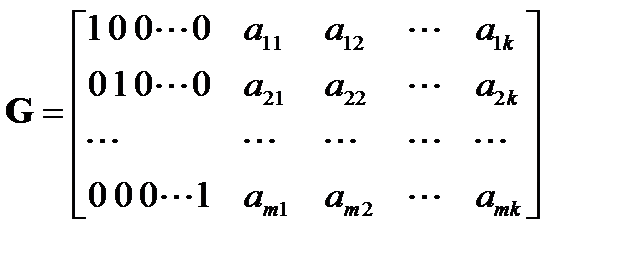(1)

Строки дополнительной матрицы 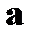должны содержать не менее d-1 единиц и различаться друг от друга не менее, чемв d-2 разрядах.

Производящая матрица определяет множество 2^m разрешенных векторов избыточного n-значного кода. Часть разрешённых векторов записана строками производящей матрицы (m векторов), остальная часть из 2^m -m-1 векторов находится в результате линейной комбинации строк производящей матрицы, т.е. суммированием по mod2 строк матриц в любых сочетаниях. Строки проверочной матрицы ортогональны строкам производящей матрицы 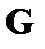. К разрешенным векторам относят также нулевой вектор.

Проверочная матрица имеет порядок 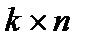и при задании производящей матрицы 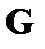в виде (1) может быть определена таким образом:

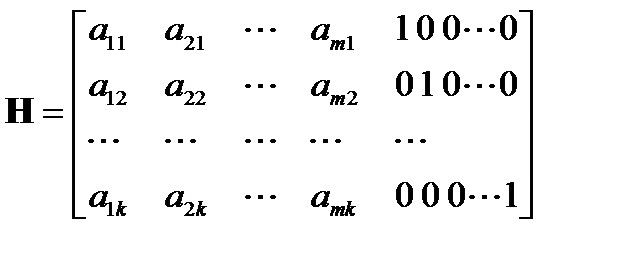(2)

Проверочная матрица линейной комбинацией строк порождает множество векторов 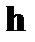, ортогональных всем разрешенным векторам кода. Как известно, условие ортогональности двух векторов 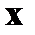и 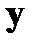выражается соотношением

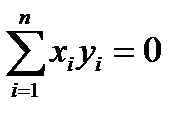, (3)

где сумма рассматривается по mod2.

Проверочная матрица необходима для вычисления исправляющего вектора 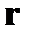, который находится в результате матричного произведения

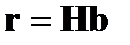(4)

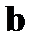проверочной матрицы на принятый вектор . Алгоритм (4) определяет правило декодирования в виде k проверок (по числу строк проверочной матрицы) на чётность:

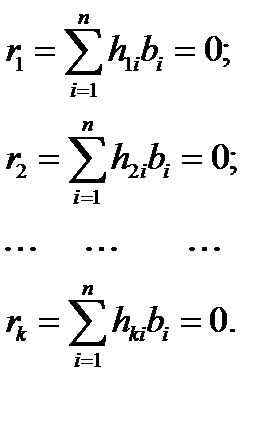(5)

В результате этих проверок вычисляются разряды исправляющего вектора 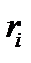. Если все проверки дают нулевую сумму (сумма по mod2), то ошибка не фиксируется. При этом либо её нет совсем, либо её кратность выходит за пределы корректирующей способности кода. И в том и в другом случае нулевые суммы 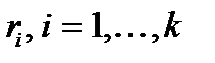являются свидетельством ортогональности принятого вектора 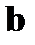векторам 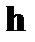, что указывает на принадлежность принятого вектора множеству разрешимых векторов. При ненулевом векторе 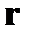фиксируется факт ошибочного приема отдельных разрядов переданного вектора. Если кратность ошибки не превышает допустимой величины, при которой возможно иcправление ошибок, то по вычисленному вектору 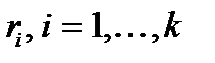можно однозначно определить номера ошибочно принятых разрядов, пользуясь заранее подготовленной таблицей соответствия. Такая таблица устанавливает соответствие каждому вектору 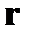определённого номера и или комбинации номеров ошибочно принятых разрядов.

В лабораторной работе изучается систематический код (7,4). Такой код имеет расстояние 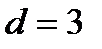и, следовательно, на приёмной стороне возможно исправление однократных ошибок. Другими словами, код обладает корректирующей способностью при условии искажения только одного разряда 7-разрядной группы.

Код (7,4) может быть построен с различными правилами кодирования и декодирования. Построим код по изложенной выше методике. Производящую матрицу 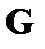запишем в виде

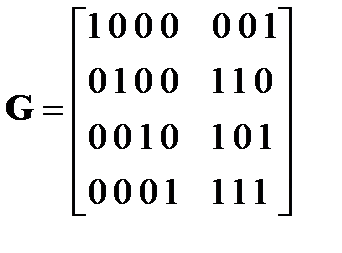(6)

Тогда проверочная матрица примет вид:

(7)

Непосредственными вычислениями нетрудно убедиться в ортогональности любой пары векторов из множеств 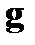и 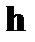, порождаемых матрицам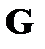и и соответственно.

Правила декодирования согласно соотношениям (4) выра­жается тремя проверками на четность:

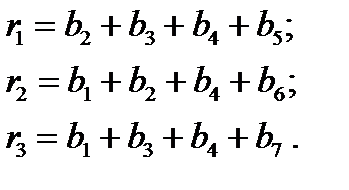(8)

В каждой проверке участвует определенная подгруппа разрядов принятого 7-значного вектора 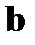. В результате проверок вычисляется исправляющий вектор 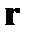. Построим таблицу соответствия каждому вектору 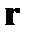номера ошибочно принятого разряда. Если ошибка произошла в разряде 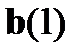и только в этом разряде, то 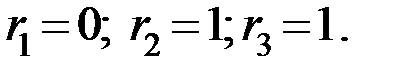При ошибочном приеме разряда 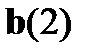значения исправляющего вектора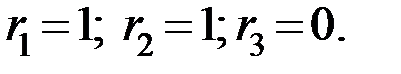

Продолжая вычисления, приходим к выводу, что искомая таблицасоответствия дается проверочной матрицей, если столбцы этой матрицы рассматривать в качестве векторов 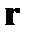. При этом номер столбца, к которому относится вычисленный вектор 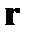и есть номер ошибочно принятого разряда.

Проверочная матрица задает и правила кодирования, т.е. правила вычисления контрольных разрядов. За контрольные разряды удобно принять такие, которые входят в каждую проверяемую подгруппу один раз. Для рассматриваемого кода (7,4) за контрольные разряды 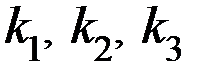следует принять последние три разряда 7-значного вектора 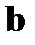: 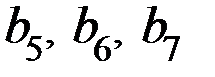, а информационную группу разрядов 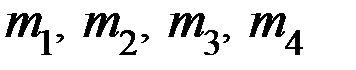разместить на позициях первых четырёх разрядов: 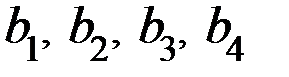. Контрольный разряд должен дополнять свою подгруппу дочетного числа единиц. Поэтому правила кодирования, записанные на основании (8) ипринятого размещении контрольных и информационных разрядов, принимают вид:

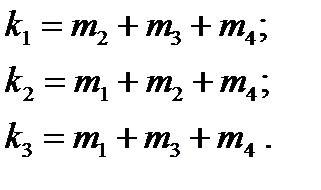(8)

Код (7,4) можно построить и так, чтобы исправляющий вектор в двоичном исчислении непосредственно давал номер ошибочного принятого разряда. Очевидно, в этом случае проверочная матрица должна иметь вид:

(9)

Код с проверочной матрицей данного вида называют кодом Хемминга [7].

Правило образования разрядов исправляющего вектора получается при записи всех разрядов 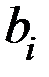в виде двоичного кода, т.е.

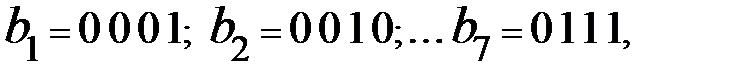
и каждая проверка есть сумма по mod2 всех разрядов, в номерах которых 1 стоит в младшем ( 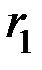), во втором ( 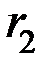) и третьем ( 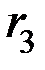) разрядах кода, т.е.

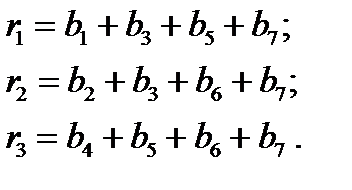(10)

Уравнения кодирования (с учетом расположения контрольных разрядов на последних позициях 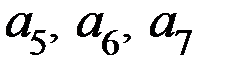7-значного кода) будут получены путем приравнивания проверочных уравнений 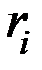нулю в виде

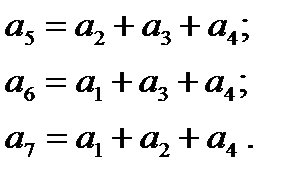(11)

Характеристики кода Хемминга приведены втаблице [7].

Таблица 1 Характеристики кода Хемминга

Число возможных ошибок	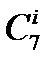Кратность ошибки
Число необнаруженных ошибок

3. Описание лабораторной установки:

Избыточное помехоустойчивое кодирование цифровой информации в зависимости от организации работы системы передачи и её условий работы может быть использовано по-разному.

Так, в радиолиниях связи чаще всего корректирующие коды используются для исправления ошибок малой кратности (1,2) при передаче дискретной информации – команд, разовых измерений, букв. При передаче непрерывной информации кодовым методом между отсчетами сообщения, как правило, существует значительная статистическая или функциональная связь. В этом случае предпочтительнее использовать корректирующую способность кода для обнаружения ошибок и стирания неправильных кодовых комбинаций (отсчётов сообщения). Возможно также совместное использование в радиолиниях исправляющей и обнаруживающей способности кода. В тех случаях, когда скорость передачи информации менее важна, чемеё помехоустойчивость, применяются системы связи с обратным каналом. При этом корректирующая способность кода в большей степени используется для обнаружения ошибок. При обнаружении ошибки на приемной стороне на передающую сторону посылается сигнал на повторение неправильно принятой комбинации. Повторение производится до тех пор, пока не будет принята информация без ошибок. При этом получателювыдаются либо безошибочные кодовые комбинации, либо комбинации, в которых произошла необнаруженная ошибка. Ошибочныекомбинации могут быть получены, если необнаруженная ошибка возникла при 1-й передаче, либо при повторениях с обнаружением, а при N+1 повторении возникает необнаруженная ошибка. Вероятность остаточной ошибки при этом может быть получена как и характеризует качество системы с переспросом.

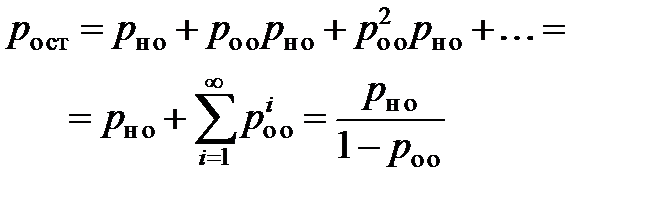(12)

Для конкретной помеховой ситуации величины 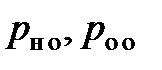зависят от свойств кода.

Основным назначением исследуемой лабораторной установки является изучение одного из методов избыточного кодирования корректирующим систематическим кодом (7,4) в системе с обратным каналом и неограниченным числом переспросов, измерение и расчет некоторых характеристик системы ( ).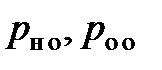

Установка состоит из следующих основных частей:

1. 4-разрядный датчик информационного двоичного кода.

2. Кодирующее устройство, реализующее код (7,4).

3. Прямой канал связи для последовательного способа передачи кода.

4. Датчик искажений в линии связи.

5. Приемный регистр 7-разрядного кода.

6. Схема коррекции, обнаруживающая и исправляющая ошибки.

7. Входной регистр приемника для 4информационных разрядов.

8. Обратный канал связи.

9. Схема регистрации ошибок в канале связи.

10.Схема индикации результатов эксперимента.

11.Схема управления и синхронизации работы установки.

Функциональная схема лабораторной работы № 6 приведена на рисунке 1.

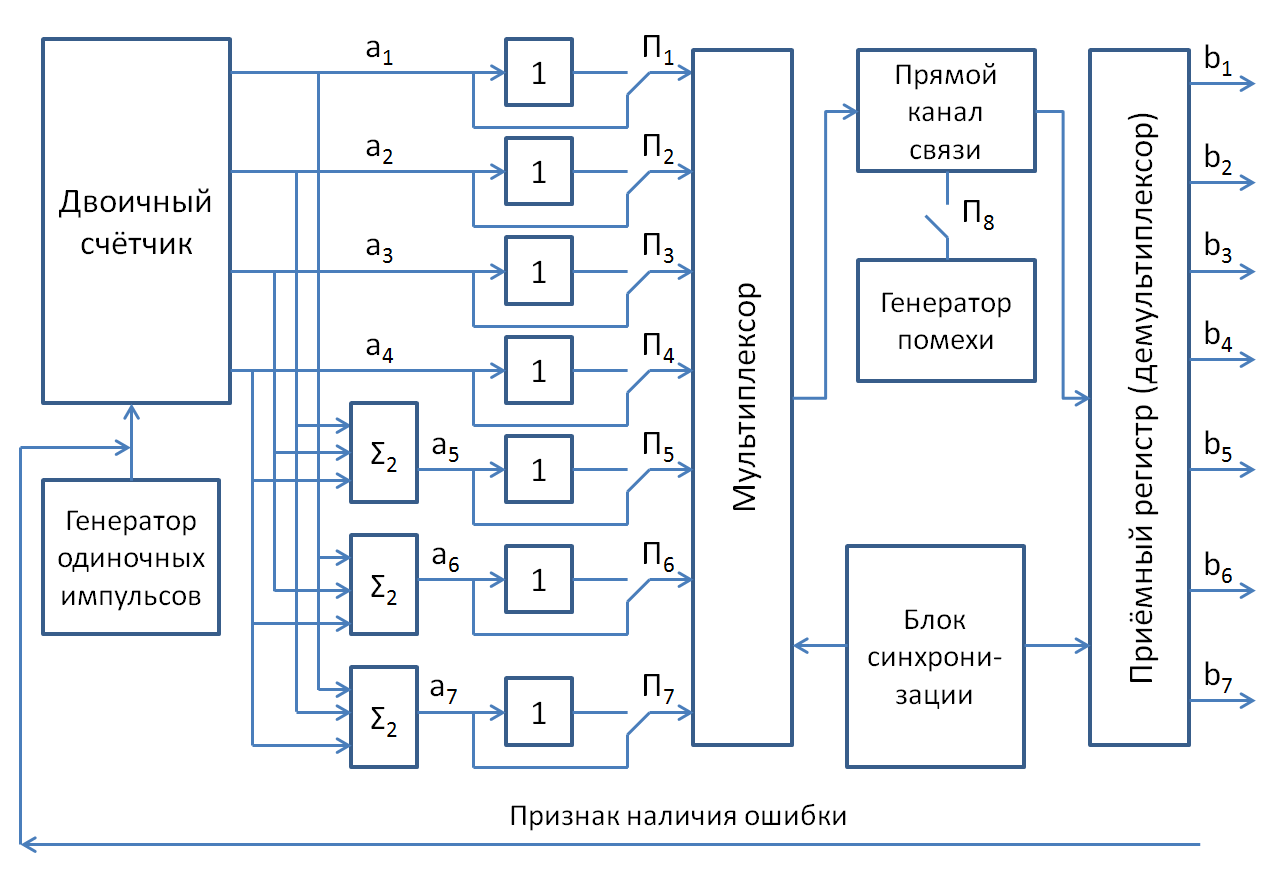
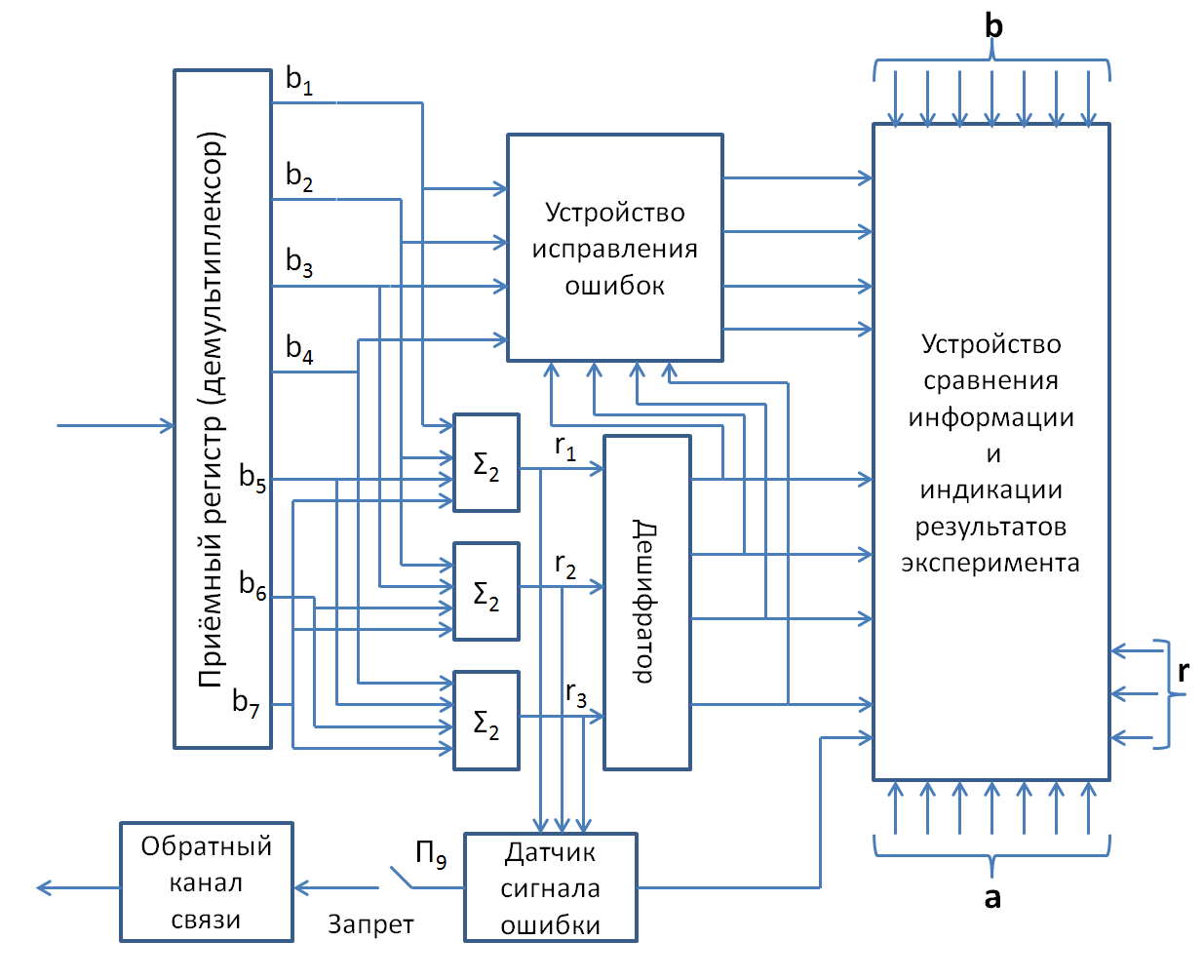
Рисунок 1 – Упрощенная функциональная схема лабораторной установки

Датчик информации представляет собой двоичный счетчик, который при подаче на него запускающих импульсов позволяет реализовать любую кодовую комбинацию 4~разрядного двоичного кода. Смена информации в датчике может производиться как вручную – последовательным нажатием кнопки, так и автоматически. По сигналу обнаружения ошибки, поступающему с обратного канала, смена кодовой комбинации в датчике информации запрещается.

Кодирующее устройство формирует значения трёх проверочных разрядов кода. Оно выполнено на сумматорах по модулю 2. Кодирование и запись в передающий регистр происходит в параллельном потенциальном коде.

В линии связи происходит последовательная передача кода. Для этого тактовый генератор производят последовательное считывание информации с разрядов передающего регистра, формируя кодовые посылки, следующие с частотой F = 1000 Гц. Длительность кодовой группы приблизительно в 8 раз меньше периода ее повторения. Пауза между группами кодов используется для работы схем обнаружения и исправления ошибок на приёмной стороне. Приёмный регистр линии связи преобразует последова­тельный код в параллельный, и работа последующих устройств происходит по окончании записи кода.

Датчик искажений инвертирует значение разряда кода на противоположный при совпадении импульса генератора хаотической импульсной помехи (ХИП) с соответствующим разрядом кода. Меняя интенсивность появления импульсов ХИП, можно обеспечить различное значение вероятности ошибки и её кратность. Искажения передаваемых кодов в установке можно также вводить вручную тумблерами П1–П7 "Искажения разрядов".

Схема коррекции ошибок состоит из логических схем, формирующих исправляющий вектор – сумматоров по модулю 2, дешифратора, который определяет ошибочно принятый разряд и формирует истинное значение искаженного информационного разряда. Эта же схема используется для формирования признака "обнаружения" и "необнаружения" ошибок в 7-разрядной группе, но yжe без определения номера искажённого разряда. При необнаружении ошибки по обратному каналу передается импульсный сигнал разрешения, с приходом которого код на выходе датчика информации изменяется. При обнаружении ошибки кодовая комбинация на датчика не изменяется и передается до тех пор, пока она не будет принята правильно или возникнет необнаруживаемая ошибка.

Выходной регистр приемника формирует значения информационных разрядов для получателя после схемы коррекции ошибок и выдает на индикацию значение выходного кода и номер разряда, в котором произошла одиночная ошибка.

Схема регистрации ошибок (блок сравнения) работает на принципе антисовпадения, регистрируя несовпадения передающего и принятого информационного кода без логической обработки. Таким образам, эта схема фиксирует все комбинации, поступившие на приемную сторону с ошибками.

Схема управления обеспечивает следующие режимы работы установки:

а) "ручной режим" с разовым набором информационных кодов, введением искажений в разряды и разовой передачей кода (7,4). Этот режим служит для изучения корректирующих возможностей кода и логики работы схем кодирования и декодирования. Работа в этом режиме осуществляется кнопками "Ручной набор кода" и "Передача". Состояния соответствующих регистров передатчика и приемника показываются в схеме индикации;

б) "автоматический режим" с периодической сменой информационных кодов, которая производится с частотой F = 1500 Гц. В автоматическом режиме кодовые группы передаются через линию связи с помехами, где подвергаются искажениям. На приемной стороне ошибки обнаруживаются. При включенном обратном канале ошибочно принятые комбинации повторяются.

Характеристики системы для различных режимов можно снять, фиксируя общее число обнаруженных ошибок N₀₀ и число ошибочных кодов N_общ при различном уровне помех в канале связи. Уровень помех регулируется ручкой "Интенсивность ХИП".

Регистрация числа ошибок производится двумя счетчиками импульсов, включенными параллельно, т.е. все управление ведется с одного счетчика командами "Сброс" - "Пуск". Необходимое время измерения (Т_изм = 30 с) устанавливается переключателем "Экспозиция" на обоих счетчиках.

Структурная схема Simulink-модели, соответствующая реальной установке, изображённой на рисунке 1, приведена на рисунке 2. На верхней половине рисунка 2 представлена модель передающей части вместе с каналом связи и источником помех, на нижней половине – модель приёмной части вместе с регистраторами и сравнивающими устройствами.

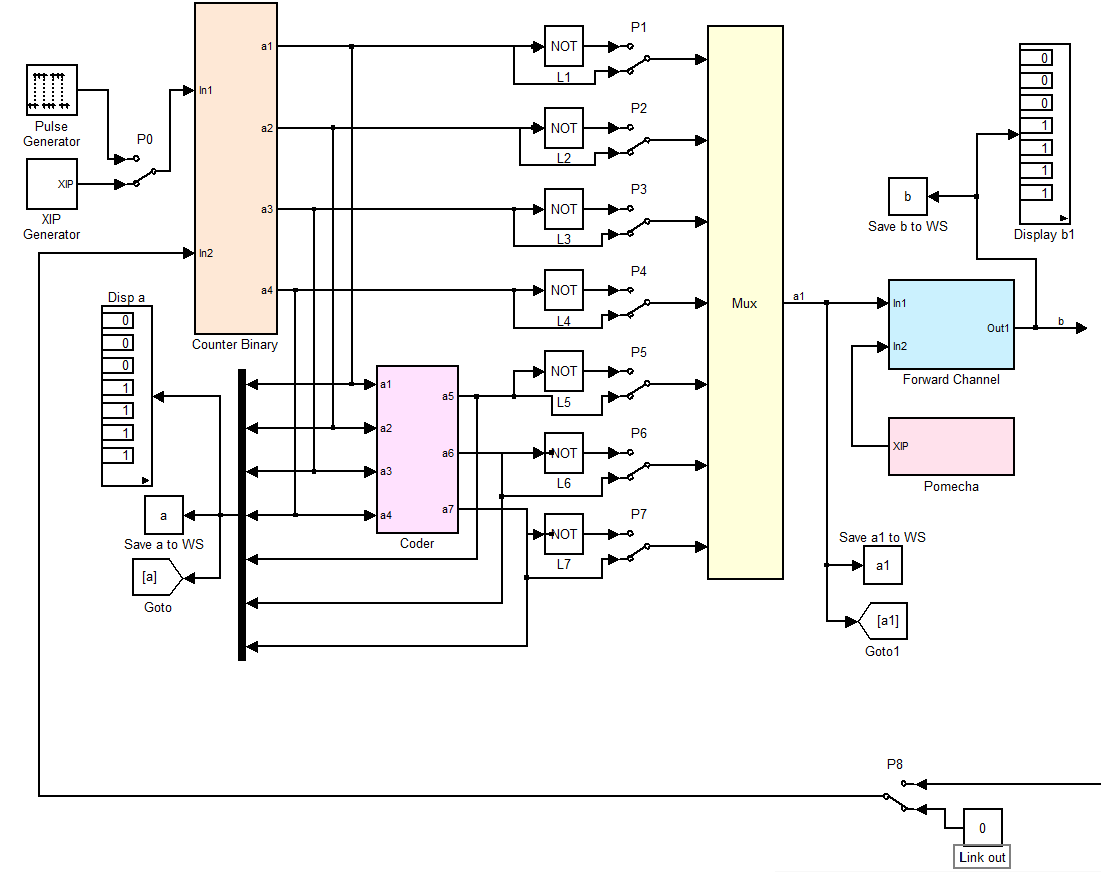
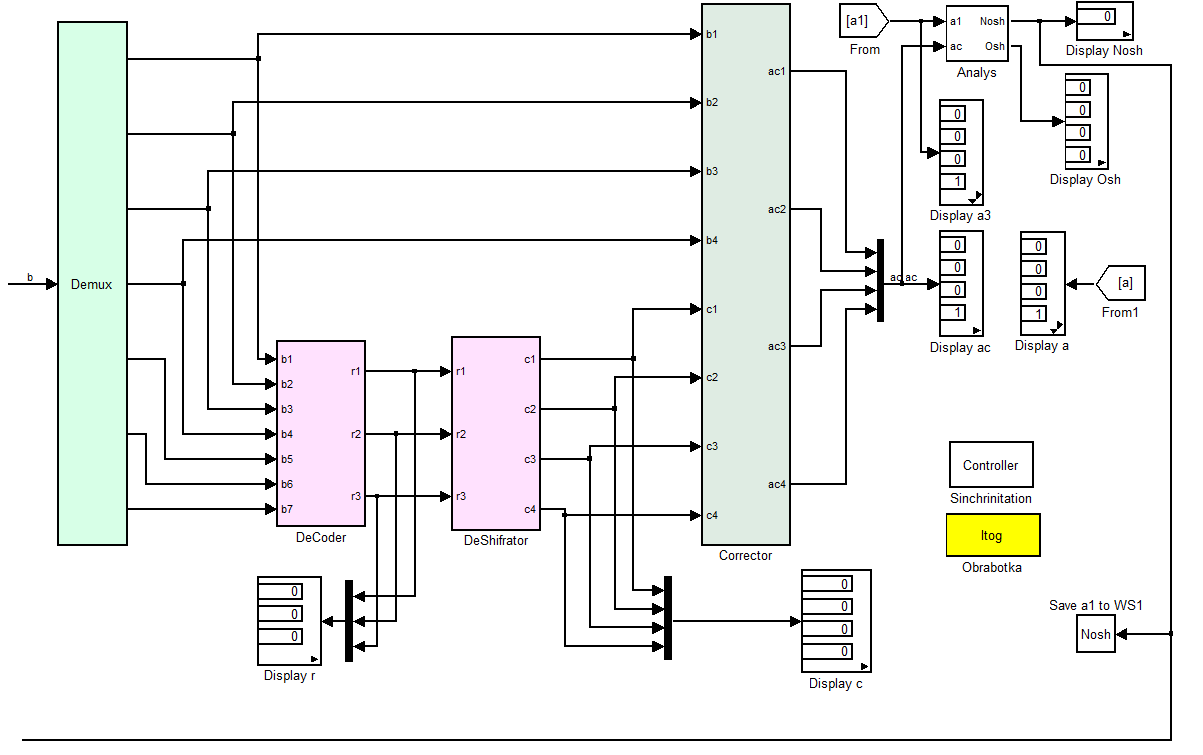
Рисунок 2 – Блок-схема модели для исследования статистических

характеристик систематического кода (7,4)

В передающей части информационный код формируется двоичным 4-х разрядным счётчиком либо от генератора периодически следующих импульсов Pulse Generator, либо от генератора хаотически следующих импульсов XIP Generator. Частота следования импульсов равна 1 Гц. На этой фиксированной частоте работает вся Simulink-модель установки. Весь процесс формирования кода, его прохождения через канал связи и обработки выполняется за один такт, т.е. за 1 секунду. Сформированный счётчиком и дополненный проверочными битами 7-разрядный код назван 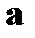, после ручного ввода (переключатели P1-P7) ошибок – 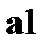, а его изменённый образ после прохождения через канал связи с помехами – 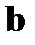. Уровень помех задаётся в блоке Pomecha установкой числового значения вероятности битовой ошибки (BER) в пределах от 0 до 1.

На приёмной стороне из принятого кода 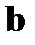в блоке декодирования DeCoder формируется код ошибки 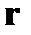, на основе которого в блоке дешифрации Deshifrator определяются номера ошибочно принятых разрядов кода 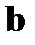. Информация об ошибочно принятых разрядах в виде 4-х разрядного кода 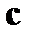передаётся в блок коррекции Corrector, где у принятого кода 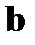инвертируются ошибочно переданные разряды. Код, полученный в результате коррекции, называется 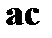. В блоке Analysis он сравнивается с переданным кодом 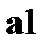, подсчитывается число ошибочно принятых разрядов Nosh и формируется сигнал ошибки в виде числа, равного 1, если ошибки есть, и 0, если их нет.

Для сравнения откорректированного принятого кода 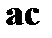из рабочего пространства (WS = Work Space) системы MATLAB вызывается первоначальный (истинный, не подвергавшийся ручной модификации) код .

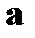Включение и отключение обратной связи выполняется переключателем P8.

Установка позволяет исследовать свойства систематического кода (7,4) как в пошаговом режиме, так и на определённом интервале дискретного времени. Управление режимами проводится с помощью блока Synchronization указанием числа тактов (временных шагов).

Статистические характеристики свойств кода (7,4) можно посмотреть в дополнительном окне (рисунок 3), которое вызывается при щёлке мышью по блоку Obrabotka.

Рисунок 3 – Окно вывода результатов исследования статистических
характеристик систематического кода (7,4)

4. Подготовка к лабораторной работе:

В процессе домашней подготовки необходимо выполнить:

4.1. Ознакомиться с теоретическими сведениями и лабораторной установкой по методическому описанию и учебной литературе из предложенного списка. Сопоставить описание натурной лабораторной установки с её Simulink-моделью, выявить различия в их структурных схемах.

4.2. Исходя из правила декодирования, используемого в установке, найти примеры обнаруживаемых и необнаруживаемых ошибок высокой кратности.

4.3. Определить следующие характеристики используемого кода (7, 4):

– коэффициент обнаружения ;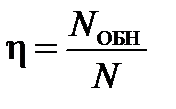

– вероятность необнаруженной ошибки 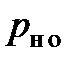для ;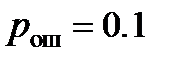

– вероятность остаточной ошибки 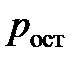для системы с обратной связью и бесконечным числом переспросов для .

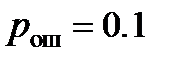4.4. Продумать методику измерений и вычислений следующих характеристик установки:

– скорость передачи информации при отсутствия искажений;

– скорость получения информации с обратным каналом при наличии помех;

– вероятности ошибки в одном разряде .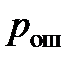

4.5. Подготовить ответы на контрольные вопросы.

5. Лабораторное задание:

5.1. Убедиться на примерах в корректирующей способности кода при наличии только однократных ошибок.

5.2.Убедиться в способности кода обнаруживать одно- и двукратные ошибки, а в отдельных случаях ошибки и более высокой кратности.

5.3.Проверить факт необнаружения ошибки высокой кратности, определённых в п. 3 домашнего задания.

5.4.Определить скорость передачи кодовых групп R 1/с.

5.5.Изменяя интенсивность хаотической импульсной помехи (ХИП) от минимума (0) до максимума (1), измерить в автоматическом режиме за T_изм = 2^14 с общее число ошибочных кодовых групп 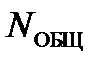и число кодовых групп с обнаруженными ошибками.

5.6.По данным измерений вычислить и построить зависимости вероятностей 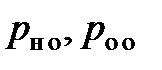от эквивалентной вероятности искажения разряда кода 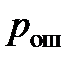(вероятности битовой ошибки BER). Сравнить в одной из точек результат эксперимента и расчета.

Методические указания для проведения расчётов. По результатам эксперимента при проведении работы определяются:

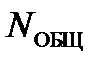– общее число ошибок в канале связи за время T_изм =
= 2^14 с;

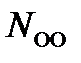– число обнаруженных ошибок за время T_изм =
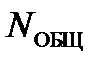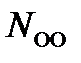= 2^14 с при различных интенсивностях помех в канале связи. Величины и характеризуют число ошибок для всей 7- разрядной кодовой комбинации.

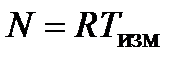– общее число переданных кодов, где

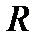(код/с) –скорость передачи кодовых групп.

Пользуясь результатам эксперимента, можно рассчитать вероятности:

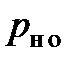– необнаружения ошибки в виде ;

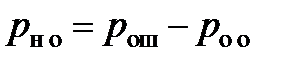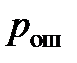– эквивалентная вероятность искажения одного разряда кода, определяемая из соотношения

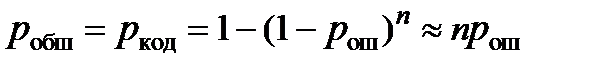, если 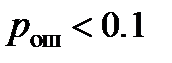и при этом предполагается, что ошибки возникают в разрядах независимо;

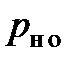– необнаружения ошибки в виде ;

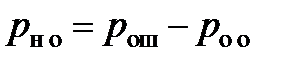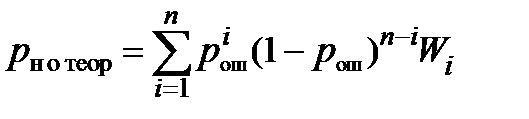– теоретическая вероятность необнаружения ошибки.

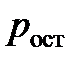– остаточная вероятность необнаружения ошибки применяемого кода (7,4) в системе с ОС, где

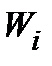– число необнаруживаемых кратных ошибок в коде (дано в таблице).

6. Требования к отчету:

Отчет должен содержать:

1) формулировку целей и задач лабораторной работы;

2) функциональную схему и блок-схему Simulink-модели экспериментальной установки;

3) результаты домашней подготовки;

4) результаты лабораторных экспериментов;

5) выводы по результатам теоретических и экспериментальных исследований с обсуждением причин их несовпадений.

7. Контрольные вопросы:

7.1. Какой избыточный код реализован вустановке?

7.2. Сколько различных модификаций имеет систематический
код (7,4)? Чей они могут различаться?

7.3. Отобразить логику работы дешифрватора.

7.4. Как определяются правила кодирования и декодирования по заданной проверочной матрице?

7.5. Как по результатам эксперимента оценить вероятность искажения одного разряда кодовой группы?

7.6. За единицу времени передается R кодовых групп. Из этого числа A групп поступает на приёмную сторону с ошибками. Наличие ошибок установлено в В группах. Оценить по этим данным вероятность ошибочной выдачи кодовой группы в СПИ с решающей обратной связью.

7.7. Как определить экспериментально скорость передачи кодовых групп, реализованную в лабораторной установке?

7.8. Известна вероятность искажения 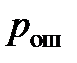одного разряда кодовой группы. Определите вероятность передачи без ошибок кодовой группы.

7.9. Корректирующую способность кода (7,4) можно использовать для исправления ошибок или для обнаружения ошибок. Что выгоднее?

7.10. Будет липередаваться информация при одновременном включении искажения разряда и ХИП в системе с ОС?

7.11. Составить циклограмму работы установки с ОС (по приведённому выше описанию).

Лабораторная работа № 7