Хлоридна кислота

Дата добавления: 2015-10-12; просмотров: 852

Если 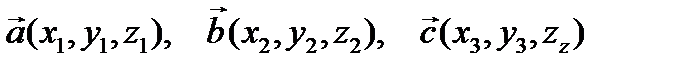, то .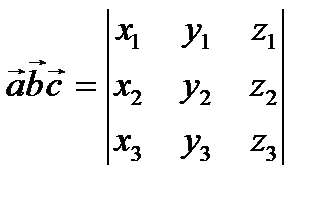

Приложения смешанного произведения:

1) 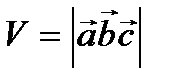- объем параллелепипеда;

- объем пирамиды, построенной на векторах ;

2) векторы компланарны тогда и только тогда, когда .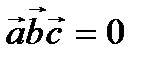

Пример 14.3. По координатам вершин пирамиды 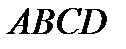найти:

1) объем пирамиды ;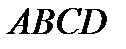

2) длину высоты пирамиды 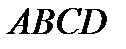, опущенную из вершины ;

; ; ; .

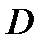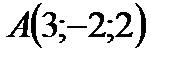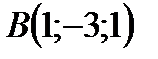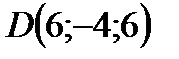Решение: Найдем объем пирамиды :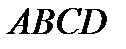

.

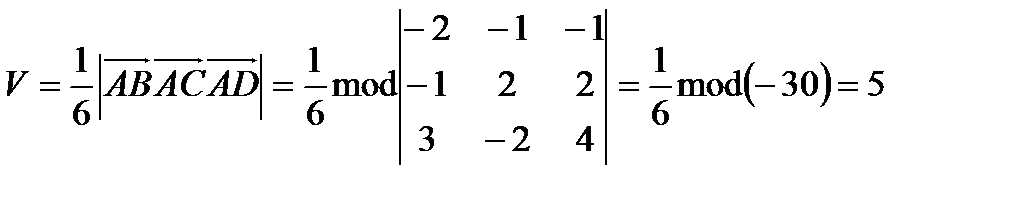Ответ: .

4) Найдем длину высоты пирамиды 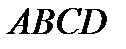, опущенную из вершины :

.

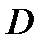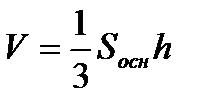
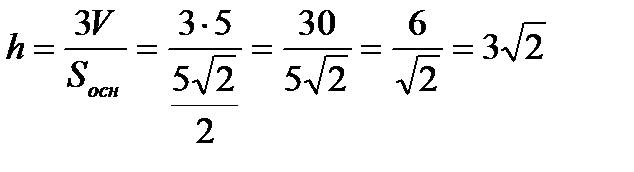Ответ: .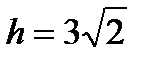

Решить задачи:

39. Найти смешанное произведение векторов, если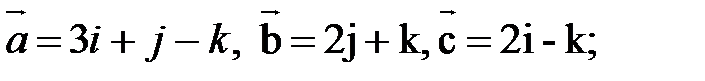

40. Найти смешанное произведение векторов, если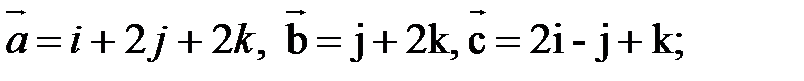

41. Определить, какой является тройка (правой или левой), если 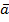= i + j, 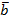= i – j, c = k.

42. Установить колпларны ли векторы если : = {2; 3; -1}, 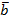= {1; -1; 3} и = {1; 9; -11}.

43. Даны вершины тетраэдра А(2; 3; 1), В (4; 1; -2), С (6; 3; 7) и D (-5; -4; 8). Найти длину его высоты, опущенной из вершины D.

44. Доказать, что векторы , удовлетворяющие условию 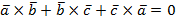компланарны.

45. Доказать, что | | | 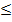| | 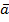| | |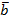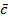; в каком случае здесь может иметь место знак равенства?

46. Доказать, что четыре точки А (1; 2; -1), В (0; 1; 5), С (-1; 2; 1) и D (2; 1; 3) лежат в одной плоскости.

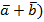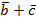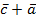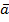47. Доказать тождество ( ( ) ( ) = 2 6 .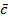

Задание домой: готовиться к контрольной работе.

48. Вектор перпендикулярен к векторам 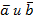равен 30 . Зная, что | 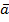| = 6, | 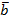| = 3, | 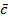| = 3, вычислим .

49. Установить, компланарны ли векторы , если : 2) : = {3; -2; 1}, 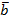= {2; 1; 2}, = {3; -1; -2}. 3) = {2; -1; 2}, 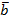= {1; 2; -3} и = {3; -4; 7}.

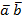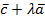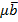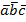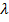50. Доказать тождество ( + ) = , где и 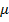- какие угодно числа.

51. Объем тетраэдра V = 5, три его вершины находящиеся в точках А (2; 1; -1), В (3; 0; 1) и С (2; -1; 3). Найти координаты четвертой вершины D, если известно, что она лежит на оси ОУ.

Практическое занятие 16

Комплексные числа.