Про організацію додаткових освітніх послуг

Дата добавления: 2015-10-15; просмотров: 514

Составить программу вычисления суммы ряда с заданной точностью e. Анализируя код программы, выявить возможные причины возникновения исключений и ввести их обработку, обеспечивающую вывод типа исключения и пояснение к причине его возникновения.

1.Вычислить с точностью e

- приближенное значения функции ln(1+X)/X по формуле
,
используя смешанный способ вычисления члена ряда,

- точное значение функции ln(1+X)/X,

- абсолютную и относительную ошибки приближенного значения.

2.Вычислить с точностью e

- приближенное значения функции 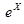по формуле
,
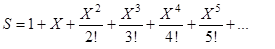используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,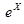

- абсолютную и относительную ошибки приближенного значения.

3.Вычислить с точностью e

- приближенное значения функции sinX по формуле
,
используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции sinX,

- абсолютную и относительную ошибки приближенного значения.

4.Вычислить с точностью e

- приближенное значения функции по формуле
,
используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,

- абсолютную и относительную ошибки приближенного значения.

5.Вычислить с точностью e

- приближенное значения функции arcsinX по формуле
,
используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции arcsinX,

- абсолютную и относительную ошибки приближенного значения.

6.Вычислить с точностью e

- приближенное значения функции arctgX по формуле
,
используя смешанный способ вычисления члена ряда,

- точное значение функции arctgX,

- абсолютную и относительную ошибки приближенного значения.

7.Вычислить с точностью e

- приближенное значения функции по формуле
,
используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,

- абсолютную и относительную ошибки приближенного значения.

8.Вычислить с точностью e

- приближенное значения функции по формуле
,
используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,

- абсолютную и относительную ошибки приближенного значения.

9.Вычислить с точностью e

- приближенное значения функции ln(1-X) по формуле
,
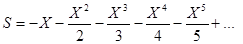используя смешанный способ вычисления члена ряда,

- точное значение функции ln(1-X),

- абсолютную и относительную ошибки приближенного значения.

10.Вычислить с точностью e

- приближенное значения функции 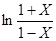по формуле
,
используя смешанный способ вычисления члена ряда,

- точное значение функции ,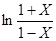

- абсолютную и относительную ошибки приближенного значения.

11.Вычислить с точностью e

- приближенное значения функции 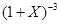по формуле
,
используя смешанный способ вычисления члена ряда,

- точное значение функции ,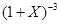

- абсолютную и относительную ошибки приближенного значения.

12.Вычислить с точностью e

- приближенное значения функции по формуле
,
используя смешанный способ вычисления члена ряда,

- точное значение функции ,

- абсолютную и относительную ошибки приближенного значения.

13.Вычислить с точностью e

- приближенное значения функции по формуле
,
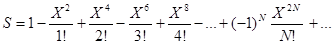используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,

- абсолютную и относительную ошибки приближенного значения.

14.Вычислить с точностью e

- приближенное значения функции по формуле
,
используя смешанный способ вычисления члена ряда,

- точное значение функции ,

- абсолютную и относительную ошибки приближенного значения.

15.Вычислить с точностью e

- приближенное значения функции по формуле
,
используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,

- абсолютную и относительную ошибки приближенного значения.

16.Вычислить с точностью e

- приближенное значения π по формуле
,
используя смешанный способ вычисления члена ряда,

- точное значение π с помощью стандартной функции Pi,

- абсолютную и относительную ошибки приближенного значения.

17.Вычислить с точностью e

- приближенное значения по формуле
,
используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции,

- абсолютную и относительную ошибки приближенного значения.

18.Вычислить с точностью e сумму бесконечного ряда

,

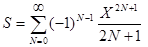- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

19.Вычислить с точностью e сумму бесконечного ряда

,

- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

20.Вычислить с точностью e сумму бесконечного ряда

,

- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

21.Вычислить с точностью e сумму бесконечного ряда

,

- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

22.Вычислить с точностью e сумму бесконечного ряда

,

- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

23.Вычислить с точностью e сумму бесконечного ряда

,

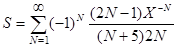- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

24.Вычислить с точностью e сумму бесконечного ряда

,

- используя смешанный способ вычисления члена ряда,

- используя рекуррентную формулу для вычисления члена ряда.

25.Вычислить с точностью e сумму бесконечного ряда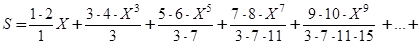

,

- используя смешанный способ вычисления члена ряда,

- используя рекуррентную формулу для вычисления члена ряда.

26.Вычислить с точностью e сумму бесконечного ряда ,

используя смешанный способ вычисления члена ряда.

27. Вычислить с точностью e сумму бесконечного ряда
,

- используя рекуррентную формулу для вычисления члена ряда,

- используя смешанный способ вычисления члена ряда.

Вычисление суммы бесконечного ряда с заданной точностью

Пусть задана последовательность чисел R₁, R₂, R₃,…,R_n,…. Выражение
R₁ + R₂ + R₃ +…+ R_n +… называют бесконечным рядом, или просто рядом, а числа R₁, R₂, R₃,… - членами ряда. При этом имеют в виду, что накопление суммы ряда начинается с первых его членов. Сумма S_n = называется частичной суммой ряда: при n=1 – первой частичной суммой, при n=2 – второй частичной суммой и так далее.

Называется ряд сходящимся, если последовательность его частичныхсумм имеет предел, и расходящимся – в противном случае. Понятие суммы ряда можно расширить [9], и тогда некоторые расходящиеся ряды также будут обладать суммами. Именно расширенное понимание суммы рядабудет использовано при разработке алгоритмов при следующей постановке задачи: накопление суммы следует выполнять до тех пор, пока очередной член ряда по абсолютной величине больше заданной величины ε.

В общем случае все или часть членов ряда могут быть заданы выражениями, зависящими от номера члена ряда и переменных. Например,

Тогда возникает вопрос, как минимизировать объём вычислений - вычислять значение очередного члена ряда по общей формуле члена ряда(в приведённом примере её представляет выражение под знаком суммы), по рекуррентной формуле (её вывод представлен ниже) или использовать рекуррентные формулы лишь для частей выражения члена ряда (см. ниже).