Тема 9. Фінансові послуги з прийняття ризику

Дата добавления: 2015-10-15; просмотров: 559

Типичным представителем класса задач, для которых подходит представление (формализация) в пространстве состояний, является головоломка, известная как игра в пятнадцать. В ней используется пятнадцать пронумерованных (начиная с 1) подвижных фишек, расположенных в клетках квадрата 4x4. Одна клетка этого квадрата остается всегда пустой, так что одну из соседних с ней фишек можно передвинуть на место этой пустой клетки (изменив, тем самым, местоположение пустой клетки). На рис.1а изображены две конфигурации фишек. Рассмотрим задачу перевода начальной (первой) конфигурации в целевую (вторую) конфигурацию. Решением этой задачи будет подходящая последовательность сдвигов фишек, например: «передвинуть фишку 8 вверх, фишку 6 влево и т.д.». Более простым вариантом этой головоломки является квадрат 3x3 и восемь фишек на нем – пример соответствующей задачи показан на рис.5.1б.

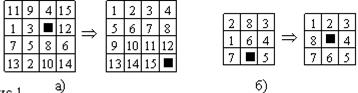
Рис. 5.1. Варианты головоломок

Основными особенностями класса задач, к которому принадлежит рассмотренная головоломка, является наличие в каждой задаче точно определенной начальной ситуации и точно определенной цели. Имеется также некоторое множество операций, или ходов, переводящих одну ситуацию в другую. Именно из таких ходов состоит искомое решение задачи., которое можно в принципе (теоретически) получить методом проб и ошибок. Действительно, отправляясь от начальной ситуации, можно построить все промежуточные конфигурации, возникающие в результате выполнения каждого из возможных ходов, затем построить множество конфигураций после применения следующего хода и так далее – пока не будет достигнут целевая конфигурация.

Ключевым понятием при формализации задачи в пространстве состояний является понятие состояния, характеризующего некоторый момент решения задачи. Например, для игры в пятнадцать состояние – это просто некоторая конкретная конфигурация фишек. Среди всех состояний выделяются начальное состояние и целевое состояние (целевая конфигурация), в совокупности определяющие задачу, которую надо решить.

Другим важным понятием для рассматриваемого представления является понятие оператора, или допустимого хода в задаче. Оператор преобразует одно состояние в другое, являясь по сути функцией, определенной на множестве состояний и принимающей значения из этого множества. Для игры в пятнадцать (или в восемь) удобнее выделить четыре оператора, соответствующие перемещениям пустой клетки влево, вправо, вверх, вниз. В некоторых случаях оператор может оказаться неприменимым к какому-то состоянию: например, операторы вправо и вниз неприменимы, если пустая клетка расположена в правом нижнем углу (соответствующая функция является частично определенной).

В терминах состояний и операторов решение задачи есть определенная последовательность операторов, преобразующая начальное состояние в целевое. Решение задачи ищется в пространстве состояний – множестве состояний, достижимых из начального состояния при помощи операторов. В игре в пятнадцать пространство состояний состоит из всех конфигураций фишек, которые могут быть образованы в результате допустимых перемещений фишек.

Пространство состояний можно представить в виде графа, вершины которого соответствуют состояниям, а дуги – применяемым операторам. Тогда решение задачи – это путь, ведущий от начального состояния к целевому. На рис.5.2 показана часть пространства состояний для игры в пятнадцать, в каждой вершине помещена та конфигурация фишек, которую она представляет. Пространства состояний могут быть большими и даже бесконечными, но в любом случае предполагается конечность множества допустимых операторов и счетность множества возможных состояний.

Итак, формализация задачи с использованием пространства состояний включает выявление и определение следующих составляющих:

формы описания состояний и описание исходной задачи;

множество операторов и их воздействий на описания состояний;

указание свойств целевых состояний (или же явное их задание).

Эти составляющие задают (неявно) пространство, в котором требуется провести поиск решения задачи.

Ясно, что решение задачи, представленной описанным способом, можно в принципе обнаружить, осуществляя последовательный поиск, или перебор вершин, в пространстве состояний. В начале этого процесса к начальному состоянию применяется тот или иной оператор. Затем на каждом шаге поиска к одному из уже полученных (просмотренных) состояний применяется допустимый оператор и строится новая вершина. Поиск заканчивается, когда построено целевое состояние. Заметим, что такой процесс построения вершин пространства состояний означает по сути преобразование в явную форму некоторой части графа, заданного начальным состоянием и операторами, определяющими правила получения новых вершин.

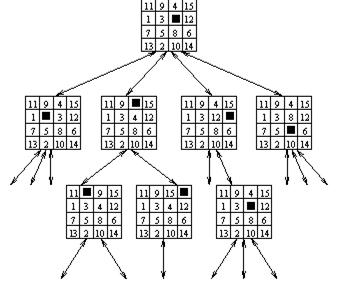
Рис. 5.2. Часть пространства состояний

Рассмотрим дополнительно несколько характерных примеров представления задач в пространстве состояний, к числу которых относится задача об обезьяне и банане. В комнате находятся обезьяна, ящик и связка бананов, которая подвешена к потолку настолько высоко, что обезьяна может до нее дотянуться, только встав на ящик. Нужно найти последовательность действий, которая позволит обезьяне достать бананы. Предполагается, что обезьяна может ходить по комнате, двигать по полу ящик, взбираться на него и схватить бананы.

Описание состояния этой задачи должно включать следующие элементы: местоположение (координаты) обезьяны в комнате – в горизонтальной плоскости пола и по вертикали (на полу обезьяна или на ящике), местоположение ящика на полу и наличие у обезьяны бананов. Эти элементы можно представить в виде четырехэлементного списка (ПолОб, ВертОб, ПолЯщ, Цель), где ПолОб и ПолЯщ – соответственно положение обезьяны и ящика на полу, ВертОб – это П или Я в зависимости от того, где находится обезьяна, на полу или на ящике, а Цель – это 0 или 1 в зависимости от того, достала ли обезьяна бананы или нет.

Операторы в задаче об обезьяне соответствуют четырем ее возможным действиям:

Подойти(X) – переход обезьяны к точке X горизонтальной плоскости пола;

Передвинуть(Y) – передвижение обезьяной ящика в точку Y пола;

Взобраться – обезьяна взбирается на ящик;

Схватить – обезьяна хватает связку бананов.

По сути, для решения задачи значимы лишь три точки:

То - точка первоначального местоположения обезьяны;

Тя - точка первоначального расположения ящика;

Тб - точка, над которой подвешены бананы.

Рассмотрим теперь классическую задачу о коммивояжере. В ней коммивояжер, располагая картой дорог между несколькими городами, должен выстроить маршрут своей поездки так, чтобы побывать в каждом городе, но не более одного раза. На рис.5.3 показана карта дорог между 7 городами.

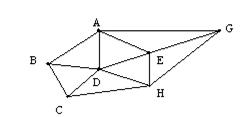
Рис. 5.3. Карта дорог

Получающееся пространство состояний представлено деревом, показанном на рис.5.4.

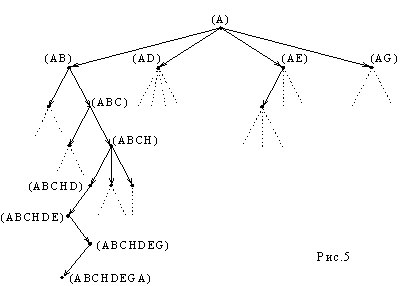
Рис. 5.4. Пространство состояний