
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Лабораторная работа №1
Дата добавления: 2015-10-15; просмотров: 611
|
|
При выполнении вычислений следует всегда руководствоваться практически необходимой точностью. Вести вычисления с точностью большей, чем это допускают данные задачи, бессмысленно.
При округлении руководствуйтесь следующими правилами:
1. Округление достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше, чем 5.
2. Если первая из отбрасываемых цифр больше, чем 5, то последняя цифра увеличивается на единицу. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр - 5, а за ней есть одна или несколько цифр, отличных от нуля. Например, различные округления числа 35.856 будут 35.86; 35.9; 36.
3. Если отбрасываемая цифра равна 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т.е. последняя сохраняемая цифра оставляется неизменной, если она четная, и увеличивается на единицу, если она нечетная. Например, 0.435 округляем до 0.44; 0.465 округляем до 0.46. В этом случае при многочисленных округлениях избыточные числа будут встречаться примерно так же часто, как и недостаточные, т.е. будет иметь место их взаимная компенсация.
Из правил округления имеется существенное исключение: при округлении погрешностей последняя сохраняемая цифра увеличивается на единицу, если старшая отбрасываемая цифра 3 или больше 3.
Имея результаты измерений, можно определить верные, сомнительные и неверные цифры. Разряд сомнительной цифры совпадает с разрядом первой значащей цифры погрешности. Цифры, стоящие слева от сомнительной, называют верными, а стоящие справа от сомнительной - неверными. Неверные цифры должны быть отброшены как в исходных данных, так и в окончательном результате расчета.
При округлении пользуются понятием о значащих цифрах. Все цифры числа, начиная с первой слева, отличной от нуля, до последней (может быть и нуль), называются значащими цифрами. К значащим цифрам относятся все верные и сомнительные цифры. К незначащим цифрам относятся: 1) нули в начале числа, определяющие разряды десятичных дробей в числах, меньших единицы; 2) нули в конце числа, заменившие цифры, отброшенные после округления; 3) неверные цифры, если они по каким-либо причинам не отброшены.
Например, числа 0.002583 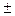 0.00003, 0.0258
0.00003, 0.0258 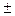 0.0002, 258
0.0002, 258 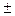 2 содержат по 3 значащие цифры. В числе 2547 все числа значащие, так как ошибка не указана.
2 содержат по 3 значащие цифры. В числе 2547 все числа значащие, так как ошибка не указана.
При сложении и вычитании округление всех чисел производится по правилам 1-3 до разряда на единицу меньшего, чем разряд наименее точного числа. В результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков:
23.2 + 0.442 + 7.247 »23.2 + 0.44 + 7.25 = 30.89 » 30.9.
При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр:
30.9 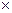 1.8394 » 30.9
1.8394 » 30.9 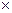 1.84 = 56.856 » 56.9,
1.84 = 56.856 » 56.9,
56.9 : 2.412 » 56.9 : 2.41 = 23.609 » 23.6.
При возведении в степень в результате следует сохранять столько значащих цифр, сколькоих имеет возводимое в степень приближенное число:
(11.38)2 = 129.5044 » 129.5.
| |
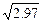 =1.724 » 1.72 .
=1.724 » 1.72 .
При нахождении логарифма приближенного числа нужно брать из таблиц столько знаков, сколько верных знаков содержит данное число:
lg77.23 » 2.8878 » 2.888 .
Примечание. При вычислении промежуточных результатов следует брать на одну цифру больше, чем указано в округлении при выполнении математических действий над числами. В окончательном результате эта "запасная" цифра отбрасывается. Приведенный ниже пример поясняет сказанное:

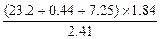


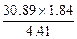

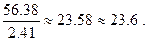
Значение физической величины округляется до первой сомнительной цифры. Все цифры, стоящие после сомнительной, отбрасываются. Абсолютная ошибка округляется до одной значащей цифры, относительная ошибка - до двух значащих цифр.
Пример. Путем измерений и математических расчетов было получено, что для объема некоторого тела имеют место следующие числа (см. с. 13: Вычисление абсолютной и относительной ошибок измерений):
V = 43.235 м3; DV = ± 0.423 м3.
Оказалось, что сомнительной цифрой при вычислении объема является 2. Тогда результат можно записать в следующем виде:
V= (43.2 ± 0.4) м3; EV = 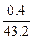
 100% = 0.92%.
100% = 0.92%.
Промахи, систематические и случайные погрешности измерений
Истинное значение физической величины абсолютно точно определить нельзя. Измерение тел, предметов или любой физической величины всегда производится с той или иной степенью точности[1], т.е. с той или иной степенью приближения к истинному значению искомой величины. Если указываем, что высота дерева 2 м 56 см, а измерена она с точностью до 1 см, то это будет означать, что отклонение найденной высоты от истинной не превышает 1 см.
При измерении физических величин под действием самых разнообразных причин возникают погрешности измерения. Все погрешности принято подразделять на систематические, случайные и промахи (ошибки).
| <== предыдущая лекция | | | следующая лекция ==> |
| Техніка безпеки при експлуатації теплообмінних апаратів і установок | | | Дослідження нелінійного електричного кола змінного струму |