Глава 3. Функціонування єдиної державної системи цивільного захисту

Дата добавления: 2015-10-15; просмотров: 533

Регресійний аналіз вивчає вплив на значення досліджуваної (залежної) змінної значень однієї або кількох незалежних змінних.

Кореляційний аналіз досліджує характер і ступінь взаємозалежності факторів, які впливають на досліджувану змінну. Результати регресійно-кореляційного аналізу використовують для прогнозування найімовірнішого значення досліджуваної змінної для різних значень факторів, які на неї впливають.

На практиці регресійно-кореляційний аналіз полягає в пошуку (методами математичної статистики) оцінок числових характеристик системи випадкових величин. Тому він потребує ґрунтовного ознайомлення з основними поняттями теорії ймовірності.

Предмет теорії ймовірності — це специфічні закономірності масових однорідних випадкових явищ.

Випадковим називають явище, яке при неодноразовому відтворенні одного й того самого досліду (за незмінних основних найвпливовіших умов) відбувається кожного разу дещо по-іншому (через вплив багатьох другорядних факторів).

Елементарна подія — це можливий результат досліду, подія — це довільна підмножина множини елементарних подій.

Імовірність події - це чисельна міра об'єктивної можливості виникнення події (тобто однієї з її елементарних подій) у результаті досліду.

Відносна частота ймовірної події — це частота виникнення події в серії дослідів.

Безпосереднє обчислення ймовірності (виходячи з умов досліду, що відзначається симетрією через об'єктивно однакову можливість усіх випадків) можливе тільки для так званої схеми випадків, коли групі подій притаманні одночасно три властивості: утворюють повну групу подій, несумісні в кожному досліді й рівноможливі.

Випадок називають сприятливим для події, якщо його поява спричинює появу цієї події.

Тільки для "схеми випадків" правильним є "класичне" позначення ймовірності події А через Р(А)= т/п, тобто як відношення кількості сприятливих для події А випадків до загальної кількості всіх випадків.

Випадкова величина (далі в.в.) — це функція, яка кожній елементарній події ставить у відповідність деяке число. Розрізняють в.в. дискретні (набувають значення лише з деякої зліченної множини) та неперервні (можуть набувати будь-якого значення з інтервалу значень).

Закон розподілу в.в. встановлює зв'язок між можливими значеннями в.в. і відповідними їм ймовірностями.

Закон розподілу дискретної в.в. А найкраще описувати рядом розподілу, який у табличній формі задає ймовірність Р(Х = х_п) =р_п того, що X= х_п. При цьому р₁ + ... +р_п = 1. Графічну версію ряду розподілу називають многокутником розподілу.

Для опису закону розподілу неперервної в.в. використовують функцію розподілу. Функція розподілу F задається співвідношенням F(x) = P(X<x).

Якщо функція розподілу диференційована, то для опису розподілу зручніше використовувати щільність розподілу f. Щільність розподілу — це перша похідна функції розподілу, f(x)=F'(x). Графік щільності розподілу називають кривою розподілу.

Наведені форми запису закону розподілу вичерпно характеризують в.в. На жаль, на практиці отримати ці форми дуже важко, як правило, навіть неможливо. Тому зазвичай шукають лише числові характеристики розподілу, які визначають його найістотніші особливості.

Найвідоміші такі числові характеристики;

• математичне сподівання т_х — зважене ймовірностями середнє значення в.в.;

• мода Mod — найімовірніше значення в.в. X;

• медіана Med — значення в.в. X, для якого Р(Х < Med) = Р(Х >> Med);

• дисперсія D_x;

• середпьоквадратичне відхилення _х;

• початкові v_x і центральні m_х моменти k:-го порядку.Математичне сподівання т_х в.в. Xрозраховують за формулами:

т_х =М[Х] = x₁p₁ + ... + х_пр_п для дискретної в.в.;

для неперервної в.в.

Центрована випадкова величина — це різниця між в.в. X та її математичним сподіванням m (тобто X_c = X - m_x); вона описує розподіл відхилень в.в. від її сподіваного значення.

Дисперсія D_x в.в. X— це математичне сподівання квадрата її центрованої в.в., тобто

D_x = D[X] = М[X_С²] = М[(Х - т_x)²] =M[Х²] - т²_x.;

Середньоквадратичне (стандартне) відхилення а — це квадратний корінь з дисперсії (D_x)^1/2. При цьому Середньоквадратичне відхилення має розмірність в.в. і є зручнішим для опису розсіювання значень навколо математичного сподівання, ніж дисперсія.

Початковий момент V_x k-ro порядку в.в. X—це математичне сподівання k-го степеня цієї в.в., тобто

v_x = M[X^k]=x₁^kp₁+...+ x_n^kp_k, або

Центральний момент μ_x k-го порядку в.в. X— це математичне сподівання k-то степеня її центрованої в.в., тобто

μ_x= М[(X_c)^k] = M[(Х-m_x)^k] = (x₁ -m₁)^kp₁ +... + (х_n -m_n)^kp_n, або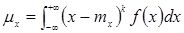

Можна показати, що

v₁=m_x,

μ₁=m_x,

μ₂=v₂-v₁²=D_x,

μ₃=v₃-3v₂v₁+2v₁³=S_xσ³ (де S_x=μ₃/σ³ -асиметрія розподілу),

μ₄=v₄-4v₃v₁+6v₂v₁²-3v₁⁴=E_x=(μ₄/σ⁴) -3 (де Е_х — ексцec розподілу).

Якщо результат досліду описується кількома в.в., то кажуть про систему випадкових величин. Властивості системи в.в. залежать не тільки від властивостей її складових, а й від можливого взаємозв'язку між ними.

Випадкові величини системи в.в. можуть бути або зовсім незалежні, або цілком (математично або функціонально) залежні, або мати імовірнісну (стохастичну) залежність.

Систему двох в.в. позначають (X,Y) і зображують на площині випадковою точкою або випадковим вектором.

Функцію розподілу системи двох в.в. (X, Y) позначають F(x,y), a щільність розподілу системи розраховують за формулою f(x,y)=(F'_х)'_у(х,у) =f₁(x)f(y|x), де f₁(x) — щільність розподілу в.в. X; f(y|x) -умовна щільність розподілу в.в. У за умови, що в.в. X набула значення X,

Випадкову величину Г називають незалежною від X, якщо умовна щільність не залежить від значення X, тобто f(y|x) =f₂(y), де f₂(у) -щільність розподілу в.в. Y. Для незалежної в.в. f(x,y) =f₁(x)f₂(y).

Кореляційний момент (коваріація) — це математичне сподівання добутку центрованих величин К = μ_1,1 = M[X_CY_c] = М[(Х-m_x)(Y-m_y)]. Недолік коваріації K_xy полягає в тому, що вона характеризує рівень взаємозалежності в.в. та їх розсіяння в сукупності. Отже, інформацію про рівень взаємозалежності з коваріації безпосередньо виділити неможливо. Тому використовують іншу характеристику — коефіцієнт кореляції.

Коефіцієнт кореляції характеризує рівень лінійної залежності двох в.в. і обчислюється за формулою r_xy=К_xy/(σ_xσ_y), де σ_x, σ_y — се-редньоквадратичні відхилення. Для незалежних в.в. системи К_xy = 0 і r_xy =0. Зазвичай -1≤r_xy≤+1 і тільки при точній лінійній залежності . Кореляція є додатною (r_xy> 0) або від'ємною (r_хy < 0), якщо при збільшенні однієї в.в. інша має тенденцію відповідно до збільшення або зменшення.

Наявність істотної кореляції і функціональну форму кореляції бачимо з графіка розподілу випадкових точок.

Однопараметрична лінійна регресія описується рівнянням Y = аХ +b.

Якщо досліджувана змінна в.в. К залежить від кількох незалежних змінних в.в. Х_i, маємо багатопараметричну лінійну регресію з рівнянням типу Y = a₁X₁ + а₂Х₂ + ...+ а_пХ_п + b.

Нелінійна регресія (нелінійна залежність досліджуваної змінної від однієї або кількох незалежних змінних) може бути:

• поліноміальною (у=b + с₁х + с₂х² + с₃х³ + ... + с_бх⁶);

• логарифмічною (у = сlnх + b);

• експоненціальною (у = се^bx);

• періодичною (у = nsinx).

Закон розподілу системи в.в. (у будь-якій формі) є вичерпним імовірнісним описом системи. Проте в перелічених далі випадках:

• недостатньо статистичного матеріалу,

• невиправдана важкість пошуку закону через невисокі вимоги до точності результатів,

• тип закону наперед відомий, а потрібні деякі параметри використовують приблизний опис системи в.в. за допомогою мінімальної кількості таких числових характеристик:

• п математичних очікувань (які характеризують середні значення в.в.) m₁, m₂,...,m_n;

• п дисперсій (які характеризують розсіяння в.в.) D₁,D₂-.., D_n;

• п(п - 1) кореляційних моментів (які характеризують попарну кореляцію всіх величин системи) K_ij = M[(X_c)_i(X_c)_j] =M[(X_i-m_i)(X_j-m_j)].

При цьому кореляційні моменти зручно розміщувати у вигляді прямокутної кореляційної матриці, на головній діагоналі якої розміщуються дисперсії. Через симетрію елементів матриці відносно головної діагоналі, як правило, заповнюють лише її верхню половину. Для некорельованих величин усі елементи кореляційної матриці (крім дисперсій у головній діагоналі) дорівнюють нулю.

Для п величин кореляційна матриця має такий вигляд:

для двох величин

Якщо потрібно знайти лише числові характеристики функції від випадкових величин (аргументів) за відомими числовими характеристиками аргументів, використовують такі співвідношення:

М[с] = 0; М[сХ] = сМ[Х]; М[Х + У]=M[Х] + М[У], D[c] = 0; D[cX] = C²D[X]; D[X+Y] = D[X] + D[Y] + 2K_xy.

Якщо Y = a₁X₁ +... +a_nX_n+b, то M[У]=а₁М[Х₁] +... + a_nM[X_n]+b, D[Y] = a₁²D[X₁] + ... + a_n²D[X_n] + 2S_i<ja_ia_jK_ij,

Точковою оцінкою параметра в математичній статистиці називають приблизне значення параметра, обчислене на основі обмеженої кількості дослідів. Бажано, щоб точкова оцінка була змістовною, ефективною і незміщеною. Наприклад, для дисперсії незміщена оцінка для вибірки (в Excel її повертає статистична функція ДИСП) і статистична оцінка для генеральної сукупності (в Excel її повертає статистична функція ДИСПР) задовольняють рівняння D_в=D_стn/(n-1).