Text Messaging Abbreviations

Дата добавления: 2015-10-18; просмотров: 448

В основе модели находится Булева логика, т.е. используются операции дизъюнкции и конъюнкции. Набор базовых эелемнтов:

L={T,P,A,F}

L – логическая модель;

T – множество терминальных (атомных )элементов, т.е. не подлежащих дальнейшему делению.

P – множество синтаксических правил, позволяющих стоить из множества Т элементов правильные выражения.

A – множество аксиом, т.е. априорно истинных выражений.

F – множество семантических правил, позволяющих расширить множество аксиом за счет новых выражений.

Пусть m –множество понятий и объектов предметной области. К- множество классов данного объекта, Мк – множество понятий разделенных на мно-во объектов опред-го К-класса.

Каждому классу ставиться в соответствие характеристическая функция представляя-я собой предикат.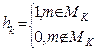

Проверяем на принадлежность. Вводится понятие предиката признака, которому ставиться в соответствие определенное св-во понятия или объекта.

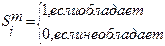
Каждому объекту m- ставится в соответствие его логическое описание, пред-т собой конъюнкцию всех предикатов признаков данного объекта.

Для описания множ-ва объектов принадлежащих классу, вводится понятие Аксиомы класса Ак- дизъюнкция по j всех логических описаний:

В идеальном случае при построении полного и непротиворечивого описания класса аксиома A_к д.б. равна характеристической функции (A_к=h_k), таким образом формируется система понятий о предметной области на основе создания аксиом.

35. (Продолжение)

Для сокращения размерности аксиом в процессе обучения логической системы стоится оптимальное решающее правило: при построении коньюкции следующим выбирается предикат-признак, который максимизирует апостериорную вероятность того, что объект принадлежит данному классу.

Оптимальное решающее правило может быть представлено в виде бинарного дерева, в вершине которого находится признак с максимальной апостериорной вероятностью, а заканчивается дерево листьями, где указывает номер класса.