Вид та розмір стипендій

Дата добавления: 2015-10-19; просмотров: 432

Среди показателей, характеризующих статистические совокупности, важное месте занимают средние величины.

Средняя величина – это показатель, который дает обобщенную (усредненную) характеристику единиц изучаемой совокупности. В средней величине отражается то общее, что имеется в каждой единице совокупности. Сущность статистической обработки методом средней величины заключается в замене индивидуальных значений признака их средним показателем. При этом общий объем изучаемой совокупности остается неизменным.

Пример: есть данные о выработке пяти рабочих: 135, 141, 153, 159, 162.

.

Основные положения теории средних величин

1. Индивидуальные величины, из которых определяется средняя, должны относиться к однородной совокупности и число их должно быть значительным.

2. Метод средней величины должен сочетаться с методом группировки, т.е. необходимо исходную разнородную совокупность разбить на качественно однородные группы.

3. Необходимо вычисление групповых и общих средних величин для объективной оценки изучаемой совокупности.

Средняя арифметическая простая и взвешенная.

Свойства средних величинОшибка! Закладка не определена.

Чаще всего в статистике и социально-экономических исследованиях употребляется арифметическая величина.

Средняя арифметическая простая рассчитывается в случаях, когда значения признака повторяются один или одинаковое число раз в ряде распределения.

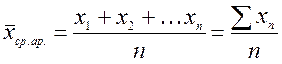(4.1)

где – х _ср.ар. - средняя арифметическая простая; n – количество единиц совокупности.