Технічні характеристики

Дата добавления: 2014-12-06; просмотров: 648

Системы уравнений динамики, как правило, являются существенно нелинейными, и аналитическое решение их в общем виде невозможно. Поэтому в зависимости от специфики задач проводятся упрощения, направленные на исключение отдельных связей, накладываемых уравнениями и краевыми условиями. При этом должны сохраняться существенные черты процесса.

Наиболее простой (в смысле математического решения) является статическая задача. Производные по времени и координатам равны 0, и система дифференциальных уравнений сводится к алгебраической (стационарные режимы объектов с сосредоточенными параметрами).

Следующей по сложности является стационарная задача. Для математического описания нестационарных режимов объектов с сосредоточенными параметрами, а также стационарных режимов объектов с распределенными параметрами по одной пространственной координате обычно используют обыкновенные дифференциальные уравнения. В первом случае независимой координатой является время, во втором – пространственная координата.

Одним из способов упрощения системы уравнений является снижение числа пространственных координат: трехмерную задачу сводим к двумерной или одномерной. При снижении размерности пространства система будет незамкнута, надо использовать алгебраические зависимости, отражающие реальную трехмерность потока. Это большей частью эмпирические зависимости от параметров потока таких величин, как коэффициенты трения, теплоотдачи, скольжения фаз и т.д.

В одномерных моделях параметры изменяются лишь вдоль одной координаты, направленной вдоль оси потока. По сечению канала параметры постоянны и равны среднему значению.

Для одномерного течения жидкости (газа) уравнение сохранения вещества (пространственную координату обозначим z):

(2.2.1)

Для несжимаемых сред, для которых плотность не зависит от времени и постоянна, в (2.1.3) пропадает член и, следовательно, будет .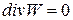

Представление теплообменников в виде одномерных систем приводит к тому, что механизм передачи тепла или вещества вдоль другой координаты оказывается скрытым.

Во-первых, исключается уравнение теплопроводности, то есть градиент температуры по радиусу равен 0 как в оболочке, так и жидкости. Иными словами принимается, что температура на границе «оболочка - жидкость» меняется скачком от температуры стенки до температуры теплоносителя 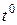. Значит, уравнение теплопроводности заменяется уравнением теплового баланса, записанного для оболочки:

(2.2.5)

где – вес материала погонного метра оболочки канала.

Посылка о нулевом термическом сопротивлении стенки тем меньше искажает результаты, чем тоньше стенка и чем больше коэффициент теплопроводности.

Отказ от рассмотрения механизма передачи тепла в пристенном слое привел к необходимости введения в систему уравнений эмпирического закона теплообмена:

(2.2.6)

где – температура внутренней поверхности оболочки, – коэффициент теплоотдачи, зависящий от параметров потока, условий теплообмена и геометрических размеров канала:

(2.2.7)

Это уравнение вместе с уравнением теплового баланса дает

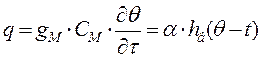(2.2.8)

Во-вторых, исключается механизм вязкого трения, что приводит к вводу в (2.2.4) эмпирической зависимости, характеризующей сопротивление движению в канале:

(2.2.9)

Коэффициент сопротивления трения λ_тр зависит от параметров потока и относительной шероховатости канала. Во многих случаях

(2.2.10)

В-третьих, в систему уравнений вводятся другие эмпирические зависимости, определяющие коэффициенты теплоотдачи, трения, распределения фаз по сечению и др.:

(2.2.11)

Эти эмпирические зависимости получают обычно в стационарных условиях. При их использовании, следовательно, предполагается , что они остаются верными и при нестационарных режимах. При невысоких частотах процесса это является оправданным.

Система уравнений дополняется уравнением состояния теплоносителей:

(2.2.12)

Система полученных уравнений и замыкающих их зависимостей все же остается очень широкой и позволяет решать две большие группы задач: а) исследование устойчивости движения теплоносителя в парогенерирующих каналах; б) исследование динамических характеристик теплообменников.

Первая задача более сложная и требует для своего описания полной системы уравнений; вторая задача – проще, так как при ее решении можно отказаться от рассмотрения уравнения движения.

Исключение уравнения движения означает, что в динамических задачах не учитываются эффекты, связанные с существованием перепада давления вдоль пространственной координаты. Следовательно, по отношению к давлению система рассматривается как сосредоточенная, в которой изменение давления по времени проявляется в качестве внешнего возмущения. Условие постоянства давления вдоль пространственной координаты не приводит к заметной ошибке во всех случаях, когда изменение давления по длине мало по сравнению с абсолютным давлением.

Упрощение математической формулировки нестационарных задач достигается также за счет сокращения числа взаимодействующих систем, уменьшения количества уравнений, исключения некоторых связей в отдельных уравнениях,

Всякое исключение какого-либо дифференциального уравнения снижает порядок системы. То есть с математической точки зрения система оказывается незамкнутой. Исключенное уравнение необходимо заменить алгебраической зависимостью, приближенно отражающей ход процесса. Например, соответствующие параметры могут быть приняты постоянными.

Во многих практических случаях закономерности движения реального потока находятся на основе экспериментальных данных. При экспериментальном исследовании определяются некоторые коэффициенты, так или иначе отражающие реальную структуру потока, то есть распределения скорости, температуры, плотности и другие параметры. Это коэффициенты трения, теплоотдачи, относительные скорости фаз в двухкомпонентных смесях и т.д. Все они представляют собой интегральные характеристики потока, которые с определенным приближением отражают обмен количеством движения, теплотой, веществом, существующий в реальном потоке. С помощью указанных коэффициентов и усредненных по сечению потока параметров, выражаются передача теплоты, гидравлическое сопротивление, распределение фаз. Связи между ними также находится из опыта.

Использование эмпирических коэффициентов и упомянутых зависимостей позволяет отказаться от учета реальной трехмерности потока и одни уравнения упростить, а другие – исключить совсем. Такие упрощения допустимы, так как эмпирические зависимости в определенной мере отражают реальную трехмерность потока. В результате указанных посылок для расчета динамических характеристик можно использовать одномерную модель, а в некоторых случаях – и модель с сосредоточенными параметрами.

Система уравнений дополняется уравнением состояния F(p, v, T) =0 и эмпирическим зависимостями.

При наличии двух движущихся сред система уравнений дополняется такой же, но отнесенной ко второй движущейся среде.

В моделях с сосредоточенными параметрами все параметры системы не зависят от пространственных координат и являются лишь функциями времени. Производные по пространственной координате заменяются отношением разности значений функций между входом и выходом к полной длине канала. Для описания процессов в таких объектах известные законы сохранения обычно записываются в форме уравнений баланса (массы, энергии, движения).

Уравнение сохранения вещества:

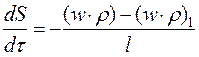(2.2.13)

Умножив на длину и сечение канала, получим:

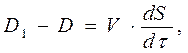(2.2.14)

где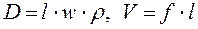

Уравнение сохранения энергии:

(2.2.15)

(2.2.16)

Если ось координат направлена вдоль оси движения жидкости, то уравнение сохранения количества движения

(2.2.17)

где – масса системы;

– сила давления;

– сила трения.

В устойчивых системах переходные процессы протекают одинаково во всех однотипных параллельно включенных элементах. Это дает возможность при исследовании переходных процессов рассматривать не всю систему в целом, а один из элементов. Например, при исследовании динамики многоканальных теплообменников рассматривать движение в одном канале.