Протокол. Витяг з протоколу.

Дата добавления: 2015-10-19; просмотров: 564

При дифракции на щели, дифракционное распределение интенсивности, соответствующее в математике квадрату Фурье-преобразования от прямоугольного импульса, с точностью до постоянного множителя описывается выражением

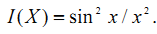
Щелевое отверстие имеет одну плоскость симметрии. Распределение интенсивности в ДК

от щелевого отверстия представляет произведение квадрата функции синуса на

функцию, определяющую скорость спада интенсивности в ДК. Так как функция синуса уже является периодической, то получению трансляции спектра в ДК нам “мешает” только

затухание дифракционного спектра и различие линейных размеров центрального дифракционного лепестка и боковых.

Дифракционные волны, возникающие при дифракции на плоских апертурах, в соответствии с ГТД порождаются или гладкими участками контура или точками излома (угловыми точками) контура. Угловые точки контура излучают сферические волны, существующие на всей плоскости ДК, а краевые дифракционные волны, как правило, имеют ограниченную область существования. Исключением можно считать тороидальную волну, излучаемую апертурой круглой или

эллиптической формы. В соответствии с ГТД линии структуры в этом случае образуются в результате интерференции двух точечных “скользящих” по окружности источников. Линии минимумов ДК апертур круглой или эллиптической формы представляют систему концентрических колец круглой или эллиптической формы (рис. 2.11). Такая система концентрических окружностей и эллипсов обладает трансляционной симметрией подобия.

Учитывая механизм построения плоской сетки сетчатого орнамента, а также области существования дифракционных волн, для наблюдения трансляционной симметрии в ДК наиболее подходит модель попарной интерференции излучения точечных источников. В случае круглого отверстия таких источников всего два. В силу осевой симметрии бесконечного порядка они образуют систему концентрических окружностей. Для многоугольного контура число таких источников уже больше двух и они являются фиксированными.

Минимальное число таких источников для прямоугольной апертуры – четыре.

Распределение интенсивности в интерференционной картине двух фиксированных точечных источников представляет систему эквидистантных полос. Пересечение систем полос должно образовать сетчатый орнамент.

Трансляционная симметрия дифракционной картины от совокупности прямоугольных элементов. Преобразование ДК путем ее умножения на функцию, обратную затуханию, приводит к появлению трансляционной симметрии, и мы получаем бордюр с одной осью переносов и периодом трансляции, равным π. В радиотехнике такому преобразованию частотного спектра соответствует операция дифференцирования исходного сигнала. Это

преобразование используется и при оптической обработке информации. На практике такое преобразование можно выполнить, используя различные пространственные фильтры.

Распределение интенсивности от прямоугольного отверстия со сторонами 2a и 2b с точностью до постоянного множителя имеет вид

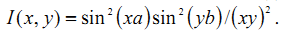Преобразовав спектр прямоугольного отверстия

аналогичным образом, т.е. умножив его на 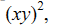получим распределение интенсивности,

соответствующее плоской сетке (рис. 2.12).

Элементом трансляции здесь является прямоугольный участок ДК со сторонами π/a, π/b.

С точки зрения ГТД ДК прямоугольного отверстия формируется краевыми волнами и излучением из угловых точек и состоит из двух основных характерных областей – области интерференции краевых волн и области интерференции точечных источников, соответствующих излучению из угловых точек контура. Причем эти области сильно различаются по интенсивности. Интенсивность в области ДК, соответствующей излучению угловых точек, спадает очень быстро (1/x2y2), а область краевых волн – (1/xy). ДК от многоугольной апертуры имеет такой же характер, как и от прямоугольной апертуры, но только в том случае, если ее можно представить в виде совокупности параллелограммных апертур.

Процесс формирования дифракционного поля многоугольной апертуры можно представить несколькими способами: как дифракционное поле, создаваемое точечными источниками, расположенными в пределах всей апертуры; как дифракционное поле, образованное суммой излучения граней; как дифракционное поле, образованное суммой излучения вершин

многоугольника. касается симметрии трансляционной, то, согласно ГТД, она

возникает в зонах влияния волн угловых точек.