Лабораторний практикум побудови синтаксичних аналізаторів.

Дата добавления: 2015-10-19; просмотров: 621

o Многогранник называется правильным, если все его грани - _________ правильные многоугольники, а все многогранные ________ имеют одинаковое число граней.

o Площадь _________ поверхности прямой призмы равна ___________ периметра основания на высоту призмы.

o Пирамида — ___________, у которого одна грань n-угольник — основание пирамиды, а остальные __________ грани — треугольники с общей вершиной — вершиной пирамиды.

Задание 2 Определите вид многогранника по рисунку.

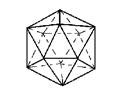
а) б) в)

№25 Тема: Виды многогранников.

Цель:

• Продолжить формирование умений к созданию моделей пространственных фигур.

Задание. Выполнить упражнения № 271 – 275 по вариантам на стр. 72, используя иллюстрации на стр. 72 рис. 88-92.

№26 Тема: Площадь боковой и полной поверхностей многогранников.

Цель:

• Продолжить формирование умения и навыки решения геометрических задач.

Задание 1. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями 6 см и 8 см и боковым ребром 10 см.

Задание 2. Найдите площадь боковой поверхности правильной четырёхугольной пирамиды, сторона основания которой равна 6 см и высота равна 4 см.

Задание 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите площадь поверхности данной призмы.

№27 Тема: Градусное и радианное измерение углов.

Цель: Продолжить формирования навыка нахождения градусной и радианной мер углов.

Теория:

Градусная мера. Здесь единицей измерения является градус (обозначение) – это поворот луча на 1/360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°. Один градус состоит из 60 минут (их обозначение ‘ ); одна минута – соответственно из 60 секунд (обозначаются “ ).

Радианная мера. Как мы знаем из планиметрии, длина дуги l, радиус r и соответствующий центральный угол связаны соотношением:

= l / r .

Эта формула лежит в основе определения радианной меры измерения углов. Так, если l = r , то = 1, и мы говорим, что угол равен 1 радиану, что обозначается: = 1 рад. Таким образом, мы имеем следующее определение радианной меры измерения:

Радиан есть центральный угол, у которого длина дуги и радиус равны (AmB = AO, рис.5 ). Итак, радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги.

Рис. 5 Единичная окружность.

Следуя этой формуле, длину окружности C и её радиус r можно выразить следующим образом:

2 = C / r .

Так, полный оборот, равный 360° в градусном измерении, соответствует2 в радианном измерении. Откуда мы получаем значение одного радиана:

Обратно,

Задание 1. Пользуясь калькулятором и формулой перехода от градусной меры угла к радианной, найти радианную меру углов:

1) 1°; 5°; 18°; 30°; —135°; 225°; —162°;

2) 50°; 42°30'; 22°10'; 70°15'.

Задание 2. Пользуясь формулой перехода от радианной меры угла к градусной, найти градусную меру угла, радианная мера которой равна:

1) 0,5π; —0,75π; ^π/₃; 0,1π; — ^2π/₁₅; ^5π/₆; — ^7π/₁₂ ;
2) 1; 2;—3; 2,5; 0,1; 0,01;—2,1; —0,55.

Задание 3. Пользуясь таблицей для перевода радианной меры угла (дуги) в градусную, определить градусную меру углов (дуг): 0,54 рад; 3,83 рад; 2,106 рад; 3,512 рад; 12,378 рад.

Задание 4. Определить длину дуги окружности радиуса R = 25 см, если:

1) радианная мера дуги равна 1,25 рад;

2) градусная мера дуги равна 144°.

Задание 5 Шкив скоростного электромотора делает 120 000 оборотов в минуту. Определить угловую скорость вращения этого шкива: 1) в град/сек; 2) в рад/сек.

№28 Тема: Определения тригонометрических функций.

Цель:

• Продолжить формирование умений выделять из текста главное.
• Продолжить формирование умений к систематизации и анализу текста учебника.

Задание. Составить конспект по плану на тему «Тригонометрические функции» на стр. 124-128, 133-135 учебник Алгебра и начала анализа 10-11 класс Ш.А. Алимов и др.

При написании конспекта рекомендуется следующая последовательность:

4. проанализировать содержание каждого фрагмента текста, выделяя относительно самостоятельные по смыслу;

5. выделить из каждой части основную информацию, убрав избыточную;

6. записать всю важную для последующего восстановления информацию своими словами или цитируя, используя сокращения.

План конспекта:

1. Определения синуса, косинуса, тангенса и котангенса.

2. Основные тригонометрические тождества.

3. Зависимость между синусом, косинусом и тангенсом одного и того же угла.

№29 Тема: Преобразование тригонометрических выражений.

Цель:

• Продолжить формирование умений выделять из текста главное.
• Продолжить формирование умений к систематизации и анализу текста учебника.

Задание 1. Подготовить ответы на вопросы:

1. Определение радианной меры угла;

2. Определение единичной окружности;

3. Определение косинуса;

4. Определение синуса;

5. Определение тангенса;

6. Определение котангенса.

7.

Задание 2. Вставьте недостающие части в тригонометрические формулы:

а)

б)

в)

г)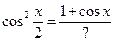

д)

е)

ж)

з)

№30 Тема Функция синус, косинус и их свойства.

Цель:

• Продолжить формирование навыков построение таблицы значений функции.
• Продолжить формирование умений построения графика функции.

Задание Построение графика тригонометрической функции и провести исследование по схеме указанной в приложении 2:

1. y=1+cosx;

2. y=1-sinx;

3. y=tg2x;

4. y=tg(x+π).

Схема исследования тригонометрической функций на примере y=sin x:

1. Область определения: D (sin x) = R .

2. Множество значений: E (sin x) = [ –1; 1 ] .

3. Четность, нечетность: функция нечетная.

4. Периодичность: функция периодическая с основным периодом T=2π.

5. Нули функции: sin x = 0 при x = πn, n Z.

6. Промежутки знакопостоянства:
; .

7. Промежутки монотонности:
;
.

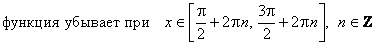8. Экстремумы:
; .

9. График функции y= sin x изображен на рисунке.

№31 Тема: Периодичность, четность тригонометрических функций.

Цель: Продолжить формирование умения и навыки решения тригонометрических задач.

Задание 1. Выяснить, какие из данных функций являются четными и какие нечетными:

1) у = sin (—х); 4) у = sin x cos х; 7) у = sin²x;

2) у = cos (—х); 5) у = cos²x;

3) у = tg (2х); 6) у = sin x + tg x.

Задание 2. Найдите наименьший положительный период каждой из функций:

а) 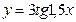; б) .

№32 Тема: Графики тригонометрических функций.

Задание. Составить конспект по плану на тему «Тригонометрические функции» на стр. 46-58 учебник Математика 11 класс М.И. Башмаков.

При написании конспекта рекомендуется следующая последовательность:

7. проанализировать содержание каждого фрагмента текста, выделяя относительно самостоятельные по смыслу;

8. выделить из каждой части основную информацию, убрав избыточную;

9. записать всю важную для последующего восстановления информацию своими словами или цитируя, используя сокращения.

План конспекта:

4. Основные понятия.

5. Синус и косинус.

a. Основные свойства функций.

b. График функций.

6. Тангенс и котангенс.

a. Основные свойства функций.

b. График функций.

№33 Тема: Простейшие тригонометрические уравнения.

Цель:

· Продолжить формирование навыков решения тригонометрических уравнений.

Формулы:

1. Общий вид решения уравнения cos x = a, где | a | £ 1, определяется формулой:

x = ± arccos(a) + 2pk, k Î Z (целые числа),

2. Общий вид решения уравнения sin x = a, где | a | ≤ 1, определяется формулой:

x = (- 1)^k · arcsin(a) + k, k ÎZ (целые числа),

3. Общий вид решения уравнения tg x = a определяется формулой:

x = arctg(a) + k, kÎ Z (целые числа).

4. Общий вид решения уравнения ctg x = a определяется формулой:

x = arcctg(a) + k, kÎZ (целые числа).

Задание. Решить тригонометрические уравнения:

№34 Тема: Решение тригонометрических неравенств.

Цель:

· Продолжить формирование навыков решения тригонометрических неравенств.

Задание Решить тригонометрические неравенства на интервале :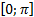

а)

б)

в)

г)

№35 Тема: Тригонометрические функции в жизни.

Цель работы: Сформировать навык поиска, анализа, систематизации материала по теме, а также овладеть умением последовательно, логично и аргументировано излагать в устной форме полученные знания, выражать собственную позицию и подтверждать её доказательствами и рассуждениями научно характера.

ЗаданиеПодготовить сообщение на тему «Тригонометрические функции в жизни» или «Тригонометрические функции в профессиональной деятельности».

№36 Тема: Тела вращения.

Цель работы: Сформировать навык поиска, анализа, систематизации материала по теме, а также овладеть умением последовательно, логично и аргументировано излагать в устной форме полученные знания, выражать собственную позицию и подтверждать её доказательствами и рассуждениями научно характера.

ЗаданиеПодготовить сообщение на тему «Тела вращения в моей профессиональной деятельности» (см. ПРИЛОЖЕНИЕ 3).

№37 Тема: Цилиндр.

Цель: Продолжить формирование навыков решения геометрических задач.

Задание 1. Сколько квадратных метров листовой жести пойдет для изготовления трубы длинной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади ее боковой поверхности?

Задание 2. Площадь осевого сечения цилиндра равна 10 м², а площадь основания – 5 м². Найдите высоту цилиндра.

№38 Тема: Конус.

Цель: Продолжить формирование навыков решения геометрических задач.

Задание 1. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.

Задание 2. Ведро имеет форму усеченного конуса, радиусы оснований которого ровны 15 см и 10 см, а образующая равна 30 см. Сколько килограммов краски нужно взять для того, чтобы покрасить с обеих сторон 100 таких ведер, если на 1 м² требуется 150 г краски? (Толщину стенок в расчет не принимать.)

№39 Тема: Шар.

Цель: Продолжить формирование навыков решения геометрических задач.

Задание 1. Найти площадь сферы, радиус которой равен: а) 6 см; б) 2 дм; в) м; г) см.

Задание 2. Шар радиуса 4 дм пересечен плоскостью, находящейся на расстоянии 3 дм от центра. Найти площадь сечения.

№40 Тема: Объемы тел вращения.

Цель:

· Продолжить формирование навыков решения геометрических задач.

Задание 1. Алюминиевый провод диаметром 4 мм имеет массу 6,8 кг. Найдите длину провода (плотность алюминия 2,6 г/см³). .

Задание 2. Найдите объем конуса, если его образующая равна 13 см, а площадь осевого сечения равна 60 см².

Задание 3. Сколько кожи пойдет на покрышку футбольного мяча радиуса 10 см? (На швы добавить 8% площади поверхности мяча.)

Задание 4. Конический бак имеет глубину 3 м, а его верх имеет диаметр 3 м. Сколько литров жидкости он вмещает?

№41 Тема: Тела вращения.

Цель: Сформировать понимание значимости геометрии в профессиональной деятельности и в жизни человека в целом. Научится создавать тела вращения и видеть их в окружающем мире.

Задание

1. Изготовить из бумаги, дерева или другого подручного материала геометрическую фигуру: тело вращения (цилиндр или конус, шар).

№42 Тема: Математический кроссворд (4 час.)

Цель: Повторить теоретические сведения по предмету.

Задачи:

• Продолжить формирование любознательности, интереса к предмету и грамотности обучающегося
• Продолжить формирование поисковых, творческих и исследовательских умений.

Задание Составить кроссворд, зарисовав его в тетради и записав вопросы и ответы в пустые клетки.

Требования:

1. Все слова, входящие в кроссворд, должны являться существительными-терминами из тем, пройденных в течении учебного года.

2. Минимальное количество слов на оценку 5 – 20 слов, 4 – до 15, а 3 – 10 слов.

3. Определения должны быть по во возможности краткими. Следует избегать перечислений, не злоупотреблять причастными и деепричастными оборотами, не перегружать текст прилагательными. Определение кроссворда - своего рода компромисс между краткостью и содержательностью.

4. Запрещается использование однокоренных слов в вопросах и ответах.

Критерии оценивания работ:

- разнообразие терминов, понятий, имен, названий, используемых авторами;

- оригинальность названия и содержания кроссворда;

- четкость формулировки вопросов;

- дизайн кроссворда, использование оригинальных форм и элементов оформления;

- соответствие работы заявленной тематике;

- соблюдение минимального количества слов;

- достоверность информации;

№43 Тема: Сложение и умножение вектора на число.

Цель:

· Продолжить формирование навыков решения геометрических задач.

Задание 1.

Задание 2.

№44 Тема: Формула расстояния между двумя точками.

Цель:

· Продолжить формирование навыков решения геометрических задач.

Задание 1.

Задание 1.

№45 Тема: Производные элементарных функций.

Цель: Продолжить формирование навыков вычисления производных элементарных функций.

Задание 1. Вычислить производную функцию

а) f(x)=3 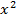б) f(x)=5 в) f(x)=
г) f(x)= д) f(x)=2 е) f(x)=

№46 Тема: Экстремумы функций.

Цель: Продолжить формирование навыков вычисления экстремумов функций.

Алгоритм нахождения экстремумов функции:

1. Находим производную ;

2. Решаем уравнение и находим и др.

3. Заполняем таблицу:

В x	(-∞;x1)	x1	(x1;x2)	x2	(x2; x3)	x3	(x2;+∞)
f(‘x)	+ или -	f’(x1)	+ или -	f’(x2)	+ или -	f'(x3)	+ или -
f(x)		f(x1)		f(x2)		f(x3)
Экстре-мумы		max или min		max или min		max или min

Задание 1. Найти экстремумы функции:

a) f(x)=2 ; b) f(x)= 3

№47 Тема: Решение задач на нахождение экстремумов.

Цель: Продолжить формирование навыков вычисления экстремумов функций.

Задание 1.

Скорость прямолинейно движущейся точки задана формулой

. Запишите формулу зависимости ее координаты х от времени t, если известно, что в начальный момент времени (t=0) точка находилась в начале координат.

Задание 2.

Точка движется прямолинейно с ускорением 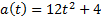. Найдите закон движения точки, если в момент t=1 с ее скорость равна 10 м/с, а координата равна 12 (единица измерения а равна ).

№48 Тема: Первообразная. Интеграл.

Цель: Продолжить формирование навыков вычисления интеграла функции.

Задание 1 Найти общий вид первообразной:

a) ;

b) ;

c) ;

d) .

Задание 2 Найти первообразную функции, если она проходит через точку М(х;у):

a) ;

b) .

№49 Тема: Площадь криволинейной трапеции.

Цель: Продолжить формирование навыков вычисления площади криволинейной трапеции.

Технология выполнения:

Пример: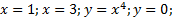

Решение:

Задание 1. Вычислить площадь криволинейной трапеции ограниченной линиями:

a)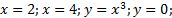

b)

c)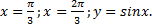

№50 Тема: Решение задач по профилю специальности (6 час.)

Цель: Сформировать навыки решения прикладных задач по профилю специальности.

Задание (для спец. «Сварщик»): Один сварщик выполняет сварочные работы по монтажу конструкции за 24 дня, другой сварщик ту же работу может выполнить за 48 дней. За сколько дней будет выполнена эта работа, если сварщики будут работать вместе?

Задание (для спец. «Автомеханик»): Колонна грузовых автомашин должна была пройти некоторое расстояние за 2,25 суток, но оказалось, что она проходила за каждый час на 2,5 км больше, чем предполагалось, а потому доехала на базу за 2 суток. Какое расстояние должна была пройти колонна?

Задание (для спец. «Повар, кондитер»): Цех поваров должен был к определенному сроку изготовить 360 тортов. Перевыполняя дневную норму на 9 тортов, цех за день до срока перевыполнил плановое задание на 5%. Сколько тортов изготовит цех к сроку, если будет продолжать работать с той же производительностью труда?

Задание (для спец. «Мастер по обработке цифровой информации»): Две фирмы приобрели компьютеры. Первая организация израсходовала на них 300 т.р., а вторая, купившая на 5 компьютеров меньше и заплатившая за каждый компьютер на 3 т.р. меньше первой организации, уплатила за компьютеры 180 т. р. Сколько компьютеров купила каждая организация?