
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Поняття про орфограму «*рфогр&фія*. У Зв'язку З ЦИМ
Дата добавления: 2015-10-19; просмотров: 1499
|
|
С помощью номинальной шкалымы измеряем такие переменные, которые в принципе не могут количественно отличаться друг от друга. Другое название этого уровня измерений — шкала наименований, что довольно точно отражает его сущность: каждое значение здесь представляет собою отдельную категорию, и зна- чение является просто своего рода ярлыком или именем. Значе-ния присваиваются переменной безотносительно к упорядочива- нию или установлению какой-то дистанции между категориями, их невозможно сравнивать между собою по принципу «больше-меньше», «выше-ниже» и т.п. Так, если бы мы захотели рассчи-' тать средние значения переменных, измеренных по номинальной шкале, то это было бы пустой тратой времени. В самом деле, мож-но ли рассчитать среднее значение пола? Или рода занятий^ В измерениях номинального уровня отсутствуют те свойства, ко-торыми обладают реальные числа, и такие переменные невозмож|-но складывать, вычитать, умножать и делить13.
Поэтому данные, полученные по номинальной шкале, обыч-но резюмируются с помощью простого частотного распределения так, как показано в табл. 4.2 и 4.3.
| Распределение респондентов по полу | Таблица 4.2 | |||
| ПОЛ | Частота | Процент | ||
| Мужчины | 44,3 | |||
| Женщины | 55,0 | |||
| Всего | 100,0 |
Источник: Аналитический отчет об опросе избирателей округа № 14 г. Нижнего Новгорода, проведенного 12—13 марта 1998 г.
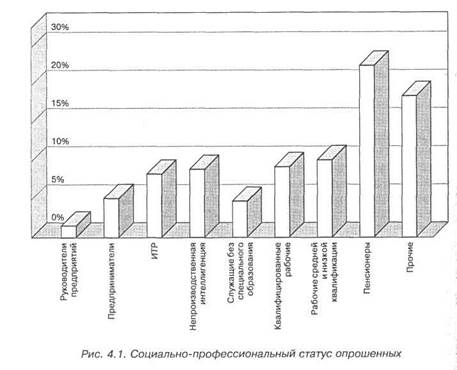
Таблица 4.3 Распределение респондентов по социально-профессиональному статусу
| Социально-профессиональный статус | Частота | Процент |
| Руководители предприятий | 1,8 | |
| Предприниматели | 5,8 | |
| ИТР | 9,3 | |
| Непроизводственная интеллигенция | 9,9 | |
| Служащие без специального образования | 5,4 | |
| Квалифицированные рабочие | 10,4 | |
| Рабочие средней и низкой квалификации | 11,4 | |
| Неработающие пенсионеры | 25,3 | |
| Прочие | 20,8 | |
| Всего | 100,0 |
Источник: Аналитический отчет об опросе 12—13 марта 1998 г.
Мы видим, что в таблицах, помимо указания частоты в абсолютных цифрах, приведены данные в процентах (что указывает на удельный вес каждого из значений определяемой переменной). Пропорции и процентные доли в процессе анализа предпочтительнее частотных распределений вследствие того, что они облегчают процесс сравнения двух популяций различных размеров. Например, в табл. 4.4 показаны две гипотетические студенческие популяции различных размеров, но с одинаковыми пропорциями выбора дисциплин, которые представляются им предпочтительными для изучения. Вы можете прикрыть полоской бумаги столбцы, содержащие проценты, и убедиться, что непосредственно из частотного распределения (без указания процентов) выявить этот факт было бы довольно трудно. Проценты же раскрывают эту информацию немедленно, поэтому нередко, в целях экономии 196
места, особенно в достаточно больших по размерам таблицах, показывают только проценты. Частотные распределения в абсолютном выражении опускаются, однако при этом желательно приводить общее число наблюдений и тем самым давать возможность читателю в случае необходимости вычислить соответствующее частотное распределение.
Таблица 4.4 Распределение предпочтений, отдаваемых различным учебным дисциплинам
| Учебная дисциплина | Экономический факультет | Коммерческий факультет | ||
| частота | процент | частота | процент | |
| Маркетинг | 25,9 | 25,9 | ||
| Социология | 22,2 | 22,2 | ||
| Английский язык | 33,3 | 33,3 | ||
| Математика | 18,5 | 18,5 | ||
| Всего | 100,0 | 100,0 |
Источник: Гипотетические данные.
В табл. 4.5 представлен пример частотного распределения, пропорций и процентов голосов делегатов Национальной конвенции Демократической партии США, поданных в 1984 г. за выдвижение трех главных кандидатов в президенты от этой партии — Уол-i, тера Мондейла, Гэри Харта и Джесси Джексона.
Таблица 4.5
Частотное распределение, пропорции и проценты голосов делегатов
Национальной демократической конвенции 1984 г.
(Переменная: число поданных голосов на номинации кандидата в президенты от Демократической партии 1984 г.)
| Категория (значение переменной) | Частота | Пропорция | Процент |
| Мондейл | 0,568 | 56,8 | |
| Харт | 0,311 | 31,1 | |
| Джексон | 0,121 | 12,1 | |
| Всего | 1,000 | 100,0 |
Источник: New York Times, July 20. 1984. A12.
Из этой таблицы, конечно, и так видно, что абсолютное числе голосов, поданных за Мондейла (2191), больше, нежели числе голосов, поданных за других кандидатов; однако, благодаря ис-
пользованию пропорций и процентов, сопоставление различных значений переменных становится более рельефным и отчетливым, что, конечно же, облегчает анализ. Преимущество становится особенно бесспорным при необходимости последовательного сравнения достаточно длинных рядов распределений.
Для данных номинального уровня измерение центральной тенденции производится с помощью определения моды. Модой, или модальной категорией, называется то значение переменной, которое встречается среди данных наиболее часто. В табл. 4.2 модальную категорию представляют собою женщины. В табл. 4.3 — это категория неработающих пенсионеров, которых среди респондентов оказалось большинство.
Помимо центральной тенденции измеряют и дисперсию данных. Дисперсия характеризует разброс значений переменной. Для данных номинального уровня наибольшая дисперсия проявляется в тех случаях, когда наблюдения распределены поровну между категориями. Данные табл. 5 весьма дисперсны, поскольку имеется почти одинаковое число мужчин и женщин. Полное отсутствие дисперсии проявляется в тех случаях, когда все наблюдаемые значения переменной совершенно однородны, т.е. попадают в одну и ту же категорию.
При проведении одномерного анализа могут обнаружиться такие характеристики данных, которые представляют собой существенные препятствия для дальнейшего анализа. Представьте, например, что вы намереваетесь изучить взаимосвязь между полом и родом занятий и обнаружили, что в выборке опроса оказались одни лишь мужчины, Поскольку налицо отсутствие дисперсии (т.е. нет вариаций по одной из ключевых переменных — по полу), сравнение провести нельзя. Урок, который необходимо из этого усвоить, состоит в следующем: нет изменения — нет сравнения.А процедура сравнения являет собою, по сути, ядро анализа. При отсутствии изменений вы можете обнаружить какое-то интересное единообразие, но не сможете изучить связей между переменными, т.е. выявить, что же происходит с одной из них, когда другая варьирует (изменяется). Самый простой одномерный анализ, проведенный в ходе сбора данных, поможет вам вовремя скорректировать выборку.
Выявляя центральную тенденцию, следует сразу обращать внимание на максимальные и минимальные значения изучаемой переменной. Другими словами, когда вы имеете дело с переменной, принимающей целый ряд значений, анализ следует начинать с акцента на самом большом и самом маленьком значении — это сразу дает вам представление о масштабах изменения рассматриваемой переменной.
198
Не менее, а нередко и более удобным средством анализа служит графическое отображение рядов распределений. На рис. 4.1 в виде столбчатой диаграммы14 изображено распределение, представленное в табл. 4.3. Одного общего взгляда на эту диаграмму достаточно, чтобы оценить соотношение численности представителей различных социально-профессиональных групп в выборочном массиве; при взгляде на таблицу это нельзя увидеть столь отчетливо.
На рис. 4.2 мы видим другую форму графического представления данных. Здесь приведена круговая диаграмма15 реестра голосов, поданных на выдвижении кандидатов в президенты демократами в 1984 г. (табл. 4.5).

4.2.2. Ранговая шкала
В принципе та же одномерная статистика, что используется для суммирования данных номинального уровня, может быть применена и для данных рангового уровня. Данные рангового уровня измерений включают в себя категории наблюдения, которые размещены по порядку16 (от большего значения какого-то признака к меньшему его значению или, наоборот, — от меньшего к большему). Здесь методы описательной статистики более информативны, нежели методы, используемые для измерений номинального уровня. Для измерений порядкового уровня центральную тенденцию частотного распределения можно оценить с помощью как моды, так и медианы. Тогда как для измерений порядкового уровня разброс можно выявить с помощью не только дисперсии, но и среднеквадратического отклонения. Для измерений номинального уровня разброс частотного распределения можно только «ощутить», просматривая все категории. Медиана — это категория, к которой принадлежит серединное наблюдение.
Можно посмотреть, как определяется медиана на примере распределений ответов на вопрос о том, какова частота использования различных источников информации о работе городской администрации (табл. 4.6).
Здесь значения переменных — частоты использования того или иного источника — соотнесены с ранговой шкалой, значения которой меняются от категории «часто» (которой присвоен ранг 4) до «не дали ответа» (ранг 0). Учитывая, что общее число опрошенных (или число наблюдений) равно 426, половина наблюдений составит 213. Это означает, что медиана для такого источника информации, как «встречи с мэром и работниками администрации»17, 200
приходится на категорию с рангом 1 (никогда); для четырех последующих переменных — на категорию с рангом 2 (иногда); для последней переменной — «телевидение» — медиана приходится на категорию 3 (регулярно).
Таблица 4.6 Источники информации о работе городской администрации
| Источники информации | Частота/ранг | ||||
| часто | регулярно | иногда | никогда | не дали ответа | |
| Встречи с мэром и работниками администрации | |||||
| Газеты | |||||
| Общение с коллегами по работе | |||||
| Общение с родными, соседями, друзьями | |||||
| Радио | |||||
| Телевидение |
Источник: Аналитический отчет об опросе жителей г. Нижнего Новгорода, декабрь 1998 г.
Отметим, что при использовании для измерений порядкового уровня методы описательной статистики более информативны, нежели для измерений номинального уровня. В первом случае центральную тенденцию частотного распределения можно оценить как с помощью моды, так и с помощью медианы, а во втором подходит только мода. Для измерений порядкового уровня разброс частотного распределения можно выявить с помощью дисперсии и среднеквадратического отклонения, тогда как для измерений номинального уровня разброс можно только «ощутить», просматривая все категории. Такова одна из причин, по которым измерения высокого уровня часто оказываются предпочтительнее по сравнению с измерениями более низкого уровня.
4.2.3. Интервальная шкала
Измерения интервального и пропорционального уровня редко анализируются с помощью прямого указания частот или процентных отношений. В отличие от номинальных или ранговых измерений значения переменных, измеряемых с помощью интерваль-
ных шкал, изменяются непрерывно, они представляют собой численные величины, а не категории. Поэтому количество различных наблюдаемых значений может быть так велико, что частоты и процентные отношения не в состоянии эффективно просуммировать данные. В самом деле, при измерении такой переменной, как возраст, мы можем получить набор значений, ни одно из которых не будет повторять другого (если в нашем выборочном массиве не окажется какого-то количества респондентов, чьи даты рождения совпадают день в день). При измерении доходов также трудно рассчитывать, что суммы доходов различных респондентов или их семей будут совпадать до рублей и копеек. По этой причине значения таких переменных и размещают в интервалах, размеры которых определяются исследовательским замыслом.
Критериями центральной тенденции для пропорционального и интервального уровней измерений выступают мода, медиана и среднее арифметическое. Среднее арифметическое представляет собой сумму значений переменной, разделенную на число значений. Общая формула для ее вычисления алгебраически выглядит следующим образом
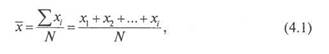
где X/— числовое значение /-й позиции, a N— общее число наблюдений (объем выборки).
Рассмотрим вычисление средней арифметической величины на примере расчета средней посещаемости занятий в студенческой группе по данным проверок деканата. Данные о посещаемости приведены в табл. 4.7.
Сложив числа в правой колонке и разделив их на 10 (число проверок), мы получим, что средняя посещаемость в группе составила х = 18,6.
Понятно, что полученное число — 18,6 студента — не может иметь реального физического смысла, оно пригодно лишь для сравнения между собою уровня посещаемости в двух и более группах. Хотя и для этой цели полученные средние величины вначале следует нормировать, разделив их на общую численность студентов каждой группы.
Среднее может оказаться обманчивым показателем центральной тенденции, если в объеме выборочной совокупности среди значений интересующей нас переменной появится какая-то экстремальная величина. Например, среднедушевые ежемесячные доходы семей в двух гипотетических общинах (скажем, среди жильцов двух подъездов одного дома, каждый из которых насчитывает по 10 квар-
тир) идентичны, за исключением дохода одной семьи (табл. 4.8). Среднедушевой доход семьи жителей 1 -го подъезда — 4230 руб. — более чем вдвое превышает среднедушевой доход во 2-м подъезде — 2050 руб. Именно расчет среднего дохода в каждом из подъездов создает ошибочное впечатление, что люди в 1 -м подъезде вдвое богаче, чем люди во 2-м подъезде, тогда как в реальности есть лишь одна семья в 1-м подъезде, которая гораздо богаче любой семьи из обоих подъездов. В этом случае медиана будет лучшим показателем центральной тенденции, нежели среднее. Медианный подход даст для обоих подъездов одинаковый результат: 2100 руб. — довольно близкий к среднему значению по 2-му подъезду. Если среднее и медиана не сходны по своему значению, можно сделать вывод, что на значение среднего влияют одно или несколько экстремальных значений измеряемой переменной.
Таблица 4.7 Посещаемость занятий студентами академической группы
| Номер занятия | Число присутствующих | |
| Номер занятия | Число присутствующих | |
Источник: Гипотетические данные.
Таблица 4.8 Среднедушевые ежемесячные доходы семей в двух подъездах дома (руб.)
| Номер квартиры | 1-й подъезд | Номер квартиры | 2-й подъезд |
| 25 000 | |||
| Среднее | Среднее |
Вычисление средней арифметической величины для переменных, значения которых измеряются не однозначно определенными числами, а изменяются вдоль непрерывного ряда значений, имеет свои особенности. Здесь расчитывается не среднее арифметическое, а средневзвешенное. Предположим, что нам требуется вычислить средний возраст опрошенных респондентов (табл. 4.9).
Таблица 4.9
Распределение респондентов по возрасту
| Возраст, годы | Частота | Процент |
| 18-24 | 10,1 | |
| 25-29 | 12,0 | |
| 30-39 | 21,2 | |
| 40-49 | 25,2 | |
| 50-59 | 16,2 | |
| 60-70 | 15,3 | |
| Всего | 100,0 |
Источник: Аналитический отчет об опросе жителей г. Нижнего Новгорода, декабрь 1998 г.
Вначале мы должны определить середину каждого интервала; это делается путем вычисления простого среднего, т.е. сумма крайних значений делится пополам. Затем необходимо умножить это значение на число респондентов соответствующего возраста, сложить полученные произведения и разделить на общий объем выборки (см. табл. 4.9а).
Таблица 4.9а Результат 2-го этапа вычисления средневозрастной величины
| Возраст, годы | Частота | Середина интервала | Произведение |
| 18-24 | |||
| 25-29 | |||
| 30-39 | 34,5 | 3346,5 | |
| 40-49 | 44,5 | 5117,5 | |
| 50-59 | 54,5 | ||
| 60-70 | |||
| Всего | I | 19 498 |
Источник: Гипотетические данные.
Разделив полученную сумму на 457, мы получим средний возраст в 42,6 года. Таким образом, формула для средневзвешенного значения выглядит аналогично соотношению (4.1) с учетом того, что X/ здесь относится к середине интервала:
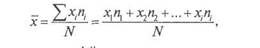
где Xj — числовое значение /-й позиции; п{ — число респондентов, наблюдаемых по /-и позиции переменной; N— общее число наблюдений.
Показатели разброса данных интервального или пропорционального уровня включают среднее отклонение, дисперсию и сред-неквадратическое отклонение. Среднее отклонение (MD) представляет собой меру разброса, основанную на отклонении каждого из значений от среднего. Пример ее вычисления приведен ниже, по данным из табл. 4.10.
Таблица 4.10
Распределение, отклонение и среднее распределение доходов среди жильцов подъезда № 2
| Номер квартиры | 2-й подъезд | х-х | \х-х\ |
| -1050 | |||
| -1050 | |||
| -850 | |||
| -150 | |||
| -50 | |||
| Среднее | S(x-x)=0 |
Таким образом, уравнение для среднего отклонения выглядит следующим образом:

где | | — символ абсолютной величины (модуля).
Если мы берем каждую отметку и вычитаем из нее среднее, мы вычисляем ту величину, на которую каждая из отметок (вторая колонка) отличается от среднего (нижняя ячейка второй колонки). Сумма этих отклонений всегда равна нулю — важное математическое свойство среднего (проверьте это сами, сложив числа в третьей колонке). Поскольку мы интересуемся только величиной отклонения, а не направлением или знаком его, то находим абсолютные значения отклонения (четвертая колонка). Затем мы 205
берем их сумму и делим на число отметок, чтобы найти среднее отклонение отметок от среднего; получаем MD = 630. Чем больше среднее отклонение, тем сильнее разброс отметок вокруг среднего.
Хотя среднее отклонение и выявляет разброс, чаще для его измерения используются дисперсия и среднеквадратическое отклонение.

Дисперсия представляет собой сумму квадратов отклонений от среднего, разделенную на число отметок:

Среднеквадратичвское отклонение представляет собою корень квадратный из дисперсии:
Чем больше разброс данных вокруг среднего, тем выше значения ст2 и S. Это означает, что если все данные одинаковы, то s2 и Нравны нулю.
Таким образом, для вычисления дисперсии и среднеквадрати-ческого отклонения надо пройти последовательно семь этапов:
1) вычислить среднее;
2) вычислить разности между средним и каждым из значений;
3) возвести в квадрат разности, вычисленные на этапе 2;
4) умножить квадраты разностей на частоты наблюдений каждого из значений;
5) просуммировать квадраты разностей, вычисленные на этапе 4;
6) разделить сумму квадратов, полученную на этапе 5, на N; это равняется дисперсии;
7) извлечь квадратный корень из числа, вычисленного на этапе 6; это равняется среднеквадратическому отклонению.
Пример расчета дисперсии и среднеквадратического отклонения. В опросе, проведенном в конце декабря 1998 г., нижегородцев просили оценить некоторые личностные качества недавно избранного мэра, используя для этого так называемый семантический дифференциал18. Этот метод заключается в следующем:
респонденту предлагается выразить свое отношение к интересующему исследователя качеству по совокупности биполярных шкал (в нашем случае девятибалльных). Одно из предложенных для оценки качеств мэра — доступность — было выражено с помощью такой шкалы:
| доступный | 9|8 | неприступный |
Результаты в исследовании распределились следующим образом:
Таблица 4.11
Распределение оценок качества «доступность»
| Оценочный балл | Частота |
| Нет ответа | |
| Всего |
Отбросив нули (табл. 4.11), т.е. варианты «нет ответа» (после чего Остановится равным 368), мы подсчитываем, что среднее значение оценки (по формуле средневзвешенного) составляет:
х = 5,42.
Обратим внимание: если бы мы не отбросили значение «нет ответа», т.е. приняли бы эту позицию за нуль как математическую величину, то получили бы среднее значение:
х = 4,67,
т.е. заметно меньшее, нежели рассчитанное нами. Оно более точно в математическом смысле, но искажает социологический смысл, поскольку ведь те, кто не дали ответа, вовсе не выставляли оценку «0», они просто не выставили никакой оценки.
Рассчитаем отклонение от среднего и квадрат отклонения от среднего по каждому баллу (табл. 4.12).
| Образец расчета | Таблица 4.12 | |
| х, (оценочный балл) | (х,-х) | (х,-х)' |
| -4,4 | 135,52 | |
| -3,4 | 127,16 | |
| -2,4 | 230,4 | |
| -1,4 | 90,16 | |
| -0,4 | 17,28 | |
| 0,6 | 18,36 | |
| 1,6 | 140,8 | |
| 2,6 | 162,24 | |
| 3,6 | 336,96 |
Сложив числа крайней правой колонки, мы получим:

дисперсия:

среднеквадратическое отклонение:

Что дает для анализа данных знание дисперсии? Напомним, что «дисперсия» (dispersion) по-английски означает «разбрасывание, рассеивание»; в данном случае это рассеяние реально полученных эмпирических данных вокруг среднего значения. В зависимости от того, насколько велика (точнее, мала) дисперсия или среднеквадратичное отклонение, мы можем судить, насколько единодушны были в своих оценках респонденты (при меньшем значении дисперсии), или наоборот — насколько сильно они расходятся в своих мнениях (при большем значении дисперсии)19. Сравним, к примеру, разброс оценок (по пятибалльной шкале: от 5 — очень важное, до 1 — затрудняюсь ответить), которую, в ходе исследования особенностей сексуального поведения, дали респонденты степени влияния на их «сексуальное образование» различных источников информации (табл. 4.13):
Таблица 4.13
Оценка степени влияния различных источников на информированность о сфере интимных отношений (в средних значениях по 5-балльной шкале)
| Источник | Среднее | S |
| Сексуальный партнер | 3,55 | 1,36 |
| Супруг(а) | 3,12 | 1,58 |
| Друзья | 3,07 | 1,14 |
| Эротические фильмы | 3,02 | 1,09 |
| Популярные издания | 2,93 | 1,20 |
| Научная литература | 2,81 | 1,15 |
| Эротическая литература | 2,81 | 1,14 |
| Родители | 2,36 | 0,92 |
| Педагоги | 2,13 | 0,82 |
| Другие источники | 2,38 | 1,25 |
Источник: Данные пилотажного опроса, декабрь 1998 г.
Из этой таблицы помимо сведений о том, что максимальное влияние на информированность о наиболее интимных сторонах жизни оказывает сексуальный партнер, а наименьшее — педагоги, мы узнаем также, что с наибольшим единодушием респонденты оценили низкую степень влияния такого источника, как педагоги, о чем говорит минимальное значение среднеквадратического отклонения, а наибольшее расхождение в оценках вызвал такой источник, как супруг/супруга, — максимальное значение S (что, возможно, связано с большими различиями в индивидуальном опыте).
4.3. Анализ двумерных распределений
Одной из важных задач любого анализа данных является проверка гипотез, сформулированных в программе исследования. В гипотезе, как правило, высказывается предположение о наличии связи между двумя и более переменными. И на определенном этапе анализа следует заняться поиском таких связей. Чтобы проделать это, в идеале необходимо найти ответ на пять основных вопросов:
1. Существует ли обозначенная в гипотезе связь между независимой и зависимой переменными?
2. Каково направление этой связи?
3. Насколько сильна связь?
4. Является ли связь статистически значимой?
5. Является ли связь каузальной?
Начнем с поисков ответа на первый вопрос. Мы можем утверждать, что связь существует, если наблюдаемые значения незави-
симой переменной ассоциируются с наблюдаемыми значениями зависимой переменной. Предположим, мы сформулировали гипотезу: «чем старше избиратели, тем больше вероятность того, что они примут участие в выборах». При анкетировании мы задаем прямой вопрос с предлагаемыми вариантами ответов:
| <== предыдущая лекция | | | следующая лекция ==> |
| І позначення ^ * ? гігііігі | | | ОРФОГРАФІЧНІ ВПРАВИ |