Ціль викладання дисципліни

Дата добавления: 2015-03-11; просмотров: 640

Рассмотрим теперь II зону (припотолочный слой нагретых газов). Объем этой зоны в момент времени τ равен

где F_П0T - площадь потолка; у_к - координата нижнего края припотолочного слоя газов. Масса газа, заключенная во II зоне, составляет величину т₂ = р₂V₂ Давление в зоне II практически не меняется и остается равным начальному значению, т.е. Р₀. Внутренняя (тепловая) энергия II зоны составляет:

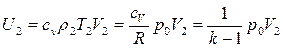
Запишем уравнения материального баланса и энергии для II зоны применительно к первой фазе начальной стадии пожара:

(6.4)

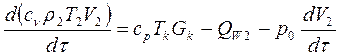(6.5)

где ρ₂ - средняя плотность во II зоне; Т₂ - средняя температура во II зоне; Q_w2 - тепловой поток от припотолочного слоя газа в ограждения, кВт.

Параметры состояния Т₂ и ρ₂ связаны между собой следующим уравнением:

(6.6)

Уравнение (6.6) следует из условия равенства давлений во всех зонах. Это условие является приближенным, но применимым для реальных пожаров.

Преобразуем уравнение энергии (6.5), используя уравнение (6.6):

или

и окончательно 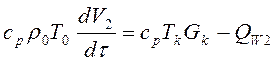(6.7)

Из уравнения (6.1) следует:

Подставляя формулу (6.8) в уравнение (6.7), получим:

Примем, что (для начальной стадии φ= 0,66).

После дальнейших преобразований получим следующее уравнение:

(6.8а)

Подставим в это уравнение выражение для G_k (6.2):

(6.9)

Отметим, что в этом уравнении

Введем обозначения:

Функции β(τ) и γ(τ) при горении твердых ГМ в момент времени τ = 0 равны нулю, так как F_Г → 0. Уравнение (6.9) принимает вид:

(6.10)

Начальное условие .

Решение уравнения (6.10) при заданном начальном условии будем искать для интервала времени от τ = 0 до τ_*, где τ_* - момент окончания первой фазы начальной стадии пожара. После того как найдена функция у_к(τ), находим G_k =f₁(τ); V₂ =f₂(τ).

Преобразуем уравнение материального баланса (6.4). Интегрируя его, получаем:

(6.11)

После преобразований из формулы (6.11) получаем:

(6.12)

После вычислений плотности ρ₂ определяется средняя температура в припотолочном слое газа:

(6.13)

Уравнение баланса для токсичного газа (продукт горения) во II зоне имеет вид:

(6.14)

где ρ_n - парциальная плотность токсичного газа; L - количество (масса) токсичного газа, образующаяся при сгорании 1 кг горючего материала. Из формулы (6.14) следует формула:

(6.15)

где М_τ - количество (масса) ГМ, выгоревшего к моменту времени τ.

Уравнение дыма для припотолочного слоя имеет вид:

и, следовательно:

Исходя из выше изложенного, имеем уравнение с разделяющимися переменными, с помощью которого рассчитывается изменение координаты границы припотолочного слоя в течение времени:

где:

при условии: y₀ =const;

Выводы по лекции: зонная модель представляет собой опять же частный случай интегральной модели для припотолочного слоя, и с применением известных теорий, в частности - теории конвективной колонки.

ЛЕКЦИЯ

по дисциплине "Прогнозирование опасных факторов пожара"

Тема №7 «ДИФФЕРЕНЦИАЛЬНЫЕ (ПОЛЕВЫЕ) МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОЖАРА В ПОМЕЩЕНИИ. ЧИСЛЕННАЯ РЕАЛИЗАЦИИ ПОЛЕВОЙ МОДЕЛИ»

План лекции:

Введение

1 Развитие полевого моделирования пожара в помещении

2 Модель очага горения

3 Модель начальной стадии пожара в декартовых координатах

4 Модель начальной стадии пожара в цилиндрических координатах.

5 Алгоритм реализации модели.

Выводы

Цели лекции:

1.Учебные

В результате прослушивания материала слушатели должны знать:

- опасные факторы пожара, воздействующие на людей, на конструкции и оборудование

- предельно допустимые значения ОФП

- методы прогнозирования ОФП

Уметь: прогнозировать обстановку на пожаре.

2.Развивающие:

- выделять самое главное

- самостоятельность и гибкости мышления

- развитие познавательного мышления

Литература

1. Федеральный закон № 123-ФЗ. от 22 июля 2008 г. Технический регламент о требованиях пожарной безопасности.

2. Моделирование пожаров и взрывов. (Под ред. Брушлинского Н.Н. и Корольченко А.Я.) - М.: Пожнаука, 2000, - 492 с.

Введение

Наиболее детальный уровень моделирования могут обеспечить, в принципе, полевые модели пожара. Эти модели называют дифференциальными. Полевые модели базируются на использовании дифференциальных уравнений в частных производных, описывающих пространственно-временное распределение температур и скоростей газовой среды в помещении, концентраций компонентов газовой среды (кислорода, продуктов горения и т.д.), давлений и плотностей. Эти уравнения включают реологический закон Стокса, закон теплопроводности Фурье, законы диффузии, законы радиационного переноса и т.п. Система уравнений, описывающих изменения во времени указанных параметров газовой среды в каждой точке пространства внутри помещения чрезвычайно громоздка. Решение названной системы осуществляется с помощью мощных ЭВМ. Результаты решения получаются в форме полей скоростей, температур, концентраций продуктов горения и кислорода в любой момент времени протекания пожара.