
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Поняття та склад зобов'язання
Дата добавления: 2015-03-11; просмотров: 652
|
|
В аналізі й прогнозуванні економічної кон'юнктури широко використовуються методи фінансових розрахунків. Показники, які розраховують на основі цих методів, є за своєю сутністю індикаторами кон'юнктури. Є й зворотна залежність фінансових обчислень від кон'юнктури – її зміна впливає, як правило, на базу фінансових розрахунків.
Приклад: щомісячний ріст інфляції призводить до збільшення щорічної банківської процентної ставки.
Оцінка динаміки кон'юнктури простих і складних процентів по ряду господарських і фінансових операцій необхідна для прогнозування ситуації на ринку. Крім того, застосування перерахованих фінансових інструментів необхідне для розрахунку самих індикаторів кон'юнктури (визначення валютних курсів, обсягів продажу і т.д.). Без знання сутності фінансових обчислень неможливо оцінити зміну кон'юнктури того або іншого фінансового показника (індикатора).
Прості та складні проценти.
Найважливішим елементом фінансових розрахунків є дохід, одержуваний від виконаної угоди – так званий процент або процентний дохід. Це може бути дохід від надання кредиту, проведення брокерської операції з товаром або цінними паперами і т.д.
При укладанні угоди сторони домовляються про розмір процентів, встановлюваних відношенням доходу від проведення угоди до загальної суми угоди, виплачуваної за одиницю часу. Отриману величину називають декурсивною ставкою процента. Виражається вона у вигляді десяткового або натурального дробу.
Нарахування процентів відбувається залежно від умов угоди, встановлюваних періодом нарахування – раз на рік, півріччя, квартал, місяць.
Дохід по процентах від укладеної угоди розраховується за формулою (слайд 17):
І=і∙Р∙п,
де І – дохід по процентах;
і – ставка процента;
Р – первісний обсяг угоди (боргу);
п – число періодів нарахувань.
Збільшення суми грошей по ходу сплати процентів називають нарощуванням або ростом первісної суми.
На практиці нерідко процентна ставка змінюється залежно від періоду її застосування, у цьому випадку сума боргу розраховується за формулою (слайд 18):
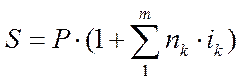 ,
,
де ik – ставка простих процентів для періоду k =l..m;
пk – тривалість періоду k.
Приклад (слайд 19): фірма одержала позичку під капітальні вкладення в розмірі 7 тис. грошових од. під 4% річних на термін 4 роки. У цьому випадку сума, яку необхідно сплатити до моменту закінчення чотирьох років, повинна становити S = 7 000 (1+4x0,04) = 8 120 гр. од.
Після закінчення чотирьох років термін погашення був перенесений ще на два роки з умовою виплати 10% річних. Загальна сума боргу повинна вже досягти S = 7 000 (1+4x0,04+2x0,10) = 9 520 гр. од.
Ставки процентів по кредитах банків варіюють залежно від особливостей позичальника. Великі банки відносно надійних позичальників визначають кращі ставки, які виступають індикаторами відносно інших позичальників. Такі ставки називають "прайм рейт" (prime rate). При встановленні "прайм рейт" враховується загальногосподарська кон'юнктура, наявність грошових резервів і динаміка кон'юнктури процентних ставок.
Часто укладаються угоди, у яких обумовлюється вилучення суми процентів з надаваної позички. За заданою сумою, яку потрібно сплатити через обумовлений у договорі термін, визначається розмір позички при обговореному позичковому проценті. У такому випадку вважається, що розмір позички дисконтується. Різниця між сумою боргу і розміром позички називається дисконтом. У дисконтних розрахунках використовують дисконтування, при якому за сумою боргу (сумі оплати угоди), позичковій ставці (ставці доходу) потрібно визначити первісний розмір позички (обсяг угоди) (слайд 20):
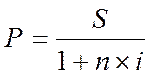 ,
,
де Р – розмір позички (обсяг угоди);
S – сума боргу (сума оплати угоди);
i – позичкова ставка (ставка доходу по угоді);
n – число періодів нарахування процентів по угоді.
Приклад (слайд 21). 100 000 гр. од. слід сплатити через 4 місяці з розрахунку простих щомісячних 5%, при цьому дохід кредитора з позички вилучається. У цьому випадку сума позички повинна становити: Р = 100 000 гр. од./ (1+4x0,05) = 83 333 гр. од.
В практиці довгострокових розрахунків відбувається капіталізація процентів за угодою. Їхня сума додається до первісної вартості капіталу і на наступному етапі розрахунків отриманий підсумок приймається за розрахункову величину. У такий спосіб процес нарощування первісної суми йде з більшим прискоренням, ніж при нарахуванні простих процентів (слайд 22).
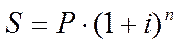
Приклад. Позика в 1000 гр. од. видана на три роки зі ставкою 17% річних. Нарощена сума на момент погашення становитиме S = 1000 гр.од. (1+0,17)3 = 1000x1,6016 = 1601,6 гр.од.
Аналогічно дисконтуванню по простих процентах розраховується дисконт по складних процентах (слайд 23):
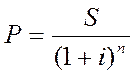 ,
,
Приклад: потрібно визначити сучасну величину платежу для нарощеної суми в 1200 гр.од., яка буде отримана через три роки при річній процентній ставці 10%:
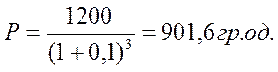
У фінансових угодах при урахуванні фактору інфляції суму нарощування коректують на величину, обернену до індексу інфляції (якщо потрібно визначити реальну нарощену суму в діючих цінах) (слайд 24):
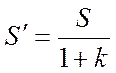 ,
,
де S – “реальна” нарощена сума з урахуванням інфляції;
k – темп інфляції.
Таким чином, формула, яка відображає приріст капіталу на основі складних процентів з урахуванням темпів інфляції буде мати наступний вигляд:
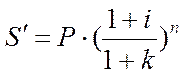
Отримана величина відображає майбутню нарощену суму в діючих цінах.
Приклад (слайд 25): Потрібно розрахувати реальну нарощену протягом п’яти років суму боргу з урахуванням інфляції при процентній ставці 20% річних і передбачуваного рівня інфляції, рівного 21% річних. Розмір кредиту – 10000 гр.од. В даному випадку нарощена сума боргу дорівнюватиме:
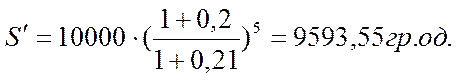
Тобто реально нарощена сума з урахуванням інфляції менша первісного боргу.
Аналіз даної формули з точки зору урахування впливу зміни кон’юнктури процентних ставок і динаміки інфляції дозволяє зробити такі висновки:
1) якщо i = k, то нарощування дорівнює нулеві;
2) якщо i > k, то первісна сума зростає на коефіцієнт перевищення, рівний w=(1+i)/(1+k);
3) якщо i < k, то первісна сума зменшиться на коефіцієнт w=(1+i)/(1+k).
Таке кон’юнктурне поєднання називають “ерозією” капіталу.
Фінансові ренти (слайд 26)
У господарських операціях і фінансових угодах передбачаються не окремі виплати, а дискретний потік платежів. Послідовність платежів, які настають через рівні проміжки часу, називають фінансовою рентою, незалежно від походження платежів, їхнього призначення і цілей. Окремий платіж називають ануїтетом.
Наприклад, фінансовою рентою є платежі по погашенню споживчого кредиту.
Величину кожного окремого платежу називають членом ренти. Період ренти – це інтервал між платежами. Час від початку настання рентних стосунків до кінця останнього періоду виплати називається строком ренти. Процентна ставка – ставка, використовувана при розрахунку нарощування або дисконтування платежів по ренті.
При проведенні фінансово-економічних розрахунків використовуються різні види ренти.
Залежно від частоти виплат ренти діляться на річні, р-строкові (р – число виплат протягом року) і безперервні (виплати проводяться дуже часто) (слайд 27).
Залежно від розмірів платежів ренти діляться на постійні та змінні (у різні періоди платежів розміри платежів різні).
Ренти, які підлягають обов'язковій сплаті, називають обов'язковими. Якщо виплата ренти залежить від настання якої-небудь події або умови, така рента називається умовною.
Залежно від числа періодів платежів ренти діляться на обмежені і вічні ренти.
По настанню першого строку платежу ренти діляться на негайні та відстрочені.
За моментом виплати ренти діляться на постнумерандо (строк платежу настає наприкінці періоду) і пренумерандо (платіж здійснюється на початку періоду ренти).
Нарощена сума ренти – це сума всіх членів ренти з нарахуванням на них процентів до кінця строку ренти.
Для постійної річної ренти нарощена сума розраховується за формулою (слайд 28):
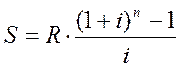 ,
,
де S – нарощена сума ренти;
R – розмір платежу (члена) ренти;
i – ставка процентів по ренті;
n – строк ренти.
Введение в специальность
| <== предыдущая лекция | | | следующая лекция ==> |
| Навчальний матеріал. Пункт 1. | | | Елементи зобов'язань |