Случайные величины и их вероятностные характеристикиЕсли случайная величина ξ может принимать конечное число дискретных значений xi, исчерпывающей вероятностной характеристикой ее служит распределение вероятностей этих значений Pi. (По аналогии со случайными функциями случайные величины обозначим буквами греческого алфавита, а их конкретные реализации – буквами латинского алфавита.) Если случайная величина ξ непрерывна и может принимать любое значение на интервале [xmin, xmax], то ее статистической характеристикой может служить так называемый интегральный закон распределения F (x)=P(ξ < x), определяющий вероятность того, что случайная величина ξ не превзойдет значение x. Из определения интегрального закона распределения вытекает следующее очевидное соотношение:
где Очевидны следующие свойства функции F(x): F(x) – монотонная неубывающая функция;
Если функция F(x) дифференцируемая, то в качестве вероятностной характеристики случайной величины удобно использовать дифференциальный закон распределения или закон распределения плотности вероятности
Очевидны следующие соотношения:
Помимо законов распределения, часто используются числовые характеристики случайных величин, так называемые моменты распределения. Моменты, характеризующие распределение случайных величин относительно нуля, называются начальными. Для непрерывных случайных величин начальный момент k-го порядка определяется по формуле
Для дискретной случайной величины ξ;, принимающей значения x1, x2, …, xn с вероятностями P1, P2, …, Pn,
Наиболее важное значение имеют моменты 1-го и 2-го порядков. Начальный момент 1-го порядка дает математическое ожидание или среднее значение случайной величины ξ;:
Разность Δ ξ =ξ – m1(ξ) называется отклонением случайной величины. Моменты распределения отклонений случайной величины называются центральными и обозначаются Mk(ξ). Нетрудно убедиться, что M1(ξ)=0. Случайные величины с нулевым средним значением называются центрированными. Любые случайные величины можно свести к центрированным, если перейти к отклонениям Δ ξ . Начальный момент 2-го порядка определяет средний квадрат случайной величины ξ;:
Центральный момент 2-го порядка называется дисперсией случайной величины:
Отношение Δ ξ /σ ξ называется нормированным отклонением случайной величины. Центральный и начальный момент 2-го порядка случайной величины связаны простым соотношением:
Для совокупности двух случайных величин ξ 1 и ξ 2 исчерпывающей вероятностной характеристикой служит двумерный интегральный закон распределения F(x1, x2)=P(ξ 1< x1, ξ 2< x2), определяющий вероятность того, что случайные величины ξ 1 и ξ 2 не превосходят соответственно значений x1 и x2. Если функция F(x1, x2) дифференцируемая, то вероятностной характеристикой двумерной случайной величины может служить двумерный дифференциальный закон распределения или двумерная плотность вероятностей ω 2(x1, x2)=∂ 2F(x1, x2)/∂ x1∂ x2. Аналогично могут быть введены многомерный интегральный закон распределения и многомерные функции распределения для совокупностей из любого числа случайных величин. Можно также ввести числовые характеристики для совокупности двух случайных величин ξ 1 и ξ 2, имеющих двумерную плотность вероятностей ω 2(x1, x2). Весьма важной числовой характеристикой совокупности двух случайных величин является смешанный второй центральный момент или ковариация случайных величин ξ 1 и ξ 2:
Если случайные величины ξ 1 и ξ 2 независимы, то ω 2(x1, x2)=ω (x1)ω (x2), и двукратный интеграл в (2.22) распадается на произведения двух однократных интегралов:
и, следовательно, M2(ξ 1, ξ 2)=0. Поэтому ковариация M2(ξ 1, ξ 2) может служить некоторой мерой зависимости между двумя случайными величинами. Чаще в качестве такой меры принимают безразмерный коэффициент корреляции
Две случайные величины, для которых коэффициент корреляции равен нулю, называются некоррелированными. Случайные величины, для которых 1-й начальный момент их произведения
называют ортогональными. Если средние значения случайных величин равно нулю, то понятия ортогональности и некоррелированности случайных величин совпадают. Моменты распределения того или иного порядка, являясь важными числовыми характеристиками случайной величины, не являются, однако, их однозначной полной статистической характеристикой: случайные величины, имеющие одинаковые 1-й и 2-й моменты, могут иметь разные законы распределения.
|


 – вероятность того, что случайная величина ξ не выйдет за пределы интервала [x1, x2].
– вероятность того, что случайная величина ξ не выйдет за пределы интервала [x1, x2].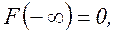

 (2.15)
(2.15)
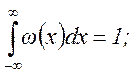

 (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20) (2.21)
(2.21)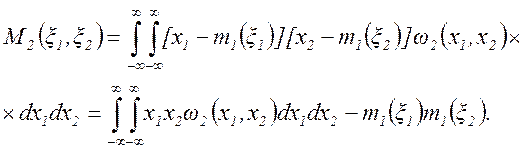 (2.22)
(2.22)






