КОЛОМЕНСКИЙ ИНСТИТУТ (ФИЛИАЛ). 2.1. Парная линейная регрессия показывает зависимость в виде Y=α +β X2.1. Парная линейная регрессия показывает зависимость в виде Y=α +β X. Электронные таблицы Excel позволяет находить уравнение парной линейной регрессии путем: - подсчета показателей по соответствующим эмпирическим формулам; - вставки тренда на график функции; - - используя стандартную функцию ЛИНЕЙН; - нахождения оценок параметров, используя операции над матрицами;
2.2. Подготовка данных для расчета. 1. Из всей системы показателей, представленной на листе «ИД» рабочей книги на листе «Начало» выбираются зависимая переменная Y и факторные переменные Х1, Х2, Х3 согласно номерам, получаемым при нажатии кнопок НАЧАЛО и ВАРИАНТ. Ввод численных значений показателей следует осуществлять не копированием, а ссылкой на лист «ИД»: в левую верхнюю ячейку (С4 листа «Начало») вводится, например, «= ИД.В7», а затем формула «растягивается» на весь диапазон. 2. Выбор одной из факторных переменных производится на основе корреляционного анализа на листе «Начало» в подготовленной области J5:M5. Коэффициенты парной корреляции находятся с помощью статистической функции «КОРРЕЛ», аргументами которой служат два множества данных. В ячейку J5 вводим, например, «=КОРРЕЛ(C4:C65;C4:C65)». Адреса ячеек первого множества следует сделать абсолютными: «=КОРРЕЛ($C$4:$C$65;C4:C65)», это позволит распространить введенную формулу на всю строку занчений парных коэффициентов корреляции: активизируйте ячейку J5, поставьте курсор мышки на маркер заполнения, нажмите левую кнопку мышки и перетащите курсор заполнения через заполняемые ячейки, отпустите левую кнопку мышки. 3. Значение коэффициента корреляции показывает степень линейной связи между переменными. Для проведения парного регрессионного анализа из переменных Х1, Х2, Х3 выбираем ту, для которой абсолютная величина парного коэффициента корреляции с Y максимальна. 4. На основе расчетов, проведенных на листе Начало, делается вывод о том, какая из рассмотренных факторных переменных оказывает наибольшее воздействие на переменную Y: в ячейку М14 слдует записать «Х1», «Х2» или «Х3». При этом нужно указать в ячейках J8:J11 конкретное экономическое содержание всех включенных в модель переменных и их размерности. 5. Выбранные для парного регрессионного анализа данные (Y и выбранная факторная переменные для всех рассматриваемых результатов наблюдений) переносятся на лист «ПарРег».
2.3. Нахождение оценок параметров уравнения парной регрессии осуществляется по формулам:
где Выборочный коэффициент детерминации можно найти по одной из формул:
Порядок выполнения работы: Расчет рекомендуется оформлять в виде таблиц, заголовки столбцов которых введены в строке 3 листа «ПарРег» рабочей книги. 6. Найти суммы и средние значения элементов столбцов D:M. Выборочные средние для Х и Y подсчитываются ниже таблицы с данными либо делением суммы значений результатов наблюдений, либо с помощью функции СРЗНАЧ. 7. Заполнить столбцы F:J. 8. Оценки параметров уравнения парной регрессии подсчитайте в ячейках R7, T7. 9. В столбце K подсчитайте оценки значений Y: 10. В ячейках G70, L70, N70 найти суммы квадратов Q, Q2, Q1, используя функцию СУММКВ 11. В ячейке V7 найдите значение R2. 12. Постройте график зависимости Y и
2.4. В случае, когда рассматривается зависимость между двумя переменными самый простой способ нахождения уравнения регрессии – вставка тренда на график функции.
13. Используя график, построенный в п. 2.3 (п.12), выполните следующие действия:
- На экране: график выделен метками.
- Диаграмма, Вставка линии тренда— На экране: диалоговое окно Линия тренда, ярлычок Тип
Характеристики каждого типа регрессии приведены в таблице
- Исходя из того, что рассматривается линейная регрессия, выбираем Линейная.
- На экране: диалоговое окно Линия тренда, Параметры
- ОК. - Уравнение регрессии для наглядности можно выделить жирным шрифтом и переместить в середину графика.
2.6. Нахождение оценок параметров уравнения как парной, так и множественной регрессии можно производить, используя функцию ЛИНЕЙН мастера функций. Функция рассчитывает статистику для ряда с применением метода наименьших квадратов, вычисляя прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Уравнение для прямой линии имеет следующий вид: y = bx + b0 или y = b1x1 + b2x2 +... + b0 (в случае нескольких интервалов значений x), где зависимое значение y является функцией независимого значения x. Значения b - это коэффициенты, соответствующие каждой независимой переменной x, а b0 - это постоянная. Заметим, что y, x и b могут быть векторами. Функция ЛИНЕЙН возвращает массив { bn; bn-1;...; b1; b0 }. ЛИНЕЙН может также возвращать дополнительную регрессионную статистику. Синтаксис: ЛИНЕЙН (Y; M; конст; статистика)
Y = b 0 + b1X1+…+bnXn M - это множество значений X, которые известны конст - это логическое значение, которое указывает, требуется ли, чтобы константа a0 была равна 0. (конст =1), статистика - это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии (статистика =1).
Дополнительная регрессионая статистика:
Для определения уровня надежности модели нужно сравнить табличные значения критической точки F-статистики (функция FРАСПОБР с заданным уровнем значимости и k-1, n-k степенями свободы, k –число переменных в уравнении, n –число наблюдений), со значением, возвращаемой функцией ЛИНЕЙН. В приведенной выше таблице показано, в каком порядке возвращается дополнительная регрессионная статистика. 14. Получить оценки параметров парной регрессии и ее характеристики, используя функцию ЛИНЕЙН (в ячейках Q40 R44). 15. Найти значения t-статистик для параметров уравнения, равной отношению оценки коэффициента регрессии к его стандартному отклонению (в ячейках Q46 R46).. Найти критические значение F-статистики (в ячейке U44). и t- статистики (в ячейке U45). с уровнем значимости 0,01. (Наличия линейной связи между переменными нельзя отрицать при Fф > F e, где F e - значение F-распределения Фишера с (k-1, n-k) степенями свободы). 16. Сделать выводы о значимости (незначимости) уравнения регрессии и параметра β (в ячейке Р50). 2.5. Нахождение оценок параметров уравнения парной регрессии можно производить с помощью матричных операций. Для этого вводятся матрицы результатов наблюдений, имеющие в нашем случае вид: Y = С помощью метода наименьших квадратов можно получить оценку b для коэффициентов регрессии b:
где (X т X)-1 - матрица, обратная матрице X т X, которая, по предположению, существует. Порядок выполнения работы: 17. Для реализации указанного метода столбец С расчетного листа «ПарРег» заполняем единицами (если он был занят – вставить столбец). 18. Для упрощения работы и облегчения выполнения действий с матрицами воспользуемся технологией присвоения имен диапазонам ячеек. Для этого выделите диапазон ячеек, в котором размещена матрица, затем выберите в меню ВставкаЮИмяЮПрисвоить. В появившемся диалоговом окне в поле Имя введите имя Y, Х. Присвоенное имя можно использовать в качестве ссылки на поименованные данные. Можно присвоить имя и объему выборки n. 19. Тогда, например, для вычисления оценок параметров в соответствующую ячейку достаточно ввести формулу
Формулы вводятся постепенно с использованием редактора формул. 20. Коэффициент детерминации задается формулой
Рекомендуется при вычислении R2 отдельно подсчитать числитель и знаменатель, используя операции над матрицами. Для справки при вводе функций можно пользоваться примером расчета, представленном на листе «ПарРег ПРИМЕР» 21. Для проверки значимости полученного уравнения регрессии вычисляется значение F-статистики Fф, подчиняющейся распределению Фишера: Fф 2.6. Нахождение доверительных интервалов параметров уравнения парной регрессии с надежностью (1-ε) заключается в определении точности оценок и нижних и верхних границ параметров: Δα=Sα·tкр(ε/2; n-k) и Δβ= Sβ·tкр(ε/2; n-k) αнижн =α-Δα; αверх =α+Δα βнижн =β-Δβ; βверх =β+Δβ 22. В ячейках Q86, Q87 найти точности оценок параметров, а в ячейках Q89-Q90, Т89-Т90 их нижние и верхние границы с надежностью 0,99. 23. Для проверки значимости полученного уравнения регрессии вычисляется значение F-статистики Fф, подчиняющейся распределению Фишера: 2.7. Проверка уровня значимости уравнения и коэффициентов при факторных переменных производится нахождением вероятности, с которой соответствующий критерий проверки гипотезы принимает фактическое значение. Для этого используются функции FРАСП(Fфакт; k;n-k) СТЬЮДРАСП(tфакт; n-k;2) 24. Определить уровень значимости уравнения и параметра β.
Замечания 1*. Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных. 2*. Значимость факторных переменных в уравнении регрессии проверяется сравнением t-статистики, равной отношению оценки коэффициента регрессии к его стандартному отклонению, с ее критическим значением tкр, определяемым по таблицам или с помощью функции СТЬЮДРАСПОБР с заданным уровнем значимости и (n-k) степенями свободы. Незначимые переменные следует исключить из уравнения.
КОЛОМЕНСКИЙ ИНСТИТУТ (ФИЛИАЛ)
|

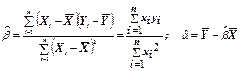
 ,
, 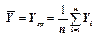 ,
, 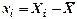 ,
, 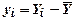 .
.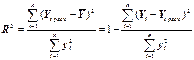
 (
( ), в столбце L – их отклонения от результатов наблюдений, в столбце M – квадраты отклонений, в столбце N – отклонения оценок от средних.
), в столбце L – их отклонения от результатов наблюдений, в столбце M – квадраты отклонений, в столбце N – отклонения оценок от средних.
 от Х (по данным в столбцах D, E, K), используя мастер диаграмм (тип диаграммы – Точечная без соединяющих отрезков). Введите название диаграммы (зависимость каких показателей рассматривается), легенду (названия столбцов, использовавшихся при построении графика) и размерности показателей.
от Х (по данным в столбцах D, E, K), используя мастер диаграмм (тип диаграммы – Точечная без соединяющих отрезков). Введите название диаграммы (зависимость каких показателей рассматривается), легенду (названия столбцов, использовавшихся при построении графика) и размерности показателей. - Курсор на график.
- Курсор на график.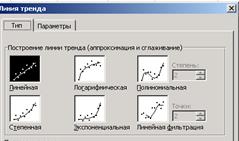
 - Курсор на ярлычок Параметры.
- Курсор на ярлычок Параметры. - Назначаем: Показывать уравнение на диаграмме, Поместить на диаграмму R2.
- Назначаем: Показывать уравнение на диаграмме, Поместить на диаграмму R2.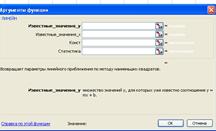 Y - это множество значений Y, которые уже известны для соотношения
Y - это множество значений Y, которые уже известны для соотношения
 ; X =
; X = 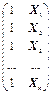 ; и оценок параметров уравнения: b =
; и оценок параметров уравнения: b =  .
. = (X т X)-1 Xт Y
= (X т X)-1 Xт Y