Понятие евклидова пространства. Неравенство Коши-Буняковского ЛЕКЦИИ ПО ДИСЦИПЛИНЕ
«ЛИНЕЙНАЯ АЛГЕБРА»
Направление 080100
«Экономика»
Очная форма обучения
Пусть задано линейное пространство. Возникает вопрос: можно ли измерять расстояние между элементами (векторами) этого пространства, находить углы между векторами и длины (модули) этих векторов. Ответы на этот вопрос дает понятие евклидова линейного пространства. Определение 3.1. Если в линейном пространстве
то это пространство называется евклидовым пространством. Число Аксиома Поскольку евклидово пространство является линейным, то на него переносятся все понятия, определенные для линейного пространства. В частности, можно ввести понятие базиса и размерности евклидова пространства. Сформулируем простейшие следствия из аксиом евклидова пространства: 1) 2) 3) Теорема 3.1. В евклидовом пространстве
□ Отбрасывая тривиальный случай, когда один из векторов
Преобразовав скалярное произведение согласно аксиомам, получим
Левую часть полученного неравенства можно рассматривать как квадратный трехчлен относительно
откуда и следует неравенство (3.1). ■
|

 любым двум элементам
любым двум элементам  можно поставить в соответствие действительное число
можно поставить в соответствие действительное число 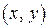 , называемое скалярным произведением векторов
, называемое скалярным произведением векторов  и удовлетворяющее аксиомам:
и удовлетворяющее аксиомам:
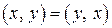 ,
,
 ,
,  ,
,
 ,
,  ,
,
 , причем
, причем 
 ,
, называется скалярным квадратом вектора
называется скалярным квадратом вектора 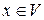 .
. определяет симметричность скалярного произведения, аксиомы
определяет симметричность скалярного произведения, аксиомы 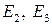 – аддитивность и однородность по первому множителю,
– аддитивность и однородность по первому множителю, 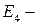 неотрицательность скалярного квадрата.
неотрицательность скалярного квадрата. ,
,  ,
,
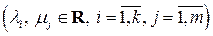 ,
, .
. для любых двух векторов
для любых двух векторов 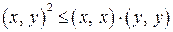 . (3.1)
. (3.1) . Рассмотрим при произвольном числе
. Рассмотрим при произвольном числе  и найдем его скалярный квадрат
и найдем его скалярный квадрат .
.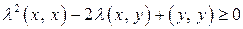 .
. ), принимающий неотрицательные значения при каждом
), принимающий неотрицательные значения при каждом  ,
,


