1. Является ли заданное отображение  на своей естественной области определения непрерывным в точке
на своей естественной области определения непрерывным в точке  ?
?
Пример 1.  ,
,  ,,
,,  .
.
Решение. Очевидно, что заданное отображение определено на всем  . Представим его в виде
. Представим его в виде  , где
, где  ,
, 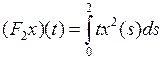 , и покажем, что
, и покажем, что  и
и  непрерывны в любой точке
непрерывны в любой точке 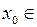
 . Пусть последовательность
. Пусть последовательность  сходится к
сходится к  в
в  . Тогда
. Тогда


 .
.
Отсюда следует, что  непрерывно.
непрерывно.
Докажем непрерывность  . Будучи непрерывной, функция
. Будучи непрерывной, функция 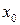 ограничена на
ограничена на  , т. е.
, т. е. 

 . А так как
. А так как  равномерно на
равномерно на  , то начиная с некоторого номера
, то начиная с некоторого номера 
 (почему?). Тогда
(почему?). Тогда




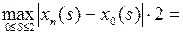


 .
.
Отсюда следует, что 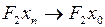 в
в  . Поэтому в силу произвольности
. Поэтому в силу произвольности  отображение
отображение  непрерывно в любой точке из
непрерывно в любой точке из  .
.
Пример 2. 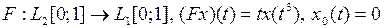 .
.
Решение. Пусть последовательность  сходится к
сходится к  в
в  . Тогда
. Тогда

 при
при  .
.
Теперь в силу неравенства Коши-Буняковского,



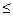
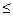

 .
.
(полученная оценка показывает также, что  принадлежит
принадлежит  при
при 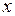 из
из  ; поэтому отображение
; поэтому отображение  определено на всем
определено на всем  ). Значит,
). Значит,  – непрерывное отображение в точке
– непрерывное отображение в точке  .
.
Пример 3.  .
.
Решение. Покажем, что отображение не является непрерывным. Возьмём последовательность 
 , которая стремится к нулюв
, которая стремится к нулюв  , поскольку
, поскольку

 при
при  .
.
Рассмотрим теперь выражение

 .
.
Следовательно, последовательность  нестремится к нулю при
нестремится к нулю при  ,а потому
,а потому  нестремится к
нестремится к  в
в  .
.
Пример 4.  .
.
Решение. Покажем, что отображение не является непрерывным. Заметим, что



 .
.
Возьмем последовательность  , которая сходится к нулю в
, которая сходится к нулю в  , поскольку
, поскольку
 при
при  .
.
Имеем
 при
при  ,
,
а потому  нестремится к
нестремится к  в
в  .
.
2. Является ли заданное отображение  : а) непрерывным;
: а) непрерывным;
б) равномерно непрерывным; в) удовлетворяющим условию Липшица?
Пример 1.  .
.
Решение. а) Пусть  . Отображение
. Отображение  является непрерывным, так как
является непрерывным, так как

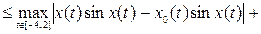
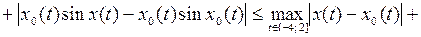
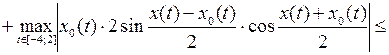
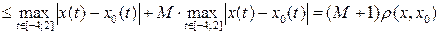
(мы воспользовались неравенством  ).
).
б) Покажем, что  не является равномерно непрерывным. Возьмём
не является равномерно непрерывным. Возьмём  . Тогда
. Тогда 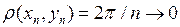 при
при  , но
, но

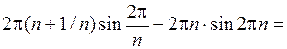
 ,
,
а значит,  не стремится к нулю при
не стремится к нулю при  . Это противоречит определению равномерной непрерывности (проверьте).
. Это противоречит определению равномерной непрерывности (проверьте).
в) Так как  не является равномерно непрерывным, то оно не удовлетворяет условию Липшица (почему?).
не является равномерно непрерывным, то оно не удовлетворяет условию Липшица (почему?).
Пример 2.  .
.
Решение. Покажем, что  удовлетворяет условию Липшица с константой
удовлетворяет условию Липшица с константой  . Заметим, что
. Заметим, что

 .
.
Рассмотрим функцию  . Тогда
. Тогда
 .
.
Следовательно, по теореме Лагранжа
 ,
,
а значит,

 .
.
Так как  удовлетворяет условию Липшица, то оно равномерно непрерывно, а потому и непрерывно.
удовлетворяет условию Липшица, то оно равномерно непрерывно, а потому и непрерывно.
Пример 3.  .
.
Решение. Покажем, что  удовлетворяет условию Липшица. Действительно,
удовлетворяет условию Липшица. Действительно,


 Так как
Так как  , то по теореме Лагранжа
, то по теореме Лагранжа
 .
.
Поэтому при любых x, y справедливо неравенство
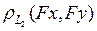
 .
.
Так как  удовлетворяет условию Липшица, то оно является равномерно непрерывным.
удовлетворяет условию Липшица, то оно является равномерно непрерывным.
Пример 4.  .
.
Решение. а) Покажем, что  непрерывно. Действительно, если
непрерывно. Действительно, если  в
в  , то числоваяпоследовательность
, то числоваяпоследовательность  сходится к
сходится к  (почему?). Тогда
(почему?). Тогда
 при
при  .
.
б) Покажем, что  не является равномерно непрерывным. Пусть последовательности
не является равномерно непрерывным. Пусть последовательности 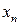 и
и  заданы следующим образом:
заданы следующим образом:
 ,
, 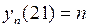 ,
,  ,
,  .
.
Тогда

 при
при  ,
,
но

 при
при  .
.
в) Так как  не является равномерно непрерывным, то оно не удовлетворяет и условию Липшица.
не является равномерно непрерывным, то оно не удовлетворяет и условию Липшица.
Пример 5.  .
.
Решение. а) Покажем, что  не удовлетворяет условию Липшица. Допустим противное, то есть что
не удовлетворяет условию Липшица. Допустим противное, то есть что

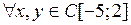
 .
.
Возьмем  . Так как
. Так как
 (1)
(1)
то  , то есть
, то есть  ,
,  . Противоречие.
. Противоречие.
б) Покажем, что  является равномерно непрерывным. Заметим, что функция
является равномерно непрерывным. Заметим, что функция  является равномерно непрерывной на
является равномерно непрерывной на  . Действительно, она равномерно непрерывна на
. Действительно, она равномерно непрерывна на  по теореме Кантора и равномерно непрерывна на
по теореме Кантора и равномерно непрерывна на  по теореме Лагранжа, так как
по теореме Лагранжа, так как  при
при  . Равномерная непрерывность функции
. Равномерная непрерывность функции  означает, что
означает, что

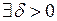

 .
.
Теперь, если  , то
, то 
 . Поэтому в силу равенства (1)
. Поэтому в силу равенства (1)
 .
.

 на своей естественной области определения непрерывным в точке
на своей естественной области определения непрерывным в точке  ?
? ,
,  ,,
,,  .
. . Представим его в виде
. Представим его в виде  , где
, где  ,
, 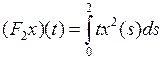 , и покажем, что
, и покажем, что  и
и  непрерывны в любой точке
непрерывны в любой точке 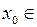
 сходится к
сходится к  в
в 

 .
.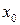 ограничена на
ограничена на  , т. е.
, т. е. 

 . А так как
. А так как  равномерно на
равномерно на 




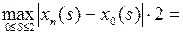


 .
.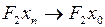 в
в  . Поэтому в силу произвольности
. Поэтому в силу произвольности  непрерывно в любой точке из
непрерывно в любой точке из 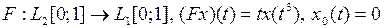 .
. сходится к
сходится к  . Тогда
. Тогда
 при
при  .
.


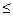

 .
. принадлежит
принадлежит 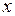 из
из  .
.
 , которая стремится к нулюв
, которая стремится к нулюв 
 при
при  .
.
 .
. нестремится к нулю при
нестремится к нулю при  нестремится к
нестремится к  в
в  .
. .
.


 .
. , которая сходится к нулю в
, которая сходится к нулю в  при
при  при
при  .
. . Отображение
. Отображение 
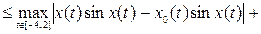
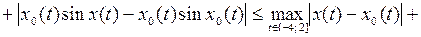
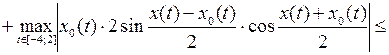
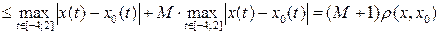
 ).
). . Тогда
. Тогда 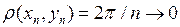 при
при 
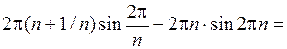
 ,
, не стремится к нулю при
не стремится к нулю при  .
. . Заметим, что
. Заметим, что
 .
. . Тогда
. Тогда .
. ,
,
 .
. .
.

 Так как
Так как  , то по теореме Лагранжа
, то по теореме Лагранжа .
.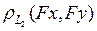
 .
. .
. в
в  , то числоваяпоследовательность
, то числоваяпоследовательность  сходится к
сходится к  (почему?). Тогда
(почему?). Тогда при
при 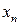 и
и  заданы следующим образом:
заданы следующим образом: ,
, 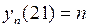 ,
,  ,
,  .
.
 при
при 
 при
при  .
.
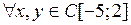
 .
. . Так как
. Так как (1)
(1) , то есть
, то есть  ,
,  . Противоречие.
. Противоречие. является равномерно непрерывной на
является равномерно непрерывной на  . Действительно, она равномерно непрерывна на
. Действительно, она равномерно непрерывна на  по теореме Кантора и равномерно непрерывна на
по теореме Кантора и равномерно непрерывна на  по теореме Лагранжа, так как
по теореме Лагранжа, так как  при
при  . Равномерная непрерывность функции
. Равномерная непрерывность функции 
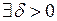

 .
. , то
, то 
 . Поэтому в силу равенства (1)
. Поэтому в силу равенства (1) .
.


