Пусть  - нормированное пространство,
- нормированное пространство,  - замкнутое подпространство. Рассмотрим фактор-пространство
- замкнутое подпространство. Рассмотрим фактор-пространство 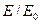 . В силу замкнутости
. В силу замкнутости  класс
класс 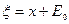 - замкнутое множество в
- замкнутое множество в  .
.
Если для  положить
положить
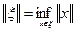 , (3.7)
, (3.7)
то 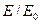 превратится в нормированное пространство. Проверим справедливость аксиом нормированного пространства.
превратится в нормированное пространство. Проверим справедливость аксиом нормированного пространства.
Если 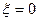 , то в качестве
, то в качестве 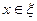 можно взять нулевой элемент пространства
можно взять нулевой элемент пространства  и поэтому
и поэтому  . Обратно, если
. Обратно, если  , то согласно (3.7) и по свойству нижней грани существует последовательность
, то согласно (3.7) и по свойству нижней грани существует последовательность 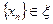 , такая что
, такая что 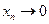 . И поскольку класс
. И поскольку класс  - замкнут, то содержит предельную точку:
- замкнут, то содержит предельную точку:  и тем самым
и тем самым  является нулевым элементом фактор-пространства
является нулевым элементом фактор-пространства 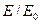 .
.
Проверим однородность нормы, рассматривая случай 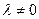 . Имеем
. Имеем
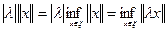 .
.
Когда  пробегает класс
пробегает класс  , элемент
, элемент  пробегает класс
пробегает класс 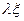 , откуда следует, что
, откуда следует, что
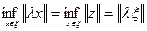 .
.
Теперь докажем неравенство треугольника. Для произвольных 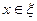 ,
, 
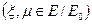 имеем
имеем 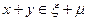 , поэтому
, поэтому
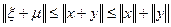 .
.
Переходя в правой части к точным нижним граням, получим неравенство треугольника.
Далее докажем, что если  - полное пространство, то и фактор-пространство
- полное пространство, то и фактор-пространство 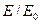 - полно. Вначале заметим, что согласно (3.7) для каждого
- полно. Вначале заметим, что согласно (3.7) для каждого  найдется такой элемент
найдется такой элемент 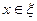 , что
, что
 . (3.8)
. (3.8)
А теперь возьмем фундаментальную последовательность  в пространстве
в пространстве 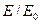 . Переходя, если нужно к подпоследовательности, можно считать, что ряд
. Переходя, если нужно к подпоследовательности, можно считать, что ряд
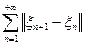
сходится. Способ построения указанной подпоследовательности приведен в теореме 2. К последовательности  добавим еще
добавим еще 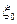 - нулевой элемент пространства
- нулевой элемент пространства 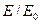 . Выберем
. Выберем 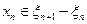 (
( ) так, что
) так, что
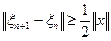 .
.
Тогда ряд 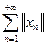 сходится и по теореме 2 в силу полноты пространства
сходится и по теореме 2 в силу полноты пространства  сходится такжеряд
сходится такжеряд 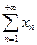 . Положим
. Положим 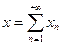 и обозначим через
и обозначим через  , содержащий
, содержащий  . Поскольку при каждом
. Поскольку при каждом  справедливо включение
справедливо включение  , то
, то
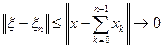 , при
, при 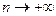 ,
,
т.е. 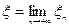 . Таким образом доказана теорема.
. Таким образом доказана теорема.
Теорема 5. Фактор – пространство банахова пространства по любому его подпространству есть банахово пространство.

 - нормированное пространство,
- нормированное пространство,  - замкнутое подпространство. Рассмотрим фактор-пространство
- замкнутое подпространство. Рассмотрим фактор-пространство 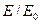 . В силу замкнутости
. В силу замкнутости 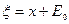 - замкнутое множество в
- замкнутое множество в  положить
положить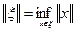 , (3.7)
, (3.7)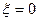 , то в качестве
, то в качестве 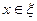 можно взять нулевой элемент пространства
можно взять нулевой элемент пространства  . Обратно, если
. Обратно, если 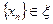 , такая что
, такая что 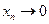 . И поскольку класс
. И поскольку класс  - замкнут, то содержит предельную точку:
- замкнут, то содержит предельную точку:  и тем самым
и тем самым 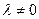 . Имеем
. Имеем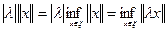 .
. пробегает класс
пробегает класс  пробегает класс
пробегает класс 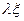 , откуда следует, что
, откуда следует, что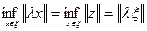 .
.
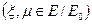 имеем
имеем 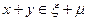 , поэтому
, поэтому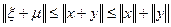 .
. . (3.8)
. (3.8) в пространстве
в пространстве 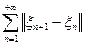
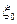 - нулевой элемент пространства
- нулевой элемент пространства 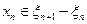 (
( ) так, что
) так, что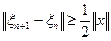 .
.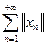 сходится и по теореме 2 в силу полноты пространства
сходится и по теореме 2 в силу полноты пространства 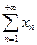 . Положим
. Положим 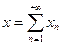 и обозначим через
и обозначим через  справедливо включение
справедливо включение  , то
, то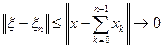 , при
, при 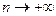 ,
,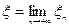 . Таким образом доказана теорема.
. Таким образом доказана теорема.


