Условия интегрируемости (по Риману) функции двух переменных
Теорема 1 (необходимое условие интегрируемости). Если функция f(x; y) интегрируема на простом компакте D, то она ограничена на этом компакте. à Проведем доказательство методом от противного. Пусть существует функция f(x; y) интегрируемая на простом компакте D, но неограниченная на этом компакте. Тогда при любом разбиении Т на любое конечное число n ячеек (D Sk) с площадями D Sk ( f(x; y) не ограничена хотя бы в одной из этих ячеек. Пусть, например, f(x; y) не ограничена в (D S1). В остальных ячейках (D Sk) возьмем произвольные точки Пусть
В силу неограниченности функции f(x; y) в ячейке (D S1) найдется точка Тогда для соответствующей интегральной суммы
Отсюда следует, что при При доказательстве следующей теоремы нам понадобится понятие сумм Дарбу. Пусть f(x; y) – ограниченная на простом компакте D функция и T – произвольное разбиение этого компакта на частичные ячейки (D Sk) (
Составим суммы
Эти суммы будем называть соответственно нижней и верхней суммами Дарбу функции f(x; y) для данного разбиения T компакта D. Очевидно, что Легко видеть, что: 1) Для одного и того же разбиения T любая интегральная сумма s(T) заключена между нижней и верхней суммами Дарбу: 2) Если функция f(x; y) непрерывна на компакте D, то суммы Дарбу (1) являются интегральными суммами этой функции при любом разбиении T компакта D. Отметим следующие свойства сумм Дарбу(доказательство этих свойств аналогично доказательству их свойств для функции одной переменной): Свойство 1. При данном (фиксированном) разбиении T компакта D суммы Дарбу
Свойство 2. Если разбиение T1 компакта D получено из разбиения T добавлением конечного числа новых ячеек, то
при добавлении новых ячеек нижняя сумма Дарбу может лишь увеличиться, а верхняя сумма Дарбу – лишь уменьшиться. Свойство 3. Любая нижняя сумма Дарбу для функции на компакте не превосходит любой верхней суммы Дарбу (независимо от того, соответствуют ли эти суммы одному разбиению или различным разбиениям компакта D.) Следствие. Множество Числа I1 и I2 называются соответственно нижним и верхним интегралами функции f(x; y) на компакте D. Теорема 2 (необходимое и достаточное условие интегрируемости). Для того, чтобы ограниченная на простом компакте D функция f(x; y) была интегрируема на этом компакте, необходимо и достаточно, чтобы à Необходимость. Пусть f (x; y) интегрируема на D, т.е. существует двойной интеграл
или короче
Требуется показать, что
Действительно, в силу (1) имеем
При любом фиксированном разбиении T согласно первому свойству сумм Дарбу имеем:
Поэтому существуют интегральные суммы s1 и s2, принадлежащие множеству С другой стороны, на основании последнего неравенства цепочки (7) имеем:
Из (8) и (9) следует, что
т.е.
Из двух последних неравенств получаем:
Таким образом, цепочка (6) выполняется при d, указанном в цепочке (7). Достаточность. Пусть
Покажем, что функция f (x; y) интегрируема на компакте D. Воспользуемся неравенствами (4): Откуда
а так как Положим
С другой стороны, для любой интегральной суммы
Из (11) и (12) получаем:
Отсюда, с учетом (10), следует, что существует конечный предел Теорема 3 (достаточное условие интегрируемости). Если функция f (x; y) непрерывна на компакте D, то она интегрируема на этом компакте. àПусть f (x; y) непрерывна на простом компакте D, а m и M – ее наибольшее и наименьшее значения в D. Разобьем компакт D произвольным образом на любое конечное число n квадрируемых ячеек (D Sk) ( (D Sk) и принимает (D Sk) в наименьшее и наибольшее значения mk и Mk соответственно ( Тогда
Пусть S – площадь компакта D. Так как f (x; y) непрерывна на компакте D, то она равномерно-непрерывна на этом компакте. Поэтому, для любого Пусть
Поэтому
Таким образом, для любого
Это и значит, что Следовательно, на основании теоремы 2 заключаем, что функция f (x; y) интегрируема в D. ¨ Замечание 1. Можно показать, что ограниченная на простом компакте D функция f (x; y) интегрируема на этом компакте, если она имеет разрыв в конечном числе точек из D, и (или) на конечном числе линий, имеющих нулевую площадь, двойной интеграл не изменится, если подинтегральную функцию произвольным образом переопределить на указанных выше линиях или в этих точках. Замечание 2. Из задачи §1 с учетом теоремы 3 вытекает следующее утверждение, выражающее физический смысл двойного интеграла: Двойной интеграл по простому компакту D от непрерывной и неотрицательной на D функции f (x; y) равен массе материальной пластины D с поверхностной плотностью f (x; y):
|

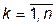 ) функция
) функция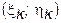 (
( ).
). .
.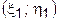 такая, что
такая, что  .
. будем иметь
будем иметь .
.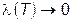 не существует конечного предела интегральной суммы s, что противоречит интегрируемости функции f(x; y) в D. ¨
не существует конечного предела интегральной суммы s, что противоречит интегрируемости функции f(x; y) в D. ¨
 . (1)
. (1)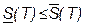 .
. (2)
(2) функции f(x; y) являются соответственно ТН и ТВ гранями множества
функции f(x; y) являются соответственно ТН и ТВ гранями множества  всех интегральных сумм (для функции f(x; y)) на компакте D, соответствующих этому же разбиению T компакта D:
всех интегральных сумм (для функции f(x; y)) на компакте D, соответствующих этому же разбиению T компакта D: . (3)
. (3) 
 , т.е.
, т.е.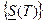 всех нижних сумм Дарбу функции f(x; y) на компакте D (соответствующих всевозможным разбиениям компакта) имеет конечную точную верхнюю грань
всех нижних сумм Дарбу функции f(x; y) на компакте D (соответствующих всевозможным разбиениям компакта) имеет конечную точную верхнюю грань 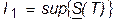 , а множество
, а множество  всех верхних сумм Дарбу имеет конечную точную нижнюю грань
всех верхних сумм Дарбу имеет конечную точную нижнюю грань  , причем
, причем 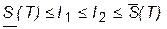 . (4)
. (4)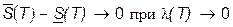 , где
, где 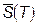 и
и 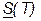 - соответственно верхняя и нижняя суммы Дарбу функции f (x; y), соответствующие разбиению T компакта D.
- соответственно верхняя и нижняя суммы Дарбу функции f (x; y), соответствующие разбиению T компакта D.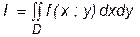
 . (5)
. (5)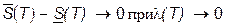 , т.е., что
, т.е., что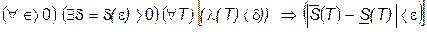 . (6)
. (6) . (7)
. (7) .
. ,такие, что
,такие, что  . (8)
. (8) . (9)
. (9)
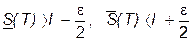 .
.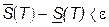 , или
, или  .
.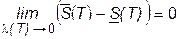 . (10)
. (10) ,
,
 и, следовательно, с учетом (10) на основании «принципа двух милиционеров» получаем:
и, следовательно, с учетом (10) на основании «принципа двух милиционеров» получаем:
 , то
, то  0 или
0 или 
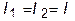 .Тогда неравенство (4) примет вид:
.Тогда неравенство (4) примет вид: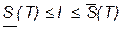 . (11)
. (11) имеем:
имеем: . (12)
. (12)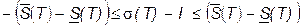 .
.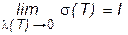 . Это и означает, что функция f (x; y) интегрируема в D. ¨
. Это и означает, что функция f (x; y) интегрируема в D. ¨ .
.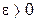 , а значит, и для
, а значит, и для 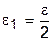 найдется
найдется 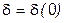 , такое, что
, такое, что  . (13)
. (13)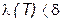 . Тогда в каждой ячейке (D Sk) найдутся две точки
. Тогда в каждой ячейке (D Sk) найдутся две точки 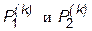 такие, что
такие, что . Следовательно, в силу (13) будем иметь
. Следовательно, в силу (13) будем иметь .
.
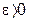 мы нашли
мы нашли 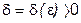 (см. цепочку (10¢) такое, что
(см. цепочку (10¢) такое, что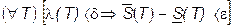 .
. .
.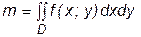 .
.


