40. 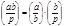
Следствие.  .
.
50. 
Следствие. Если 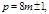 то
то  .Если
.Если 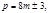 то
то  Поэтому
Поэтому 
60. (Закон взаимности) Если  и
и 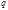 нечётные простые числа, то, или
нечётные простые числа, то, или 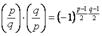 Или
Или
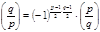 . (11)
. (11)
Следствие. Если хотя бы одно из чисел 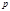 или
или 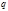 имеет форму
имеет форму  , то показатель в правой части (11) чётный, и
, то показатель в правой части (11) чётный, и  . Если и
. Если и  или
или  имеет форму
имеет форму 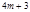 , то показатель в правой части (11) нечётный, и
, то показатель в правой части (11) нечётный, и 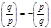 .
.
41 Символ Якоби и его свойства.
Определение. Пусть нечётное число 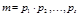 , где
, где 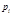 - простые числа, среди которых могут быть одинаковые,
- простые числа, среди которых могут быть одинаковые, 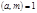 .Символ Якоби определяется равенством
.Символ Якоби определяется равенством  , (12)
, (12)
Где 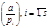 - символы Лежандра.Читается
- символы Лежандра.Читается 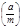 - «символ Якоби
- «символ Якоби  по отношению к
по отношению к 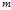 ».
».
Замечание1. символ Лежандра является частным случаем символа Якоби.
Замечание2. символ Якоби обладает свойствами 10-60 символа Лежандра с той лишь разницей, что в случае символа Якоби речь идёт не о нечётных простых числах 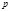 , а о нечётных числах
, а о нечётных числах  .Из замечаний следует, что при вычислении символа Лежандра удобно рассматривать его как символ Якоби, тогда отпадает необходимость выделять из числителя его нечётные простые множители.По значению символа Якоби можно сказать следующее:
.Из замечаний следует, что при вычислении символа Лежандра удобно рассматривать его как символ Якоби, тогда отпадает необходимость выделять из числителя его нечётные простые множители.По значению символа Якоби можно сказать следующее:
- если  , то
, то  - квадратичный невычет по
- квадратичный невычет по 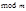 ;- если
;- если 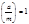 и
и 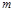 - нечётное составное число, то о квадратичности вычета
- нечётное составное число, то о квадратичности вычета  по
по 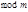 ничего сказать нельзя.
ничего сказать нельзя.
Свойства
10. Если  то
то  .
.
20. 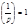 , т.е. 1 – квадратичный вычет для любого нечётного простого
, т.е. 1 – квадратичный вычет для любого нечётного простого 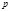 , т.к. сравнение
, т.к. сравнение  всегда разрешимо.
всегда разрешимо.
30. 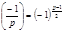
Следствие. 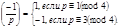
40. 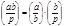
Следствие.  .
.
50. 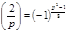





 42 Сравнения второй степени по составному модулю
42 Сравнения второй степени по составному модулю
Рассмотрим сравнение по составному модулю
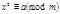 . (13)
. (13)
Если 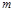 - чётное, то справедлива теорема
- чётное, то справедлива теорема
Теорема Пусть  , где
, где 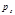 - различные нечётные простые числа,
- различные нечётные простые числа, 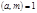 . Сравнение (13) имеет решения тогда и только тогда, когда
. Сравнение (13) имеет решения тогда и только тогда, когда
1.  - квадратичный вычет по всем модулям
- квадратичный вычет по всем модулям  2. если
2. если 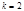 , то
, то 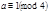 , а если
, а если 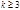 , то
, то 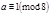 .
.
Число решений сравнения (13) (если они существуют) равно
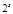 при
при 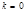 и
и 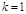 ;
;
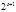 при
при 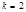 ;
;
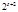 при
при 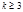 .
.
Доказательство. Сравнение (13) равносильно системе
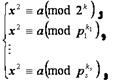 (14)
(14)
Если 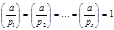 , то
, то
1) при  и
и  первое сравнение (14) имеет одно решение, каждое последующее сравнение имеет по два решения. Тогда система (14) и сравнение (13) имеет
первое сравнение (14) имеет одно решение, каждое последующее сравнение имеет по два решения. Тогда система (14) и сравнение (13) имеет 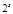 решений;
решений;
2) при 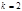 и
и 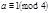 каждое сравнение в (14) имеет по два решения. Тогда система (14) и сравнение (13) имеет
каждое сравнение в (14) имеет по два решения. Тогда система (14) и сравнение (13) имеет 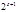 решений;
решений;
3) при 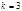 ,
, 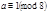 первое сравнение имеет
первое сравнение имеет  решения (доказать самостоятельно). Тогда система (14) и сравнение (13) имеет
решения (доказать самостоятельно). Тогда система (14) и сравнение (13) имеет 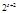 решений.
решений.
Во всех остальных случаях, т.е. если
1) хотя бы один из символов Лежандра 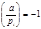 ;
;
3) при 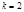
 ;
;
4) при 
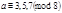 ;
;
в систему (14) входят сравнение, которое не имеет решения, а следовательно, не имеет решений и сравнение (13).
В случае нечётного 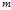 сравнение (13) можно исследовать с помощью символа Якоби
сравнение (13) можно исследовать с помощью символа Якоби 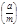 . Однако, если
. Однако, если 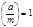 ничего о числе решений мы сказать не можем.
ничего о числе решений мы сказать не можем.
Справедлива также теорема:
Теорема Сравнение 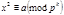 (где
(где 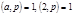 ) имеет два решения, если
) имеет два решения, если  и не имеет решений, если
и не имеет решений, если 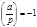 . (без доказательства).
. (без доказательства).
43 Показатели и их основные свойства.
Сравнение вида 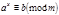 называется показательным. Изучение таких сравнений сводится к изучению сравнений вид
называется показательным. Изучение таких сравнений сводится к изучению сравнений вид  . (1)
. (1)
Если 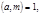 то по теореме Эйлера
то по теореме Эйлера  следовательно сравнение (1) при
следовательно сравнение (1) при 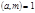 всегда имеет решение.
всегда имеет решение.
Определение. Наименьшее положительное решение  сравнения (1) называется показателем числа
сравнения (1) называется показателем числа  по модулю
по модулю  , или говорят, что число
, или говорят, что число  принадлежит показателю
принадлежит показателю 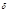 по модулю
по модулю  Записывают
Записывают  .
.
Определение. Числа, принадлежащие показателю 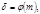 называются первообразными корнями по модулю
называются первообразными корнями по модулю 
Свойства показателей.
1. Числа одного класса вычетов принадлежат одному и тому же показателю.
Доказательство.
Пусть 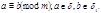 Т.к.
Т.к. 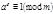 и
и 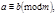 то
то  следовательно
следовательно  Т.к.
Т.к.  и
и 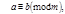 то
то 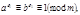 следовательно
следовательно  Отсюда
Отсюда 
2. Если 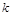 является решением сравнения (1) и
является решением сравнения (1) и  то
то 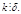
Доказательство.
На основе теоремы о делении с остатком  и
и  Т.к.
Т.к.  решение сравнения (1), то
решение сравнения (1), то 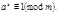 Тогда
Тогда 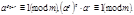
Т.к.  то
то  поэтому
поэтому 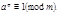 Но,
Но, 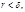 следовательно
следовательно  Таким образом,
Таким образом,  т. е.
т. е. 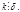
Следствие. Если  то
то 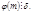
Доказательство.
По теореме Эйлера  т.е.
т.е.  решение сравнения (1). Следовательно,
решение сравнения (1). Следовательно, 
Замечание. Из сформулированного следствия получаем, что показатель числа  по модулю
по модулю  надо искать среди делителей
надо искать среди делителей 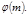
3. Сравнение 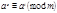 имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда  где
где 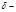 показатель числа
показатель числа  по модулю
по модулю 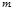
Доказательство.
1. Пусть  и для определённости
и для определённости 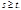 Т.к.
Т.к.  то
то 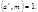 Сократим сравнение на
Сократим сравнение на 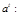
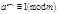 Тогда по свойству
Тогда по свойству 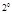
 следовательно,
следовательно, 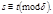
2. Пусть 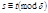 и
и  Тогда
Тогда 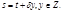 Получаем
Получаем 
4. Если 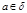 по модулю
по модулю 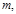 то числа
то числа 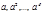 попарно не сравнимы по модулю
попарно не сравнимы по модулю 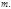
Доказательство. Согласно свойству 
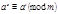 тогда и только тогда, когда
тогда и только тогда, когда 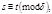 но среди показателей последовательности (2) нет сравнимых по модулю
но среди показателей последовательности (2) нет сравнимых по модулю 
44. Первообразные корни. Теорема о существовании первообразного корня по простому модулю.
Определение. Числа, принадлежащие показателю 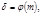 называются первообразными корнями по модулю
называются первообразными корнями по модулю 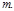
Лемма. По простому модулю  делитель
делитель  числа
числа  либо не является показателем какого-либо класса вычетов, либо является для
либо не является показателем какого-либо класса вычетов, либо является для 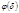 таких классов ( доказательство самостоятельно).
таких классов ( доказательство самостоятельно).
По простому модулю каждый делитель 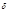 числа
числа  является показателем для
является показателем для 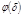 классов.
классов.
Теорема (Гаусса). По любому простому модулю 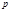 существует
существует  классов первообразных корней.
классов первообразных корней.
Доказательство. Пусть 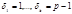 все делители числа
все делители числа 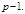 Распределяя вычеты приведённой системы вычетов по модулю
Распределяя вычеты приведённой системы вычетов по модулю 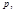 т.е. числа
т.е. числа 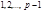 в отдельные группы по принадлежности своему показателю, всего должны получить
в отдельные группы по принадлежности своему показателю, всего должны получить  чисел.Если обозначить
чисел.Если обозначить 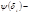 число чисел приведённой системы, принадлежащих показателю
число чисел приведённой системы, принадлежащих показателю 
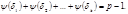 (3)
(3)
С другой стороны, сумма значений функций Эйлера, распространённая по всем делителям данного числа, равна этому числу, т.е.
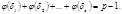 (4) Приравнивая (3) и (4), получаем
(4) Приравнивая (3) и (4), получаем 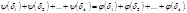 Согласно лемме
Согласно лемме 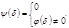 Отсюда в равенстве (5) всегда
Отсюда в равенстве (5) всегда 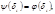 т.к. если хотя бы одно
т.к. если хотя бы одно  то в правой части (5) останется лишний положительный член и равенство нарушается. Тогда получаем, что для делителя
то в правой части (5) останется лишний положительный член и равенство нарушается. Тогда получаем, что для делителя  существует
существует 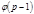 классов первообразных корней.
классов первообразных корней.
Замечание. Первообразные корни существуют только по модулям, 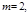

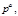
 где
где 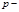 простое нечётное число,
простое нечётное число, 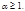
45.Первообразные корни по модулям 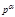 и
и 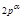 . Теорема об отыскании первообразных корней
. Теорема об отыскании первообразных корней
Пусть 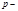 простое нечётное число и
простое нечётное число и 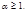 Первообразные корни по модулям
Первообразные корни по модулям 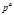 и
и 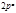 связаны следующим свойством:
связаны следующим свойством:
Свойство. Пусть 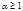 и
и 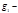 первообразный корень по модулю
первообразный корень по модулю 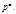 Нечётное из чисел
Нечётное из чисел 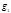 и
и 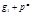 будет первообразным корнем по модулю
будет первообразным корнем по модулю  Первообразные корни по модулям
Первообразные корни по модулям 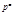 и
и 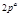 можно находить, пользуясь теоремой:
можно находить, пользуясь теоремой:
Теорема. Пусть 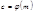 и
и 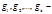 различные простые делители числа
различные простые делители числа  Для того, чтобы число
Для того, чтобы число 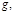 взаимно простое с модулем
взаимно простое с модулем 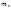 было первообразным корнем по модулю
было первообразным корнем по модулю 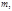 необходимо и достаточно, чтобы это
необходимо и достаточно, чтобы это 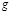 не удовлетворяло ни одному из сравнений
не удовлетворяло ни одному из сравнений 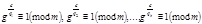 .
.
46.Индексы и их свойства. Индексы по модулям 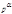 и
и 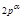 . Таблица индексов.
. Таблица индексов.
Пусть  первообразный корень по простому модулю
первообразный корень по простому модулю  тогда числа
тогда числа  представляют собой приведённую систему вычетов по модулю
представляют собой приведённую систему вычетов по модулю 
Так как для любого простого 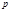 существуют первообразные корни, то приведённую систему вычетов можно составить указанным способом. Таким образом, для любого числа
существуют первообразные корни, то приведённую систему вычетов можно составить указанным способом. Таким образом, для любого числа  взаимно простого с
взаимно простого с  найдётся единственное число
найдётся единственное число 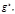 принадлежащее тому же классу по модулю
принадлежащее тому же классу по модулю  что и
что и 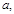 т.е.
т.е.  где
где 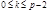 . Это позволяет ввести понятие индекса.
. Это позволяет ввести понятие индекса.
Определение. Пусть 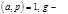 первообразный корень по модулю
первообразный корень по модулю  Если выполняется сравнение (7), то число
Если выполняется сравнение (7), то число  называется индексом числа
называется индексом числа 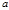 по модулю
по модулю  при основании
при основании  и обозначается
и обозначается 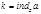 )))
)))
Если величина основания 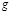 не важна, то можно обозначать
не важна, то можно обозначать 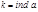 Таким образом, из (7) имеем
Таким образом, из (7) имеем
 . (8)
. (8)
Свойства индексов.
1. 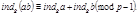 Пусть
Пусть 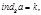 тогда
тогда 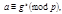
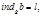 тогда Перемножая сравнения, получаем:
тогда Перемножая сравнения, получаем: 
Так как 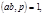 то
то 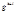 сравнимо с одним из чисел ряда
сравнимо с одним из чисел ряда  Разделим
Разделим 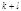 на
на 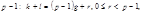 т.е.
т.е.  . (9)
. (9)
Тогда 
 Отсюда
Отсюда  Подставляем в равенство (9) значения
Подставляем в равенство (9) значения 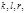 получаем
получаем 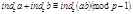
2. 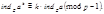
3. 
4.  первообразный корень.
первообразный корень.
5. 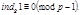
6. Если  первообразный корень, то
первообразный корень, то 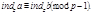
Для примера докажем свойство 1
Доказательство.
Пусть 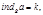 тогда
тогда 
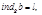 тогда
тогда 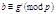 Перемножая сравнения, получаем:
Перемножая сравнения, получаем: 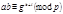
Так как 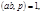 то
то 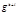 сравнимо с одним из чисел ряда
сравнимо с одним из чисел ряда 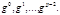 Разделим
Разделим  на
на 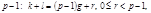 т.е.
т.е.  . (9)
. (9)
Тогда 
 Отсюда
Отсюда  Подставляем в равенство (9) значения
Подставляем в равенство (9) значения 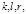 получаем
получаем 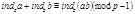
Замечание. По простому модулю  для каждого числа существует бесконечное множество индексов, сравнимых по модулю
для каждого числа существует бесконечное множество индексов, сравнимых по модулю 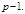 Обычно из всех возможных значений индекса по данному основанию берут наименьшее. Индексы имеют большие приложения. Для удобства составляют таблицы индексов. Для составления таблицы индексов по модулю
Обычно из всех возможных значений индекса по данному основанию берут наименьшее. Индексы имеют большие приложения. Для удобства составляют таблицы индексов. Для составления таблицы индексов по модулю 
1) находим первообразный корень  по модулю
по модулю 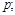
2) вычисляем все степени 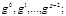
3) составляем таблицу.
Замечание1. По таблице можно определить, для какого первообразного корня она составлена.
Замечание2. Для удобства составляют также таблицу антииндексов, определяющую по индексу I число.
Замечание3. Таблицы индексов для простых модулей p содержат индексы чисел от 1 до p-1. Для каждого такого числа и всех сравнимых с ним по модулю p в таблице указывается индекс, представляющий собой одно из чисел 0,1,…,р-2. В некоторых таблицах в качестве индекса единицы указывается не 0, а р-1.
Замечание4. Для составных модулей 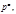
 (p- простое нечётное число) существуют первообразные корни, и поэтому для любого числа, взаимно простого с таким модулем, существуют индексы.
(p- простое нечётное число) существуют первообразные корни, и поэтому для любого числа, взаимно простого с таким модулем, существуют индексы.

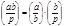
 .
.
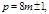 то
то  .Если
.Если 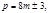 то
то  Поэтому
Поэтому 
 и
и 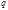 нечётные простые числа, то, или
нечётные простые числа, то, или 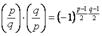 Или
Или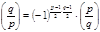 . (11)
. (11)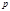 или
или 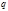 имеет форму
имеет форму  , то показатель в правой части (11) чётный, и
, то показатель в правой части (11) чётный, и  . Если и
. Если и  или
или  имеет форму
имеет форму 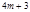 , то показатель в правой части (11) нечётный, и
, то показатель в правой части (11) нечётный, и 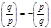 .
.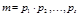 , где
, где 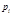 - простые числа, среди которых могут быть одинаковые,
- простые числа, среди которых могут быть одинаковые, 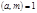 .Символ Якоби определяется равенством
.Символ Якоби определяется равенством  , (12)
, (12)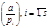 - символы Лежандра.Читается
- символы Лежандра.Читается 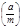 - «символ Якоби
- «символ Якоби  по отношению к
по отношению к 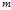 ».
». 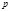 , а о нечётных числах
, а о нечётных числах  .Из замечаний следует, что при вычислении символа Лежандра удобно рассматривать его как символ Якоби, тогда отпадает необходимость выделять из числителя его нечётные простые множители.По значению символа Якоби можно сказать следующее:
.Из замечаний следует, что при вычислении символа Лежандра удобно рассматривать его как символ Якоби, тогда отпадает необходимость выделять из числителя его нечётные простые множители.По значению символа Якоби можно сказать следующее: , то
, то  - квадратичный невычет по
- квадратичный невычет по 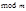 ;- если
;- если 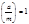 и
и 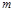 - нечётное составное число, то о квадратичности вычета
- нечётное составное число, то о квадратичности вычета  по
по 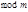 ничего сказать нельзя.
ничего сказать нельзя.  то
то  .
.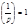 , т.е. 1 – квадратичный вычет для любого нечётного простого
, т.е. 1 – квадратичный вычет для любого нечётного простого  всегда разрешимо.
всегда разрешимо.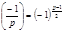
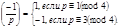
 .
.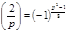

 42 Сравнения второй степени по составному модулю
42 Сравнения второй степени по составному модулю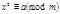 . (13)
. (13) , где
, где 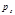 - различные нечётные простые числа,
- различные нечётные простые числа,  2. если
2. если 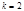 , то
, то 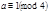 , а если
, а если 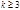 , то
, то 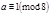 .
.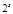 при
при 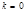 и
и 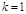 ;
;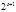 при
при 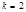 ;
;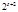 при
при 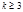 .
. 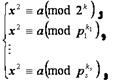 (14)
(14)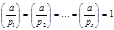 , то
, то и
и  первое сравнение (14) имеет одно решение, каждое последующее сравнение имеет по два решения. Тогда система (14) и сравнение (13) имеет
первое сравнение (14) имеет одно решение, каждое последующее сравнение имеет по два решения. Тогда система (14) и сравнение (13) имеет 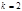 и
и 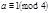 каждое сравнение в (14) имеет по два решения. Тогда система (14) и сравнение (13) имеет
каждое сравнение в (14) имеет по два решения. Тогда система (14) и сравнение (13) имеет 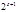 решений;
решений;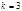 ,
, 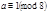 первое сравнение имеет
первое сравнение имеет  решения (доказать самостоятельно). Тогда система (14) и сравнение (13) имеет
решения (доказать самостоятельно). Тогда система (14) и сравнение (13) имеет 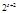 решений.
решений.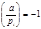 ;
;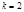
 ;
;
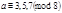 ;
;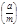 . Однако, если
. Однако, если 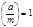 ничего о числе решений мы сказать не можем.
ничего о числе решений мы сказать не можем.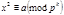 (где
(где 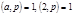 ) имеет два решения, если
) имеет два решения, если  и не имеет решений, если
и не имеет решений, если 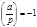 . (без доказательства).
. (без доказательства).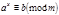 называется показательным. Изучение таких сравнений сводится к изучению сравнений вид
называется показательным. Изучение таких сравнений сводится к изучению сравнений вид  . (1)
. (1)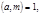 то по теореме Эйлера
то по теореме Эйлера  следовательно сравнение (1) при
следовательно сравнение (1) при 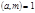 всегда имеет решение.
всегда имеет решение.  сравнения (1) называется показателем числа
сравнения (1) называется показателем числа  принадлежит показателю
принадлежит показателю 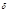 по модулю
по модулю  Записывают
Записывают  .
. 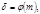 называются первообразными корнями по модулю
называются первообразными корнями по модулю 
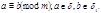 Т.к.
Т.к. 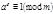 и
и 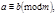 то
то  следовательно
следовательно  Т.к.
Т.к.  и
и 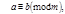 то
то 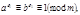 следовательно
следовательно  Отсюда
Отсюда 
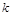 является решением сравнения (1) и
является решением сравнения (1) и  то
то 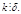
 и
и  Т.к.
Т.к.  решение сравнения (1), то
решение сравнения (1), то 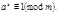 Тогда
Тогда 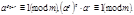
 то
то  поэтому
поэтому 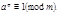 Но,
Но, 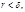 следовательно
следовательно  Таким образом,
Таким образом,  т. е.
т. е. 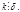
 то
то 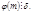
 т.е.
т.е.  решение сравнения (1). Следовательно,
решение сравнения (1). Следовательно, 
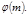
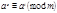 имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда  где
где 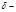 показатель числа
показатель числа  по модулю
по модулю 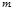
 и для определённости
и для определённости 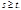 Т.к.
Т.к.  то
то 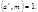 Сократим сравнение на
Сократим сравнение на 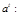
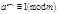 Тогда по свойству
Тогда по свойству 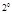
 следовательно,
следовательно, 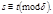
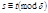 и
и  Тогда
Тогда 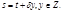 Получаем
Получаем 
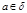 по модулю
по модулю 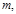 то числа
то числа 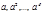 попарно не сравнимы по модулю
попарно не сравнимы по модулю 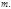

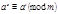 тогда и только тогда, когда
тогда и только тогда, когда 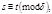 но среди показателей последовательности (2) нет сравнимых по модулю
но среди показателей последовательности (2) нет сравнимых по модулю 
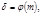 называются первообразными корнями по модулю
называются первообразными корнями по модулю 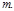
 числа
числа  либо не является показателем какого-либо класса вычетов, либо является для
либо не является показателем какого-либо класса вычетов, либо является для 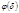 таких классов ( доказательство самостоятельно).
таких классов ( доказательство самостоятельно). 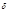 числа
числа 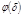 классов.
классов. 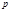 существует
существует  классов первообразных корней.
классов первообразных корней. 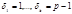 все делители числа
все делители числа 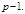 Распределяя вычеты приведённой системы вычетов по модулю
Распределяя вычеты приведённой системы вычетов по модулю 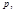 т.е. числа
т.е. числа 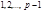 в отдельные группы по принадлежности своему показателю, всего должны получить
в отдельные группы по принадлежности своему показателю, всего должны получить 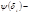 число чисел приведённой системы, принадлежащих показателю
число чисел приведённой системы, принадлежащих показателю 
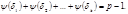 (3)
(3) 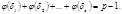 (4) Приравнивая (3) и (4), получаем
(4) Приравнивая (3) и (4), получаем 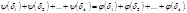 Согласно лемме
Согласно лемме 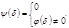 Отсюда в равенстве (5) всегда
Отсюда в равенстве (5) всегда 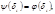 т.к. если хотя бы одно
т.к. если хотя бы одно  то в правой части (5) останется лишний положительный член и равенство нарушается. Тогда получаем, что для делителя
то в правой части (5) останется лишний положительный член и равенство нарушается. Тогда получаем, что для делителя  существует
существует 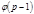 классов первообразных корней.
классов первообразных корней. 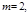

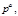
 где
где 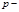 простое нечётное число,
простое нечётное число, 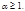
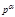 и
и 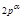 . Теорема об отыскании первообразных корней
. Теорема об отыскании первообразных корней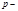 простое нечётное число и
простое нечётное число и 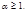 Первообразные корни по модулям
Первообразные корни по модулям 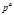 и
и 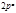 связаны следующим свойством:
связаны следующим свойством: 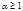 и
и 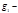 первообразный корень по модулю
первообразный корень по модулю 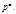 Нечётное из чисел
Нечётное из чисел 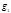 и
и 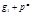 будет первообразным корнем по модулю
будет первообразным корнем по модулю  Первообразные корни по модулям
Первообразные корни по модулям 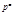 и
и 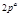 можно находить, пользуясь теоремой:
можно находить, пользуясь теоремой: 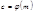 и
и 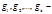 различные простые делители числа
различные простые делители числа  Для того, чтобы число
Для того, чтобы число 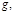 взаимно простое с модулем
взаимно простое с модулем 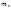 было первообразным корнем по модулю
было первообразным корнем по модулю 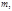 необходимо и достаточно, чтобы это
необходимо и достаточно, чтобы это 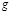 не удовлетворяло ни одному из сравнений
не удовлетворяло ни одному из сравнений 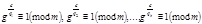 .
.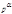 и
и  первообразный корень по простому модулю
первообразный корень по простому модулю  тогда числа
тогда числа  представляют собой приведённую систему вычетов по модулю
представляют собой приведённую систему вычетов по модулю 
 взаимно простого с
взаимно простого с  найдётся единственное число
найдётся единственное число 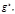 принадлежащее тому же классу по модулю
принадлежащее тому же классу по модулю 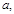 т.е.
т.е.  где
где 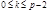 . Это позволяет ввести понятие индекса.
. Это позволяет ввести понятие индекса. 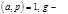 первообразный корень по модулю
первообразный корень по модулю  Если выполняется сравнение (7), то число
Если выполняется сравнение (7), то число  называется индексом числа
называется индексом числа 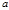 по модулю
по модулю  и обозначается
и обозначается 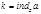 )))
))) 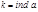 Таким образом, из (7) имеем
Таким образом, из (7) имеем . (8)
. (8) 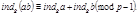 Пусть
Пусть 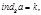 тогда
тогда 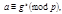
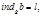 тогда Перемножая сравнения, получаем:
тогда Перемножая сравнения, получаем: 
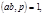 то
то 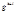 сравнимо с одним из чисел ряда
сравнимо с одним из чисел ряда  Разделим
Разделим 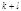 на
на 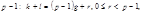 т.е.
т.е.  . (9)
. (9)
 Отсюда
Отсюда  Подставляем в равенство (9) значения
Подставляем в равенство (9) значения 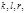 получаем
получаем 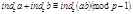
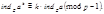

 первообразный корень.
первообразный корень.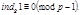
 первообразный корень, то
первообразный корень, то 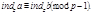
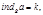 тогда
тогда 
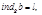 тогда
тогда 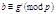 Перемножая сравнения, получаем:
Перемножая сравнения, получаем: 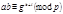
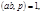 то
то 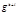 сравнимо с одним из чисел ряда
сравнимо с одним из чисел ряда 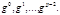 Разделим
Разделим  на
на 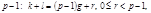 т.е.
т.е.  . (9)
. (9) Отсюда
Отсюда 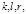 получаем
получаем 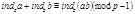

 по модулю
по модулю 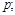
 (p- простое нечётное число) существуют первообразные корни, и поэтому для любого числа, взаимно простого с таким модулем, существуют индексы.
(p- простое нечётное число) существуют первообразные корни, и поэтому для любого числа, взаимно простого с таким модулем, существуют индексы.


