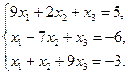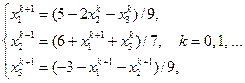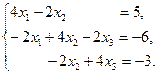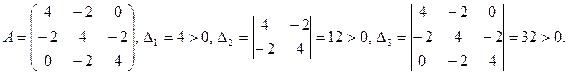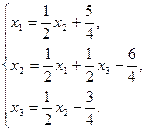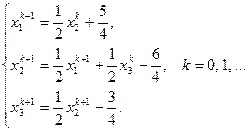Метод Зейделя. Пусть требуется решить систему уравнений (3.1):Пусть требуется решить систему уравнений (3.1):
Выразим из первого уравнения переменную x 1, из второго — x 2, и т.д.:
Пусть k -е приближение к решению обозначено так Расчетные формулы метода Зейделя можно записать в виде:
Теорема 3.3 (достаточные условия сходимости [1]). Пусть при всех i для коэффициентов системы уравнений (3.25) выполняются условия
Тогда метод Зейделя сходится и выполняется неравенство
где x * — точное решение системы (3.25). Если матрица A удовлетворяет условию (3.27), то говорят, что A — матрица с диагональным преобладанием. Пример 3.5. Решить систему уравнений методом итераций и методом Зейделя. Сравнить скорости сходимости методов.
Решение. Очевидно, матрица коэффициентов системы уравнений имеет диагональное преобладание. Выразим из каждого уравнения соответствующую переменную
и запишем расчетные формулы метода Зейделя
Введем в программе Excel обозначения в ячейках A 1: D 1, начальные значения в ячейках B 2: D 2 и формулы в ячейках B 3: D 3, как показано в таблице 3.4. Выделим диапазон B 3: D 3 и протянем маркер заполнения вниз до ячейки D 12. Для нумерации последовательных приближений выделим диапазон A 2: A 3 и протянем маркер заполнения вниз до ячейки A 12. Получим 10 последовательных приближений к решению. Таблица 3.4
Результаты расчетов приведены в таблице 3.5. Как видим, есть сходимость процесса итераций, так как соответствующие компоненты векторов x 9 и x 10 содержат по 8 одинаковых значащих цифр, начиная слева направо. Норма разности || x 10 – x 9||1 = 3,92663E–10 < 0,000000001. Таблица 3.5
Приведем результаты решения системы методом итераций. Если в таблице 3.4 формулы в третьей строке заменить на формулы метода итераций, как показано в ячейках A 3: D 3 таблицы 3.6, затем выделить A 3: D 3 и скопировать вниз маркером заполнения до строки 12, то получим таблицу 3.7. Таблица 3.6
Сравнивая таблицы 3.5 и 3.7, мы видим, что метод Зейделя имеет более высокую скорость сходимости, чем метод итераций. Например, на шаге k = 4, метод итераций дает погрешность 0,012514, а метод Зейделя имеет на этом же шаге погрешность 0,000878056. Таблица 3.7
Теорема 3.4 (достаточные условия сходимости [1]).Пусть матрица A системы (3.1) — вещественная, симметричная и положительно определенная. Тогда метод Зейделя сходится. Пример 3.6. Решить методом Зейделя систему уравнений
Решение. Матрица системы симметрична, но не имеет диагонального преобладания.Применяя критерий Сильвестра (см. ниже п. 3.6, теорема 3.8), покажем, что матрица системы положительно определена:
Согласно теореме 3.4 метод Зейделя для данной системы сходится. Выразим из каждого уравнения соответствующую переменную и запишем формулы метода Зейделя:
Аналогично примеру 3.5 по данным расчетным формулам можно вычислить решение системы линейных уравнений. Составим программу на языке C ++ для решения системы уравнений методом Зейделя (3.26):
#include <except.h> #include <iostream.h> #include <math.h> int Zeidel(long double **a, long double *b, long double *x, long double eps, int k_max, const int n); int main(){ long double **a; long double *b, *x, eps; int i,j,n,k_max; cout <<"\n input n = "; cin >> n; cout <<"\n input eps = "; cin >> eps; cout <<"\n input k_max = "; cin >> k_max; try { a= new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n]; b= new long double[n]; x= new long double[n]; } catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);} cout <<"\n input matrix a \n"; for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j]; cout <<"\n input vector b\n"; for (i=0; i<n; i++)cin >> b[i]; cout << "\n matrix a: "; for (i=0; i<n; i++){cout << "\n"; for (j=0; j<n; j++) cout <<" "<< a[i][j];} cout << "\n vector b: "; for (i=0; i<n; i++)cout << "\n " << b[i]; Zeidel(a, b, x,eps,k_max, n); cout << "\n vector x: "; for (i=0; i<n; i++)cout << "\n x[" << i <<"] = " << x[i]; cout << "\n Press Key and Enter to continue"; cin >> i; // for pause for(i=0;i<n;i++)delete[] a[i]; delete a; delete[] b; delete[] x; return 0; }//end main int Zeidel(long double **a, long double *b, long double *x, long double eps, int k_max, const int n){ int i, j, m; long double *x1, xerr, s; try {x1 = new long double[n];} catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);} for (i = 0; i < n; i++)x1[i] = x[i]; for (m = 0; m <= k_max; m++) {// m for (i = 0; i < n; i++){ //i s = b[i]; for (j = 0; j < n; j++) if(j!= i)s = s - a[i][j]*x1[j]; x1[i] = s / a[i][i];}//end i xerr = 0; for (i = 0; i < n; i++) xerr = xerr + (x1[i] - x[i])* (x1[i] - x[i]); xerr = sqrt(xerr); for (i = 0; i < n; i++)x[i] = x1[i]; if(xerr < eps) break; }// end m delete[] x1; return 0; }// end iter
Найдем с помощью этой программы решение системы уравнений примера 3.4:
input n = 3 input eps = 0.0000001 input k_max = 10000 input matrix a 4 –2 0 –2 4 –2 0 –2 4 Input vector c 5 –6 –3 matrix a: 4 –2 0 –2 4 –2 0 –2 4 vector 5: –6 –3 vector x: x[0] = 4.84288e–08 x[1] = –2.5 x[2] = –2 Press Key and Enter to continue
Ответ: x = (0; –2,5; –2).
|

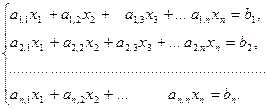 (3.25)
(3.25)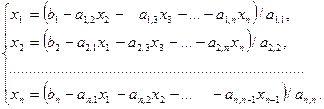
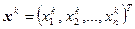 . Подставим его в правую часть полученной системы и выразим следующее приближение
. Подставим его в правую часть полученной системы и выразим следующее приближение 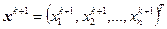 . В отличие от метода итераций, метод Зейделя использует при вычислении
. В отличие от метода итераций, метод Зейделя использует при вычислении 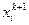 уже найденные компоненты
уже найденные компоненты 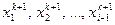 вектора x k +1.
вектора x k +1.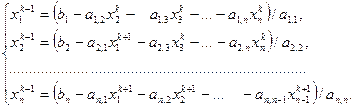 (3.26)
(3.26)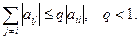 (3.27)
(3.27)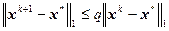 , (3.28)
, (3.28)