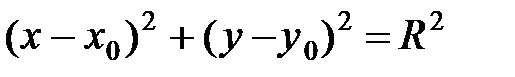Приведение общего уравнения линии второго порядка к каноническому видуДля исследований приведем общее уравнение линии второго порядка к одному из канонических видов. Существует такая система координат, в которой уравнение (1) не содержит произведения xy, то есть B = 0. Пусть Чертеж 1. Найдем связь между этими координатами. Очевидно, что:
Рассмотрим Рассмотрим теперь Таким образом, с учетом того, что Следовательно, система (6) представляет собой выражение старых координат Замечание. Для того чтобы получить выражение новых координат через старые, достаточно угол α в формулах (6) заменить на угол (−α), так как при повороте системы координат X′OY ′ на угол (−α) мы получим систему XOY. Подставим формулы (6) в уравнение (1), получим:
При
При
При
При
При
Таким образом, уравнение (1) с учётом замены (6) принимает вид:
Подберем угол После данного преобразования уравнение (1) примет вид:
Докажем, что при повороте на любой угол α имеет место равенство:
Так как мы подобрали угол α так, что
Чтобы проанализировать уравнение кривой (9), рассмотрим три случая: 1) 2) 3) Подробнее рассмотрим эллиптический случай. Из
Дополним члены, содержащие x’ и y’,до полного квадрата:
где Положим a) Пусть
Так как Из (14) и (15) следует, что мы получили каноническое уравнение эллипса b) Пусть F′ > 0, тогда в уравнении (13) слева стоит неотрицательное число, а справа - отрицательное, поэтому точек, удовлетворяющих данному уравнению, не существует. c) Пусть F′ = 0. Тогда уравнению (13) удовлетворяет только одна точка Рассмотрим гиперболический случай. Из a) Предположим, что
Так как тогда мы получаем каноническое уравнение гиперболы:
b) При Пусть Рассмотрим параболический случай. Так как a) Пусть Соберём члены, содержащие
где Рассмотрим два случая: · Пусть где Положим Это каноническое уравнение параболы, симметричной относительно оси (OY). · Пусть
1. Если 2. Если b) Пусть
Если
Вывод. Путем преобразований кривой второго порядка, определяемой уравнением (1) мы можем получить уравнения таких линии второго порядка, как: 1. 2. 3. 4. 5.
Содержание темы «Линии второго порядка» в элементарной математике В математике рассматриваются линии второго порядка, как конические сечения: окружность, эллипс, гипербола, парабола; или как множество точек обладающих некоторыми свойствами. Рассмотрим каждую линию второго порядка подробнее, определяя линии как множество точек. ОКРУЖНОСТЬ Определение 1.1. Окружность - множество точек плоскости, равноудаленных от данной точки М0, называемой ее центром.[9.С.65] Общий вид уравнения
|

 координаты точки M в системе координат XOY. Повернем оси координат на угол
координаты точки M в системе координат XOY. Повернем оси координат на угол 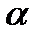 в положительном направлении и обозначим (x', y') координаты точки M в новой системе координат X'OY'. (чертеж 1.)
в положительном направлении и обозначим (x', y') координаты точки M в новой системе координат X'OY'. (чертеж 1.) (так как
(так как  ); (2)
); (2) (так как
(так как  ); (3)
); (3)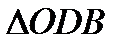 . Так как он прямоугольный, то
. Так как он прямоугольный, то  ,
,  . (4)
. (4) . Он также прямоугольный, поэтому
. Он также прямоугольный, поэтому  ,
, 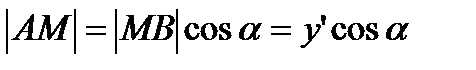 . (5)
. (5) , из равенств (2)-(5) получим:
, из равенств (2)-(5) получим:  (6)
(6)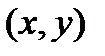 через новые
через новые 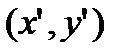 при повороте XOY на угол α вокруг О (0,0).
при повороте XOY на угол α вокруг О (0,0). Соберем коэффициенты при соответствующих неизвестных.
Соберем коэффициенты при соответствующих неизвестных.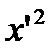 , получим:
, получим: ,
, :
: , (7)
, (7) :
: ,
, :
: ,
, :
: .
.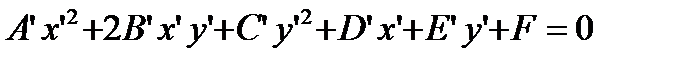 (8)
(8) таким образом, чтобы коэффициент
таким образом, чтобы коэффициент  . Из (7) следует, что
. Из (7) следует, что  поэтому
поэтому 
 . (9)
. (9) (10)
(10) , то из (10) следует, что
, то из (10) следует, что . (11)
. (11) (эллиптический случай);
(эллиптический случай); (гиперболический случай);
(гиперболический случай); (параболический случай).
(параболический случай). , то есть знаки
, то есть знаки  совпадают. Пусть A′ > 0, C′ > 0. Выделим полные квадраты при неизвестных x′, y′, получим:
совпадают. Пусть A′ > 0, C′ > 0. Выделим полные квадраты при неизвестных x′, y′, получим:
 , (12)
, (12)
 , тогда уравнение (12) примет вид:
, тогда уравнение (12) примет вид:  . (13)
. (13) . Разделим обе части уравнения (13) на
. Разделим обе части уравнения (13) на  , получим:
, получим: (14)
(14) и
и  , то предположим, что
, то предположим, что 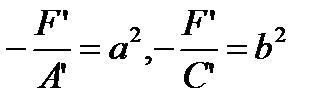 . (15)
. (15)
 , то есть точка с координатами
, то есть точка с координатами 
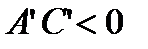 , то есть числа
, то есть числа  имеют разные знаки. Выполняя аналогичные преобразования, как и для эллиптического случая, получим уравнение кривой:
имеют разные знаки. Выполняя аналогичные преобразования, как и для эллиптического случая, получим уравнение кривой: 
 . Отсюда:
. Отсюда: (16)
(16) и
и  разных знаков, следовательно, одна из скобок больше нуля, другая скобка меньше нуля. Пусть
разных знаков, следовательно, одна из скобок больше нуля, другая скобка меньше нуля. Пусть  (17)
(17)
 уравнение принимает вид:
уравнение принимает вид:  (18)
(18) , тогда
, тогда  и уравнение (18) примет вид:
и уравнение (18) примет вид:  откуда
откуда  Таким образом, получили уравнения двух пересекающихся прямых.
Таким образом, получили уравнения двух пересекающихся прямых.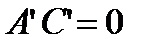 .
. . Так как после поворота
. Так как после поворота  , то уравнение (9) преобразуется до вида:
, то уравнение (9) преобразуется до вида:  (19)
(19) , и дополним их до полного квадрата:
, и дополним их до полного квадрата: тогда уравнение (19) примет вид:
тогда уравнение (19) примет вид:  или
или  , (20)
, (20) . Из (20) следует, что
. Из (20) следует, что 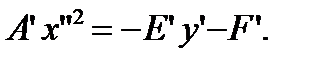
 , тогда
, тогда  , то есть
, то есть 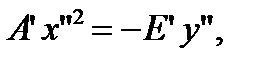 (21)
(21)
 , тогда уравнение (21) примет вид:
, тогда уравнение (21) примет вид: 
 , тогда уравнение (20) перепишется в виде
, тогда уравнение (20) перепишется в виде (22)
(22) , то получим уравнение оси (OY)
, то получим уравнение оси (OY)  .
. , то возможны два случая. Если A′ и F′ одного знака, то точек, удовлетворяющих данному уравнению, нет; если же A′ и F′ разных знаков, то
, то возможны два случая. Если A′ и F′ одного знака, то точек, удовлетворяющих данному уравнению, нет; если же A′ и F′ разных знаков, то 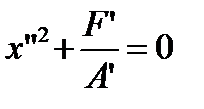 , где
, где  , поэтому
, поэтому  и уравнение (22) описывает две параллельные прямые:
и уравнение (22) описывает две параллельные прямые: 
 , тогда уравнение (9) примет вид
, тогда уравнение (9) примет вид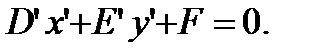 (23)
(23)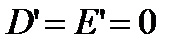 , а
, а  , то точек, удовлетворяющих уравнению (23), нет; если же
, то точек, удовлетворяющих уравнению (23), нет; если же  или
или  отличны от нуля, то уравнение (23) описывает прямую.
отличны от нуля, то уравнение (23) описывает прямую. - уравнение эллипса
- уравнение эллипса - уравнение гиперболы
- уравнение гиперболы - уравнение параболы
- уравнение параболы - совокупности двуз пересекающихся прямых
- совокупности двуз пересекающихся прямых - совокупности двух параллельных прямых
- совокупности двух параллельных прямых