Исследование свойств гиперболы по ее уравнению1) Пересечение гиперболы с осями координат:
Очевидно, что гипербола состоит из двух ветвей: правой и левой, простирающихся в бесконечность. В уравнении (12) положим, что y=0, получим:
Чертеж 19. Положим, что в уравнении (12) х=0, и получим: ЗАМЕЧАНИЕ: Если мнимая ось гиперболы имеет длину 2a и направлена по оси (OX), а действительная ось длиной 2b совпадает с осью (OY), то уравнение гиперболы имеет вид: Определение 3.2. Гиперболы, заданные уравнениями Определение 3.3. Если a=b, гипербола называется равносторонней. 2) Симметрии гиперболы относительно координатных осей Пусть
Точка Точка 3) Асимптоты гиперболы: Текущая точка гиперболы при движении по ней в бесконечность неограниченно приближается к некоторой прямой, которая называется асимптотой гиперболы. Асимптотами являются прямые, которые имеют следующие уравнения:
Пусть текущая точка гиперболы, Доказательство:
Умножим и разделим равенство (13) на (
При
Чертеж 20.
4) Фокусы гиперболы: Пусть фокусы гиперболы лежат на оси Ох. Межфокусное расстояние гиперболы равно
Следовательно, 5) Директориальное свойство гиперболы: Определение 3.4. Директрисами гиперболы называются прямые, параллельные канонической оси ОУ и отстоящие от этой оси на расстояние Уравнения директрис гиперболы имеют вид: ++
6) Эксцентриситет гиперболы: Определение 3.5. Отношение Если при постоянном значении
Чертеж 21. Если
Чертеж 22. 7) Касательная к гиперболе: Уравнение касательной к гиперболе
Чертеж 23. 8) Диаметр гиперболы: Если гипербола задана уравнением
ПАРАБОЛА Определение 4.1. Парабола- это геометрическое множество точек, для каждой из которых расстояние от некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой (директриса не проходит через фокус). [8.С.589] Общий вид уравнения
|

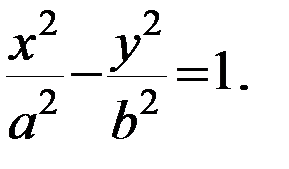

 отсюда
отсюда  . Следовательно, точки
. Следовательно, точки  являются точками пересечения гиперболы с осью
являются точками пересечения гиперболы с осью  (чертеж 19.).
(чертеж 19.).

 , следовательно, уравнение гиперболы не пересекает ось
, следовательно, уравнение гиперболы не пересекает ось  .
. . [1.С.107-108]
. [1.С.107-108] и
и  принадлежит гиперболе, то есть
принадлежит гиперболе, то есть  верное равенство. Точка
верное равенство. Точка  симметрична точке
симметрична точке  относительно оси ОХ:
относительно оси ОХ:
 - верное равенство. Следовательно,
- верное равенство. Следовательно, 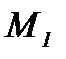 принадлежит гиперболе, следовательно, гипербола симметрична относительно ОХ.
принадлежит гиперболе, следовательно, гипербола симметрична относительно ОХ. симметрична точке
симметрична точке  симметрична точке
симметрична точке  и
и  ,
, ее проекция на ось абсцисс. Прямая
ее проекция на ось абсцисс. Прямая  пересекает прямую
пересекает прямую  , заданную указанным уравнением в точке
, заданную указанным уравнением в точке  . Докажем: что
. Докажем: что  при
при  .
. .Расстояние
.Расстояние  это ордината точки
это ордината точки  , лежащей на прямой
, лежащей на прямой  это ордината точки
это ордината точки  гиперболы, которую находим из её канонического уравнения:
гиперболы, которую находим из её канонического уравнения:  Тогда
Тогда 

 ),следовательно, получим:
),следовательно, получим:
 знаменатель дроби неограниченно увеличивается, следовательно, дробь стремится к нулю.
знаменатель дроби неограниченно увеличивается, следовательно, дробь стремится к нулю. - уравнение гиперболы, в которой
- уравнение гиперболы, в которой  а
а  - являются асимптотами гиперболы. (чертеж 20.) [1.С.108]
- являются асимптотами гиперболы. (чертеж 20.) [1.С.108]
 причем
причем  . Заметим, что
. Заметим, что  по определению гиперболы.
по определению гиперболы.


 фокусы гиперболы. [1.С.109]
фокусы гиперболы. [1.С.109] .
. и
и  , если гипербола задана уравнением
, если гипербола задана уравнением  . Если гипербола задана уравнением
. Если гипербола задана уравнением  , то директрисы определяются уравнениями
, то директрисы определяются уравнениями  .
. называется эксцентриситетом гиперболы. Так как
называется эксцентриситетом гиперболы. Так как  , то
, то 
 , число
, число  будет изменяться от нуля до бесконечности, то
будет изменяться от нуля до бесконечности, то 
 будет измениться от
будет измениться от  , то гипербола будет стремиться к лучам (чертеж 21.).
, то гипербола будет стремиться к лучам (чертеж 21.).
 , то гипербола будет стремиться к параллельным прямым (чертеж 22.). [1.С.109]
, то гипербола будет стремиться к параллельным прямым (чертеж 22.). [1.С.109]
 , где
, где  - координаты точки касания, а
- координаты точки касания, а  соответственно действительная и мнимая полуоси гиперболы (чертеж 23.).
соответственно действительная и мнимая полуоси гиперболы (чертеж 23.).
 , то её диамерт, сопряженный хордам с угловым коэффициентом k, определяется уравнением
, то её диамерт, сопряженный хордам с угловым коэффициентом k, определяется уравнением  .
. .
.


