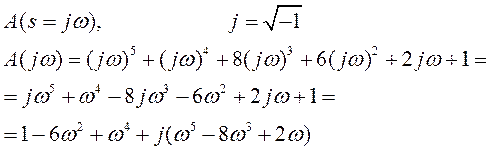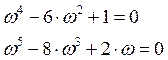Частотный критерий устойчивости МихайловаЧастотный критерий устойчивости Михайлова основан на построении годографа A (jw)
Представляя его в виде суммы вещественной и мнимой составляющих, имеем
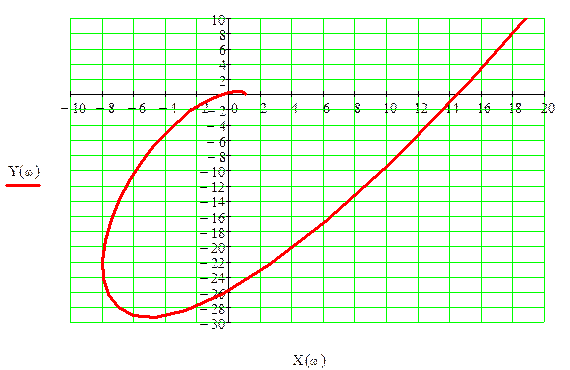
Задаваясь значением начиная с точки Критерий устойчивости Михайлова формулируется следующим образом: система автоматического управления устойчива, если годограф Михайлова, начинаясь при w =0 на вещественной положительной полуоси, последовательно обходит n квадрантов координатной плоскости против часовой стрелки, где n - порядок системы.
Построим годограф Михайлова для системы с передаточной функцией
Производится замена оператора Лапласа s на комплексную переменную j× w и группируются слагаемые по степеням w.
Составляющие вектора A (jw)= X (w)+ j × Y (w) имеют вид
Найти частоты, соответствующие пересечениям годографа с осями координат. Для этого необходимо найти решения отдельных уравнений:
Результаты расчета приведены в таблице ниже. Таблица
Из таблицы следует, что годограф последовательно обходит пять квадрантов, поэтому исследуемая система устойчива.
Рис. Годограф Михайлова Построение весовой функции w (t) тоже свидетельствует об устойчивости исследуемой системы, весовая функция w (t) стремится к 0.
Рис. График весовой функции w (t)
|
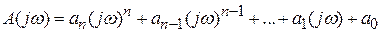
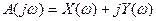
=0, вычисляем и откладываем значения 
и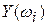 
. Совокупность этих точек, соединенная плавной кривой, образует годограф Михайлова (рис.).
.
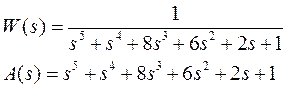