Неотрицательная случайная величина 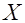 имеет гамма-распределение, если ее плотность распределения выражается формулой
имеет гамма-распределение, если ее плотность распределения выражается формулой
 ,
,  , (5)
, (5)
где  и
и  ,
,  – гамма-функция:
– гамма-функция:
 . (6)
. (6)
Таким образом, гамма-распределение является двухпараметрическим распределением, оно занимает важное место в математической статистике и теории надежности. Это распределение имеет ограничение с одной стороны 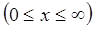 .
.
Если параметр формы кривой распределения  – целое число, то гамма-распределение описывает время, необходимое для появления
– целое число, то гамма-распределение описывает время, необходимое для появления  событий (отказов), при условии, что они независимы и появляются с постоянной интенсивностью
событий (отказов), при условии, что они независимы и появляются с постоянной интенсивностью  .
.
В большинстве случаев это распределение описывает наработку системы с резервированием отказов стареющих элементов, время восстановления системы с резервированием отказов стареющих элементов, время восстановления системы и т. д. При различных количественных значениях параметров гамма-распределение принимает самые разнообразные формы, что и объясняет его широкое применение.
Плотность вероятности гамма-распределения определяется равенством, если
 и
и 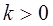 :
:  , (7)
, (7)
где  . (8)
. (8)
Функция распределения  . (9)
. (9)
Заметим, что функция надежности выражается формулой:
 . (10)
. (10)
Гамма-функция обладает свойствами:  ,
,  , (11)
, (11)
откуда следует, что если 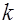 – целое неотрицательное число, то
– целое неотрицательное число, то
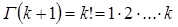 . (12)
. (12)
Кроме того, нам в последующем потребуется еще одно свойство гамма-функции:  ;
;  . (13)
. (13)
Пример. Восстановление радиоэлектронной аппаратуры подчиняется закону гамма-распределения с параметрами  и
и  . Определить вероятность восстановления аппаратуры за
. Определить вероятность восстановления аппаратуры за 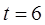 час.
час.
Решение. Для определения вероятности восстановления воспользуемся формулой (9)  .
.
Для целых положительных значений  функции
функции  , а при
, а при 
 .
.
Если перейти к новым переменным, значения которых будут выражены  ;
;  , то получим табличный интеграл:
, то получим табличный интеграл:
 .
.
В этом выражении решение интеграла в правой части можно определить по той же формуле:
 ,
,
а при  будет
будет
 .
.
При  и
и  новые переменные будут равны
новые переменные будут равны  и
и  , а сам интеграл будет равен
, а сам интеграл будет равен
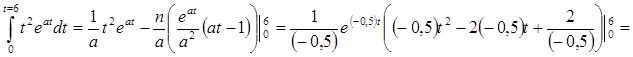
 .
.
Значение функции  будет равно
будет равно
 .
.
Ответ: 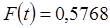 .
.
Найдем числовые характеристики случайной величины  , подчиненной гамма-распределению
, подчиненной гамма-распределению
 .
.
В соответствии с равенством (13) получим  . (14)
. (14)
Второй начальный момент найдем по формуле
 ,
,
откуда  . (15)
. (15)
Заметим, что при 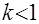 интенсивность отказов монотонно убывает, что соответствует периоду приработки изделия. При
интенсивность отказов монотонно убывает, что соответствует периоду приработки изделия. При 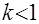 интенсивность отказов возрастает, что характеризует период изнашивания и старения элементов.
интенсивность отказов возрастает, что характеризует период изнашивания и старения элементов.
При  гамма-распределение совпадает с экспоненциальным распределением, при
гамма-распределение совпадает с экспоненциальным распределением, при  гамма-распределение приближается к нормальному закону. Если
гамма-распределение приближается к нормальному закону. Если 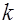 принимает значения произвольных целых положительных чисел, то такое гамма-распределение называют распределением Эрланга
принимает значения произвольных целых положительных чисел, то такое гамма-распределение называют распределением Эрланга  -го порядка:
-го порядка:
 ,
, 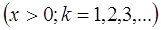 . (16)
. (16)
Здесь достаточно лишь указать, что закону Эрланга 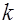 -го порядка подчинена сумма независимых случайных величин
-го порядка подчинена сумма независимых случайных величин  , каждая из которых распределена по показательному закону с параметром
, каждая из которых распределена по показательному закону с параметром  . Закон Эрланга
. Закон Эрланга 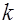 -го порядка тесно связан со стационарным пуассоновским (простейшим) потоком с интенсивностью
-го порядка тесно связан со стационарным пуассоновским (простейшим) потоком с интенсивностью  .
.
Действительно, пусть имеется такой поток событий во времени (рис. 6).
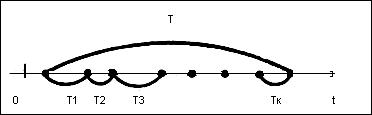
Рис. 6. Графическое представление пуассоновского потока событий во времени
Рассмотрим интервал времени  , состоящий из суммы
, состоящий из суммы 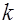 интервалов между событиями в таком потоке. Можно доказать, что случайная величина
интервалов между событиями в таком потоке. Можно доказать, что случайная величина  будет подчинена закону Эрланга
будет подчинена закону Эрланга 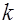 -го порядка.
-го порядка.
Плотность распределения случайной величины 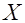 , распределенной по закону Эрланга
, распределенной по закону Эрланга 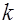 -го порядка, может быть выражена через табличную функцию распределения Пуассона:
-го порядка, может быть выражена через табличную функцию распределения Пуассона:
 ,
,  , (17)
, (17)
где  .
.
Если значение 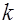 кратно
кратно  и
и  , то гамма-распределение совпадает с распределением хи-квадрат
, то гамма-распределение совпадает с распределением хи-квадрат  .
.
Заметим, что функцию распределения случайной величины 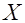 можно вычислить по следующей формуле:
можно вычислить по следующей формуле:
 , (18)
, (18)
где  определяются выражениями (12) и (13).
определяются выражениями (12) и (13).
Следовательно, имеют место равенства, которые нам в дальнейшем пригодятся:
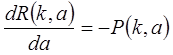 ;
; 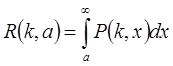 . (19)
. (19)
Пример. Поток производимых на конвейере изделий является простейшим с параметром  . Все производимые изделия контролируются, бракованные укладываются в специальный ящик, в котором помещается не более
. Все производимые изделия контролируются, бракованные укладываются в специальный ящик, в котором помещается не более 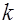 изделий, вероятность брака равна
изделий, вероятность брака равна  . Определить закон распределения времени
. Определить закон распределения времени  заполнения ящика бракованными изделиями и величину
заполнения ящика бракованными изделиями и величину 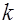 , исходя из того, чтобы ящик с вероятностью
, исходя из того, чтобы ящик с вероятностью  не переполнялся в течение смены.
не переполнялся в течение смены.
Решение. Интенсивность простейшего потока бракованных изделий будет  . Очевидно, что время
. Очевидно, что время  заполнения ящика бракованными изделиями распределено по закону Эрланга
заполнения ящика бракованными изделиями распределено по закону Эрланга
с параметрами  и
и  :
:
 ,
,
следовательно (18) и (19): 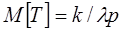 ;
;  .
.
Число бракованных изделий за время 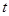 будет распределено по закону Пуассона с параметром
будет распределено по закону Пуассона с параметром 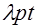 . Следовательно, искомое число
. Следовательно, искомое число 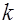 нужно находить из условия
нужно находить из условия  . (20)
. (20)
Например, при  [изделие/ч];
[изделие/ч];  ;
; 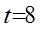 [ч]
[ч]
из уравнения  при
при 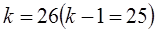
 .
.
Случайная величина, имеющая распределение Эрланга, обладает следующими числовыми характеристиками (табл. 6).
Таблица 6
| Плотность вероятности
|  , ,  ,
где ,
где  – параметр масштаба – параметр масштаба  ; ;
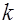 – параметр формы, порядок распределения, целое положительное число – параметр формы, порядок распределения, целое положительное число 
|
| Функция распределения
| 
|
| Характеристическая функция
| 
|
| Математическое ожидание
| 
|
| Мода
| 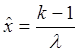
|
| Дисперсия
| 
|
| Асимметрия
| 
|
| Эксцесс
| 
|
| Начальные моменты
|  , , 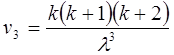 , ,
 , , 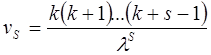
|
| Центральные моменты
|  , , 
|
Заметим, что случайная величина, имеющая нормированное распределение Эрланга  -го порядка, обладает следующими числовыми характеристиками (табл. 7).
-го порядка, обладает следующими числовыми характеристиками (табл. 7).
Таблица 7
| Плотность вероятности
|  , ,  ,
где ,
где  – параметр масштаба – параметр масштаба  ; ;
 – параметр формы, порядок распределения, целое положительное число – параметр формы, порядок распределения, целое положительное число 
|
| Функция распределения
| 
|
| Характеристическая функция
| 
|
| Математическое ожидание
| 
|
| Мода
| 
|
| Дисперсия
| 
|
| Коэффициент вариации
| 
|
| Асимметрия
| 
|
| Эксцесс
| 
|
| Начальные моменты
| 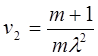 , ,  , ,
 , , 
|
| Центральные моменты
|  , , 
|

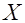 имеет гамма-распределение, если ее плотность распределения выражается формулой
имеет гамма-распределение, если ее плотность распределения выражается формулой ,
,  , (5)
, (5) и
и  ,
,  – гамма-функция:
– гамма-функция: . (6)
. (6)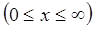 .
. – целое число, то гамма-распределение описывает время, необходимое для появления
– целое число, то гамма-распределение описывает время, необходимое для появления  .
. и
и 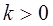 :
:  , (7)
, (7) . (8)
. (8) . (9)
. (9) . (10)
. (10) ,
,  , (11)
, (11)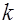 – целое неотрицательное число, то
– целое неотрицательное число, то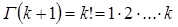 . (12)
. (12) ;
;  . (13)
. (13) и
и  . Определить вероятность восстановления аппаратуры за
. Определить вероятность восстановления аппаратуры за 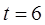 час.
час. .
. функции
функции  , а при
, а при 
 .
. ;
;  , то получим табличный интеграл:
, то получим табличный интеграл: .
. ,
, будет
будет .
. и
и  новые переменные будут равны
новые переменные будут равны  и
и  , а сам интеграл будет равен
, а сам интеграл будет равен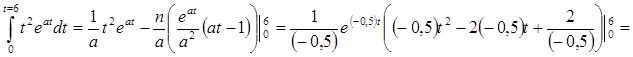
 .
. будет равно
будет равно .
.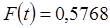 .
. , подчиненной гамма-распределению
, подчиненной гамма-распределению .
. . (14)
. (14) ,
, . (15)
. (15)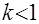 интенсивность отказов монотонно убывает, что соответствует периоду приработки изделия. При
интенсивность отказов монотонно убывает, что соответствует периоду приработки изделия. При  гамма-распределение совпадает с экспоненциальным распределением, при
гамма-распределение совпадает с экспоненциальным распределением, при  гамма-распределение приближается к нормальному закону. Если
гамма-распределение приближается к нормальному закону. Если  ,
, 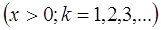 . (16)
. (16) , каждая из которых распределена по показательному закону с параметром
, каждая из которых распределена по показательному закону с параметром 
 , состоящий из суммы
, состоящий из суммы  ,
,  , (17)
, (17) .
. и
и  , то гамма-распределение совпадает с распределением хи-квадрат
, то гамма-распределение совпадает с распределением хи-квадрат  .
. , (18)
, (18) определяются выражениями (12) и (13).
определяются выражениями (12) и (13).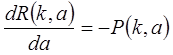 ;
; 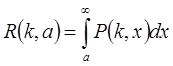 . (19)
. (19) . Определить закон распределения времени
. Определить закон распределения времени  не переполнялся в течение смены.
не переполнялся в течение смены. . Очевидно, что время
. Очевидно, что время  ,
,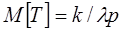 ;
;  .
.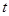 будет распределено по закону Пуассона с параметром
будет распределено по закону Пуассона с параметром 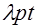 . Следовательно, искомое число
. Следовательно, искомое число  . (20)
. (20) [изделие/ч];
[изделие/ч];  ;
; 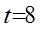 [ч]
[ч] при
при 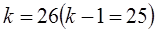
 .
. ,
,  ,
где
,
где  ;
;




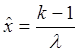



 ,
, 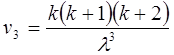 ,
,
 ,
, 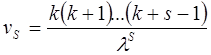
 ,
, 
 -го порядка, обладает следующими числовыми характеристиками (табл. 7).
-го порядка, обладает следующими числовыми характеристиками (табл. 7). ,
,  ,
где
,
где  ;
;
 – параметр формы, порядок распределения, целое положительное число
– параметр формы, порядок распределения, целое положительное число 








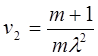 ,
,  ,
,
 ,
, 
 ,
, 



