Функция надежностиБудем называть элементом некоторое устройство независимо от того, «простое» оно или «сложное». Пусть элемент начинает работать в момент времени Таким образом, функция распределения
Функцией надежности Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого
Следовательно, в силу соотношения (41) функция надежности, в случае показательного распределения времени безотказной работы элемента, имеет вид:
Показательным законом надежности называют функцию надежности, определяемую равенством где Как следует из определения функции надежности, эта формула позволяет найти вероятность безотказной работы элемента на интервале времени, длительностью Пример. Время безотказной работы элемента распределено по показательному закону Решение. По условию, постоянная интенсивность отказов Тогда Искомая вероятность того, что элемент проработает безотказно 100 часов, приближенно равна 0, 14. Замечание. Если отказы элементов в случайные моменты времени образуют простейший поток, то вероятность того, что за время
Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Объясняется это тем, что этот закон обладает следующим важным свойством: вероятность безотказной работы элемента на интервале времени Для доказательства свойства введем обозначения событий:
Найдем вероятности этих событий:
Найдем условную вероятность того, что элемент будет работать безотказно на интервале
Полученная формула не содержит Полученный результат можно сформулировать несколько иначе. Сравнив вероятности
|

 , а по истечении времени длительностью
, а по истечении времени длительностью 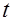 происходит отказ. Обозначим через
происходит отказ. Обозначим через  непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее
непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее  определяет вероятность отказа за время –
определяет вероятность отказа за время –  равна
равна . (21)
. (21) называют функцию, определяющую вероятность безотказной работы элемента за время
называют функцию, определяющую вероятность безотказной работы элемента за время  .
.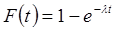 .
. .
. , (22)
, (22) – интенсивность отказов.
– интенсивность отказов. , при
, при  (
( .
. .
. .
. – безотказная работа элемента на интервале
– безотказная работа элемента на интервале  длительностью
длительностью  ;
; – безотказная работа элемента на интервале
– безотказная работа элемента на интервале 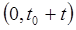 длительностью
длительностью  .
. ,
,  ,
, .
. при условии, что он уже проработал безотказно на предшествующем интервале
при условии, что он уже проработал безотказно на предшествующем интервале  :
: .
. , а содержит только
, а содержит только  и
и  , заключаем: условная вероятность безотказной работы элемента на интервале, длительностью
, заключаем: условная вероятность безотказной работы элемента на интервале, длительностью 


