Пусть дискретная функция  определена при положительных значениях аргумента
определена при положительных значениях аргумента  . Требуется найти такую дискретную функцию
. Требуется найти такую дискретную функцию 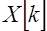 , для которой функция
, для которой функция  является первой разностью. Эта задача аналогична задаче о нахождении первообразной в анализе непрерывных функций. Искомая функция имеет вид
является первой разностью. Эта задача аналогична задаче о нахождении первообразной в анализе непрерывных функций. Искомая функция имеет вид
 , где
, где 
Действительно
 .
.
Функция 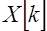 называется первообразной для дискретной функции
называется первообразной для дискретной функции  .
.
Если дискретная функция  определена при всех целочисленных значениях аргумента k=0, ±1, ±2, …, то для определения первообразной необходимо дополнительно потребовать, чтобы при каждом конечном
определена при всех целочисленных значениях аргумента k=0, ±1, ±2, …, то для определения первообразной необходимо дополнительно потребовать, чтобы при каждом конечном  сходился ряд
сходился ряд  . При этом условии первообразная определяется выражением
. При этом условии первообразная определяется выражением
 .
.
Если функция 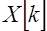 является первообразной для функции
является первообразной для функции  , то и функция
, то и функция  также является первообразной для дискретной функции
также является первообразной для дискретной функции  , где
, где 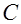 – постоянная величина. Действительно
– постоянная величина. Действительно
 .
.
Таким образом, общий вид первообразной для данной дискретной функции  определяется формулой
определяется формулой
 .
.
Значение постоянной 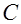 можно выразить через значение первообразной при некотором фиксированном значении аргумента, например при
можно выразить через значение первообразной при некотором фиксированном значении аргумента, например при 
 .
.
Подставляя полученное выражение в формулу (19), найдем
 .
.
Откуда
 (20)
(20)
для любого  .
.
Формула (20) является аналогом соответствующей формулы интегрального исчисления, связывающей интеграл с первообразной, ее можно записать в виде
 , для
, для  . (21)
. (21)
Сумму, стоящую в правой части этого выражения, иногда называют определенной суммой по аналогии с определенным интегралом. Учитывая условие  , можно переписать равенство (21) следующим образом
, можно переписать равенство (21) следующим образом
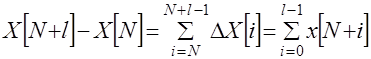 (22)
(22)
или при 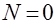
 . (23)
. (23)
Для дискретных функций справедлива формула суммирования по частям, аналогичная формуле интегрирования по частям для обычных функций. Если в формуле (23) положить
 ,
,  .
.
то
 .
.

 определена при положительных значениях аргумента
определена при положительных значениях аргумента  . Требуется найти такую дискретную функцию
. Требуется найти такую дискретную функцию 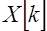 , для которой функция
, для которой функция  , где
, где 
 .
. сходился ряд
сходился ряд  . При этом условии первообразная определяется выражением
. При этом условии первообразная определяется выражением .
. также является первообразной для дискретной функции
также является первообразной для дискретной функции 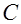 – постоянная величина. Действительно
– постоянная величина. Действительно .
. .
.
 .
. .
. (20)
(20) .
. , для
, для  . (21)
. (21) , можно переписать равенство (21) следующим образом
, можно переписать равенство (21) следующим образом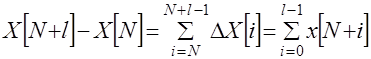 (22)
(22)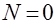
 . (23)
. (23) ,
,  .
. .
.


