ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ТОЧКИ ПО ЕЕ УРАВНЕНИЮ ДВИЖЕНИЯСпособы задания движения точки. Знание законов движения тела означает знание законов движения каждой его точки. Траекторией точки называется множество (геометрическое место) положений движущейся точки в рассматриваемой системе отсчета. В зависимости от формы траектории движение точки бывает двух видов: прямолинейное и криволинейное. Движение точки может быть задано естественным и координатнымм способом. Естественный способ заключается в том, что движение точки задается ее траекторией, началом отсчета и уравнением движения по этой траектории (законом движения) Уравнение движения в общем виде записывается следующим образом:
t — время движения точки от начального момента. Зная траекторию точки и уравнение движения по этой траектории, можно определить положение точки в любой момент времени, для чего следует в равенство Координатный способ заключается в том, что движение точки задается движением ее проекций вдоль осей координат. Уравнения плоского движения точки в координатной форме записываются следующим образом:
Зная уравнения движения точки в координатной форме, можно, подставив в эти уравнения время, определить положение проекций точки, а, следовательно, и самой точки в любой момент времени.
Международная система единиц (СИ) устанавливает в качестве единицы длины метр, а в качестве единицы времени — секунду. Скорость есть кинематическая мера движения точки, характеризующая быстроту изменения ее положения. При равномерном движении скорость измеряется длиной пути, пройденного за единицу времени:
Скорость есть величина векторная. При прямолинейном равномерном движении скорость постоянна и по модулю, и по направлению, а вектор ее совпадает с траекторией (см. рис.). При криволинейном движении скорость точки по направлению меняется. Для того чтобы установить направление вектора скорости при криволинейном движении, разобьем траекторию на бесконечно малые участки пути, которые можно считать вследствие их малости прямолинейными. Тогда на каждом участке условная скорость vп такого прямолинейного движения будет направлена по хорде. В пределе при ∆ s, стремящемся к нулю, хорда совпадаете касательной, следовательно, скорость в каждый момент времени направлена по касательной к траектории в сторону движения (рис. б). При неравномерном движении точки модуль ее скорости меняется. Представим себе точку, движение которой задано естественным способом уравнением Если за небольшой промежуток времени ∆ t точка прошла путь ∆ s, то ее средняя скорость равна Средняя скорость не дает представления об истинной скорости в каждый данный момент времени (истинную скорость иначе называют мгновенной). Чем меньше промежуток времени, за который определяется средняя скорость, тем ближе она к истинной. Истинная скорость есть предел, к которому стремится средняя скорость при ∆ t стремящемся к нулю:
Таким образом, числовое значение скорости равно Истинная скорость при любом движении точки равна первой производной координаты (т. е. расстояния от начала отсчета перемещения) по времени. Движение, в котором скорость с течением времени возрастает, называют ускоренным; движение, в котором скорость с течением времени уменьшается, — замедленным ПРИМЕР: Поезд движется согласно уравнению s = 0, 1t2 + t где t — в секундах, s — в метрах. Определить среднюю скорость поезда за промежуток времени между концом 10-й и 20-й секунд и истинную скорость в конце 20-й секунды. РЕШЕНИЕ. Для определения средней скорости поезда найдем приращения времени и пути за указанный промежуток времени:
Средняя скорость поезда определится так: Для определения истинной скорости поезда продифференцируем уравнение движения по времени, в результате чего получим формулу, выражающую зависимость истинной скорости от времени:
Подставив в это выражение время t2, получим значение истинной скорости в конце 20-й секунды: Ускорение есть кинематическая мера изменения вектора скорости точки. Ускорение есть величина векторная. При прямолинейном движении точки вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости также совпадает с траекторией. Ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени ∆ t скорость точки изменилась на ∆ v, то среднее ускорение Среднее ускорение не дает представления об истинном ускорении в Таким образом, учитывая, что Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от
ЗАДАНИЕ: точка движется по закону s=f(t). Найти ее среднее ускорение в промежутке между моментами t1 и t2, а также ее истинное уускорение в момент времени t3. Данные своего варианта взять из таблицы. Таблица
Составить отчет о практической работе.
|

 где s — расстояние точки от начального положения, являющееся функцией времени;
где s — расстояние точки от начального положения, являющееся функцией времени; подставить время. При своем движении точка проходит некоторый путь, также являющийся функцией времени. Следует подчеркнуть, что путь, пройденный точкой, совпадает с расстоянием от начала отсчета лишь тогда, когда точка все время движется в одном направлении и начало ее движения совпадает с началом отсчета.
подставить время. При своем движении точка проходит некоторый путь, также являющийся функцией времени. Следует подчеркнуть, что путь, пройденный точкой, совпадает с расстоянием от начала отсчета лишь тогда, когда точка все время движется в одном направлении и начало ее движения совпадает с началом отсчета.
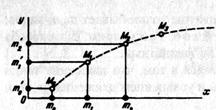 Для того чтобы при координатном способе задания движения точки определить уравнение траектории
Для того чтобы при координатном способе задания движения точки определить уравнение траектории  необходимо из уравнений движения исключить время.
необходимо из уравнений движения исключить время.
 (предполагается, что начала отсчета пути и времени совпадают). Единица скорости
(предполагается, что начала отсчета пути и времени совпадают). Единица скорости
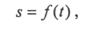










 получаем
получаем 



