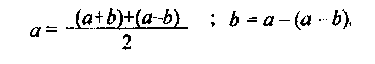ПРОЕКЦИЯХ

Наличие искажений в картографических проекциях, применяемых для географических карт, неизбежно, так как земная поверхность, имеющая форму сфероида, не может быть развернута в плоскость без деформаций: в одних местах возникают разрывы, для устранения которых необходимо равномерное растяжение, в других - перекрытия, требующие равномерного сжатия. Отсюда следует, что на всех географических картах всегда имеются линейные искажения, и масштаб вообще является величиной переменной, меняющейся с изменением места и направления. Наличие искажений длин линий ведет к искажению углов, площадей и форм, хотя имеются картографические проекции, в которых не искажаются ни углы, ни площади.

Различают два вида масштаба длин: а) главный масштаб, который подписывается на карте, представляющий степень уменьшения поверхности земного эллипсоида перед последующим изображением его на плоскости и сохраняющийся в зависимости от применяемой картографической проекции в некоторых точках или линиях, называемых точками и линиями нулевых искажений, и б) частный масштаб, представляющий отношение бесконечно малого отрезка ds в данной точке и по данному направлению к соответствующему бесконечно малому отрезку dS на эллипсоиде, т. е. М = ds/dS. Отношение частного масштаба к главному характеризует искажение длин в данной точке. Иногда в качестве показателя линейных искажений берут не значение частного масштаба, а его отличие от главного, который для данной карты принимается за единицу. При этом величину искажения можно выразить в процентах. Например, пусть М = 1, 45, тогда М-1 = 0, 45 х 100 % = 45 %. Из всех частных масштабов, рассматриваемых в картографии, наибольшее значение имеют масштабы по меридиану m и параллели n.

Главный масштаб площадей показывает, во сколько раз уменьшены площадные размеры поверхности эллипсоида при ее отображении на карте. Частный масштаб представляет отношение бесконечно малой площади на карте к соответствующей бесконечно малой площади на поверхности эллипсоида, т. е. р = dp/dP и является показателем искажения площадей. Его часто, как и показатель длин, выражают в соотносительных величинах. Например, если р = 1, 72, то относительное искажение будет р -1= 1, 72 х100 % = 72 %.

 

Если взять на эллипсоиде кружок бесконечно малого радиуса, то на карте в общем случае он изобразится бесконечно малым эллипсом, называемым эллипсом искажений. Его размеры и форма вполне характеризуют искажения длин, площадей, углов и форм на карте. В равновеликих проекциях площади бесконечно малых круга и эллипса будут одинаковы. В равнопромежуточных проекциях радиус бесконечно малого круга сохранится или по меридиану, или в направлении параллели, в равноугольных проекциях бесконечно малые кружки изобразятся в виде кружков, разных по размеру (см. рис. 2).

Осям эллипса на карте соответствуют два главных взаимно-перпендикулярных диаметра, где наибольший масштаб а совпадает с направлением большой оси, а наименьший в - с направлением малой оси. При совпадении главных направлений с меридианами и параллелями а ~ т, в - п или а - п, a в = m. B тех точках, где меридианы и параллели пересекаются под углами, отличными от 90°, они главными направлениями являться не будут.

Искажения углов заключаются в том, что углы между направлениями на карте не равны соответствующим углам на эллипсоиде. Величина искажения угла в данной точке карты зависит от направления сторон угла. В качестве показателя искажения углов на карте принято наибольшее искажение ω. В любой точке карты всегда имеется угол, изображающийся без искажения и равный 90°, который соответствует главным направлениям эллипса (осям) искажений. Для характеристики искажения углов на карте между меридианом и параллелью, которые на поверхности эллипсоида встречаются под прямым углом, используют его отклонение от 90°, т. е. ε = θ - 90°, где θ - угол между касательными к меридиану и параллели в данной точке.

Искажение длин на карте вызывает также искажение форм К, представляющее отношение большой полуоси эллипсоида к малой, или, что одно и то же, отношение наибольшего масштаба к наименьшему, т. е. К = а/в.

Искажения на картах могут быть определены посредством:

а) измерений по карте с последующими вычислениями;

б) макетов карт с изоколами;

в) номограмм;

г) таблиц.

Отметим, что искажения возрастают с увеличением размеров картографируемой территории и по мере удаления от точек и линий нулевых искажений.

Продолжение табл. 10

Широта в градусах	Длина дуги параллели в 1° по долготе м	Длина дуги меридиана от экватора до параллели м	Широта в градусах	Длина дуги меридиана в 1° по широте м
			20-21
	103 264	2 433 844	21-22
		2 544 583	22-23
	101 753		23-24
			24-25
		2 876 886	25-26
		2 987 683	26-27
		3 098 497	27-28
		3 209 326	28-29
		3 320 172	29-30	1 10 846
		3431 035	30-31
			31-32
			32-33
		3 763 728	33-34
		3 874 662	34-35
			35-36
		4 096 584	36-37
		4 207 573	37-38
			38-39
		4 429 607	39-40	111 027
	84 137	4 540 654	40-41	111 047
		4651 719	41-42
		4 762 804	42-43	111 085
		4 873 908	43-44	111 104
		4 985 032	44-45	111 124
		5 096 176	45-46	111 144
		5 207 339	46-47	111 163
			47^8	111 182
		5 429 723	48^9
		5 540 944	49-50
		- 5652185	50-51
		5 763 445	51-52	111 260
		5 874 723	52-53	111 278
			53-54
		6 097 337	54-55
		6 208 672	55-56	111 335
		6 320 025	56-57'	111 353
		6431 395	57-58	111 370
		6 542 783	58-59	111 388
			59-60	111 406
			60-61	111 423
			61-62	111 439
		6 988 506	62-63

Окончание табл. 10

Широта в градусах	Длина дуги параллели в 1° по долготе м	Длина дуги меридиана от экватора до параллели м	Широта в градусах	Длина дуги меридиана в 1° по широте м
		7 099 978	63-64	111 472
			64-65	111 487
		7 322 967	65-66	1 11 502
			66-67	111 516
	41 822		67-78	111 531
			68 89	111 544
		7769 116	69-70	111 558
		7 880 686	70-71	111 570
		7 992 268	71-72	111 582
		8 103862	72-73	111 594
			73-74	111 605
		8 327 082	74-75	111 615
		8 438 707	75-76	111 625
	25 122		76-77
		8 661 984	77-78	111 643
		8 773 635	78-79	111 651
		8 885 293	79-80	111 658
		8 996 958	80-81	111 665
		9 108 629	81-82	111 671
		9 220 306	82-83	111 677
		9331 987	83-84	111 681
		9 443 673	84-85	111 686
		9 555 362	85-86	111 689
		9 667 053	86-87
		9 778 747	87-88
		9 890 442	88-89	111 695
			89-90	111 695

 

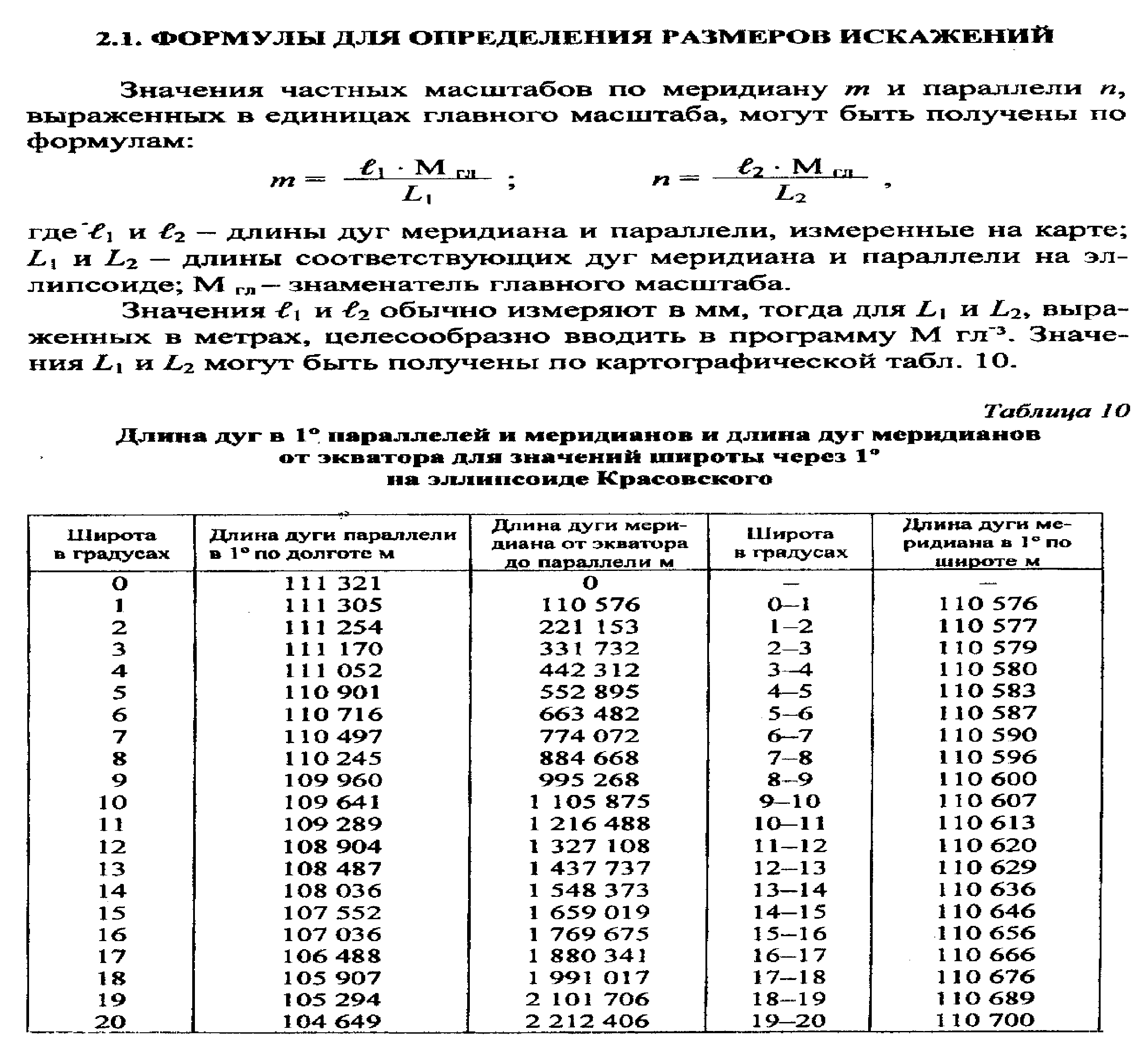
В случае отсутствия таблиц значения L₁ и L₂ могут быть вычислены по формулам математической картографии, которые, учитывая точность измерения по картам, преобразованы нами в более удобный для вычислений вид:

 

где ∆ В ° - разность широт, между которыми вычисляется L₁ и измеряется ℓ ₁ на карте;

- В °т - широта, на которой находится определяемая точка;

- ∆ L ° - разность долгот, между которыми измеряется ℓ ₂

С учетом этого случая для упрощения вычислений разработана программа 2 (табл.12).

Искажение площадей в единицах главного масштаба определяется по формуле

р = тп • sin θ = тп cos ε,

где θ - угол между касательными к меридиану и параллели в определяемой точке;

ε = θ - 90° - величина искажения на карте угла, образованного меридианом и параллелью

 

Максимальное искажение углов вычисляют по формуле, где а и b - наибольший и наименьший масштабы:

 

Отсюда значения наибольшего а и наименьшего b масштабов будут равны:

 

 

Искажение форм можно вычислить по формуле: К = а/b.

Результаты всех вычислений округляют до 0, 01.