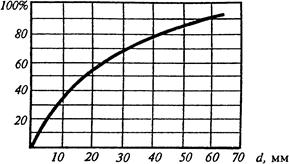
Определение насыпной плотности, гранулометрического состава и угла естественного откоса горных породНасыпная плотность. Для разрушенных горных пород понятия объемная плотность и плотность минерального скелета (твердой фазы) применимы только для отдельных кусков породы. Характеристикой же разрыхленной породы в целом является насыпная плотность. Насыпная плотность rн – это масса единицы объема породы в разрыхленном (раздробленном) состоянии. С учетом насыпной плотности породы рассчитываются погрузочно-транспортные операции на горном предприятии. Для расчета насыпной плотности необходимо знать массу разрыхленной породы и ее объем V (например, объем вагонетки, в которой порода транспортируется), кг/м3: rн = m / V. Насыпная плотность данной породы зависит от коэффициента разрыхления Кр, который всегда больше единицы. Кр = Vр / Vм = rо / rн, где Vр – объем породы в разрыхленном состоянии; Vм – объем породы в монолите. Коэффициент разрыхления (см. табл. 5 прил.) зависит от степени однородности дробления, формы и взаимного расположения кусков разрушенной породы. В действительности разрыхленная порода состоит из кусков и кусочков различной формы и размеров, т.е. из нескольких (многих) фракций. В таком случае свободное пространство между крупными кусками заполняется мелким материалом. Величина Кр становится меньше и зависит от соотношения между размерами наиболее крупных и самых мелких кусков породы и соотношения их объемов. Насыпная плотность и коэффициент разрыхления зависят от ряда внешних факторов: от продолжительности пребывания породы в рыхлом состоянии (от самоуплотнения), давления и влажности породы. Высокий коэффициент разрыхления в большинстве случаев оказывает отрицательное влияние на технологический процесс: снижается степень заполнения ковшей породопогрузочных машин, транспортных средств и бункеров, увеличивается площадь отвалов, складов. При отбойке пород и добыче полезного ископаемого руководствуются определенным соответствием между применяемым горным оборудованием и крупностью кусков разрыхленной породы с учетом необходимости измельчения пород на последующих стадиях переработки. Конкретный размер кусков (оптимальный) породы устанавливается путем экономических расчетов. На практике коэффициент разрыхления определяется с помощью специального металлического ящика размером 1, 0 х 1, 0 х 1, 0м или транспортного сосуда, например, вагонетки. Ящик или кузов вагонетки заполняется доверху породой, а свободное пространство заполняется полностью водой при помощи мерного сосуда. Величина коэффициента разрыхления определяется по формуле: Кр = V / (V – Δ V), где V - объем сосуда; DV - объем воды, используемой на заполнение ящика (вагонетки) с породой. Гранулометрический состав. Практически характер и качество разрушения породы четко определяется ее гранулометрическим составом. Он характеризует разрыхленную горную породу по процентному содержанию в ней частиц различной крупности и может быть изображен кривой (рис. 1.3), если по оси абсцисс откладывается диаметр частиц, а по оси ординат, в процентах - суммарное содержание частиц диаметром, меньшим данного диаметра. Для характеристики неоднородности рыхлых пород используется отношение d60 / d10 = Кн, называемое коэффициентом неоднородности (d60 - максимальный диаметр кусков, составляющих 60%, а d10 - максимальный диаметр кусков, составляющих 10% общего объема рыхлой породы). Гранулометрический состав породы имеет значение при процессах гидромеханизации. От него зависят удельный расход воды на разработку и транспортирование, наименьший допустимый уклон подошвы забоя и лотков, критическая скорость воды.
Рис. 1.3. Кривая гранулометрического состава.
Угол естественного откосаφ о - максимальный угол, образуемый свободной поверхностью рыхлой, раздробленной породы с горизонтальной плоскостью. Частицы породы, находящиеся на этой поверхности, испытывают состояние предельного равновесия. Если вес частицы Р (рис. 1.4.), то в состоянии предельного равновесия на свободной поверхности на частицу действуют силы: Рп - сила нормального давления, прижимающая частицу к свободной поверхности; Рt - сила, стремящаяся сдвинуть частицу вниз; Fт - сила трения, зависящая от величины Рп и коэффициента трения fтр; R - реакция опоры.
Рис. 1.4. Схема к расчету угла и коэффициента трения.
Поскольку частица в равновесии: Рτ - Fт = 0; Р · sin φ о - P· cos φ о · fтр = 0, т.е. tgjо = fтр, arctg fтр = jо. Таким образом, угол естественного откоса зависит от коэффициента трения между кусками породы и поверхностью, по которой возможно ее скольжение. Для рыхлой (сыпучей) среды, например песка, он может быть определен с помощью цилиндрической емкости без дна. Емкость устанавливается на горизонтальной площадке и заполняется породой. Затем цилиндр поднимают и порода формирует свободную поверхность, соответствующую углу естественного откоса. В общем случае угол естественного откоса зависит от шероховатости зерен, степени их увлажнения, гранулометрического состава и формы, а также от плотности материала. С увеличением влажности до некоторого предела у таких горных пород, как уголь или песок, угол естественного откоса возрастает. С увеличением крупности и угловатости частиц он также увеличивается. В целом у рыхлых пород в зависимости от влажности он находится в пределах 0 – 40о. По углам естественного откоса определяются максимальные допустимые углы откосов уступов и бортов карьеров, насыпей, отвалов и штабелей. Упругие свойства горных пород характеризуют их поведение под действием внешних нагрузок. При нагружении порода деформируется - изменяет размеры, форму и объем. При этом в деформируемом объеме породы возникают внутренние силы сопротивления, называемые напряжениями, которые стремятся восстановить прежнюю форму и размеры образца. Если напряжения не превышают определенного значения разного для каждого типа пород, то после снятия нагрузки деформации, вызванные ее действием, исчезают. Такие деформации называются упругими (обратимыми). При этом внутренние силы сопротивления совершают работу, равную работе внешней нагрузки. Если напряжения превышают определенную для разных пород величину, то деформации носят пластический (необратимый) характер. Минимальные напряжения, при которых начинаются пластические деформации, называются пределом упругости породы sЕ. Это один из параметров упругости пород. Остальные параметры, численно оценивающие упругие свойства пород, это коэффициенты пропорциональности между напряжениями и соответствующими им упругими деформациями (рис. 1.5). Деформации, происходящие по направлению действующей силы, называются продольными xl, а перпендикулярно ей - поперечными xd:
где xl - относительная продольная деформация; l0 -длина образца до деформации; l1 - длина образца после деформации; xd - относительная поперечная деформация; d0 - ширина образца до деформации; d1 - ширина образца после деформации,
Рис. 1.5. Деформация образца породы под действием нормальных (а) и касательных (б) сил.
Коэффициент Пуассона m (рис. 1.5 а) является коэффициентом пропорциональности между относительными поперечными xd и относительными продольными x Модуль сдвига G - коэффициент пропорциональности между касательными напряжениями (t)и соответствующей деформацией сдвига (g)(рис 1.5 б): Поскольку коэффициент Пуассона лежит в пределах 0 ¸ 0, 5, модуль сдвига всегда меньше модуля Юнга. Однако для горных пород эта зависимость оказывается более сложной из-за их сложного состава, пористости, влажности и других свойств, что приводит к получению нестабильных показателей и отклонениям от закона Гука, хотя минералы, слагающие породу, этому закону подчиняются. Упругие характеристики некоторых горных пород приведены в табл. 2 приложения.
|



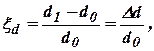
 и
и  - абсолютные деформации.
- абсолютные деформации. Модуль упругости (или модуль Юнга) Е является коэффициентом пропорциональности между действующим нормальным напряжением s и относительной продольной упругой деформацией xl:
Модуль упругости (или модуль Юнга) Е является коэффициентом пропорциональности между действующим нормальным напряжением s и относительной продольной упругой деформацией xl: 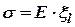 . Для большинства горных пород модуль упругости Е составляет 10 3 - 10 5 MПa и зависит от состава и строения пород.
. Для большинства горных пород модуль упругости Е составляет 10 3 - 10 5 MПa и зависит от состава и строения пород. деформациями: xd = m·x
деформациями: xd = m·x  . Модули упругости связаны между собой зависимостью: G = E/ 2(1+ m).
. Модули упругости связаны между собой зависимостью: G = E/ 2(1+ m).


