Математические модели сигналовПример 1. Случайная величина а) ряд распределения случайной величины б) математическое ожидание в) математическое ожидание двоичного логарифма вероятности Решение. Возможные значения случайной величины равны 1, 2, 3,.... Для осуществления события
Математическое ожидание двоичного логарифма вероятности X также вычисляем по формуле (1.2) [1], положив
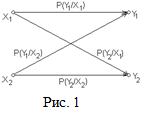
Пример 2. По двоичному каналу связи с помехами (рис. 1) передаются сообщения
б) наиболее вероятное значение в) наиболее вероятное значение Решение. Совместные вероятности сообщения
Безусловные вероятности сигналов на выходе канала вычислим по формуле полной вероятности (1.7) [1]:
Условные вероятности сообщений на входе находим по формуле Байеса (1.9) [1]:
Сравнив Пример 3. Сигнал Осуществить квантование по времени сигнала
найти для квантованного сигнала: а) вектор условных математических ожиданий; б) условную корреляционную матрицу; в) условную плотность вероятности квантованного сигнала на выходе. Решение. Чтобы осуществить квантование непрерывного по времени сигнала Верхняя граничная частота суммы сигнала с шумом равна
Требуемое число отсчетов равно Каждый отсчет сигнала
где
Вектор условных математических ожиданий сигнала состоит из следующих элементов
и определяется только передаваемым сообщением, так как математическое ожидание белого шума Условная корреляционная матрица B сигнала
и равна корреляционной матрице отсчетов шума. Элементы этой матрицы есть отсчеты корреляционной функции шума
Шум стационарен, поэтому его корреляционная функция зависит от разности аргументов
где По условию задачи, он равномерен в полосе 0…
Находим выражение для корреляционной функции
Поскольку
Отсюда видно, что
численно равные дисперсии этих отсчетов (вольт2). Условная плотность вероятности квантованного сигнала есть совместная плотность вероятности системы
Пример 4. Доказать, что для любой положительной случайной величины
Доказать, что для любой системы случайных величин
Найти необходимые и достаточные условия, при которых неравенства обращаются в равенства. Решение. Сначала убедимся, что непрерывная функция Действительно,
Следовательно, график функции
причем знак равенства выполняется только в точке касания Предположим, что
Выбрав абсциссу точки касания
Это неравенство обращается в равенство тогда и только тогда, когда все возможные значения случайной величины Пусть случайная величина
Это неравенство обращается в равенство тогда и только тогда, когда величина
|

 – число бросаний монеты до первого выпадания герба. Найти:
– число бросаний монеты до первого выпадания герба. Найти: необходимо, чтобы в первых
необходимо, чтобы в первых  -1 бросаниях выпадали решетки, а в n -м бросании выпал орел, поэтому
-1 бросаниях выпадали решетки, а в n -м бросании выпал орел, поэтому 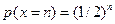 по формуле умножения вероятностей независимых событии. Ряд распределения дан в табл. 1.
по формуле умножения вероятностей независимых событии. Ряд распределения дан в табл. 1. Математическое ожидание числа бросаний вычислим по формуле (1.2) [1], положив
Математическое ожидание числа бросаний вычислим по формуле (1.2) [1], положив ,
,
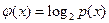 , т. е.
, т. е.
 и
и  с априорными вероятностями
с априорными вероятностями 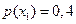 и
и  . Влияние помех описывается переходными вероятностями:
. Влияние помех описывается переходными вероятностями: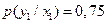 ,
, 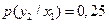 ,
, ,
,  .
. Найти: а) безусловные вероятности сигналов на выходе канала;
Найти: а) безусловные вероятности сигналов на выходе канала; ;
; .
. вычисляем по формуле умножения вероятностей (1.8) [1]:
вычисляем по формуле умножения вероятностей (1.8) [1]:
 ,
,  ,
,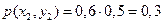 .
. ,
, .
.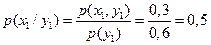 ,
, ,
, ,
, .
. и
и  , видим, что если принят сигнал
, видим, что если принят сигнал  , то более вероятно, что было передано сообщение
, то более вероятно, что было передано сообщение  мог быть с одинаковой вероятностью вызван сообщениями
мог быть с одинаковой вероятностью вызван сообщениями  на выходе непрерывного канала связи выражается через входной сигнал
на выходе непрерывного канала связи выражается через входной сигнал  соотношением
соотношением 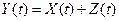 , где
, где  – аддитивный нормальный стационарный белый шум с односторонней спектральной плотностью
– аддитивный нормальный стационарный белый шум с односторонней спектральной плотностью  В/Гц, ограниченный полосой от 0 до
В/Гц, ограниченный полосой от 0 до  МГц. Суммарная мощность составляющих в спектре сигнала
МГц. Суммарная мощность составляющих в спектре сигнала  секунды. Для конкретной реализации входного сигнала (в вольтах)
секунды. Для конкретной реализации входного сигнала (в вольтах)
 в моменты времени
в моменты времени  ,
, 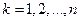 , где
, где  .
.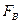 , поэтому шаг квантования определяется в соответствии с теоремой Котельникова
, поэтому шаг квантования определяется в соответствии с теоремой Котельникова мкс.
мкс. .
.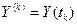 является суммой двух величин
является суммой двух величин ,
, - отсчет сообщения;
- отсчет сообщения; - отсчет шума.
- отсчет шума.
 состоит из следующих элементов
состоит из следующих элементов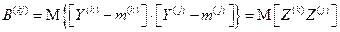
 .
.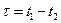 и может быть найдена по теореме Винера – Хинчина (1.21) [1]
и может быть найдена по теореме Винера – Хинчина (1.21) [1] ,
, – спектр плотности мощности шума.
– спектр плотности мощности шума.
 .
. , то
, то .
.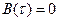 при
при  т.е. отсчеты
т.е. отсчеты  , взятые с шагом квантования
, взятые с шагом квантования 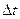 , некоррелированы. Таким образом, в корреляционной матрице отсчетов сигнала не равны нулю будут только элементы, стоящие на главной диагонали,
, некоррелированы. Таким образом, в корреляционной матрице отсчетов сигнала не равны нулю будут только элементы, стоящие на главной диагонали, ,
,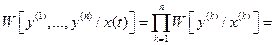

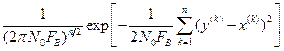 .
. справедливо неравенство Иенсена
справедливо неравенство Иенсена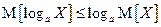 .
. и любой функции
и любой функции  , таких, что
, таких, что  при всех возможных значениях системы, справедливо аналогичное неравенство
при всех возможных значениях системы, справедливо аналогичное неравенство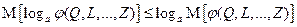 .
. является строго выпуклой вверх, т.е. ее вторая производная отрицательна при любых
является строго выпуклой вверх, т.е. ее вторая производная отрицательна при любых  .
. ,
,  при
при  (рис. 2):
(рис. 2):
 ,
, .
. .
. , получим окончательно
, получим окончательно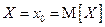 , т.е. если величина X не случайна.
, т.е. если величина X не случайна. , тогда в силу доказанного неравенства имеем
, тогда в силу доказанного неравенства имеем не случайна.
не случайна.


