При изучении спектральных свойств системы нас интересуют стационарные возбужденные состояния, волновые функции которых удовлетворяют заданным граничным условиям на концах цепочки. При этом циклические граничные условия, когда цепочка как бы соединяется в замкнутую петлю, оказываются неудобными для неупорядоченных систем.
Более естественно считать, например, что крайние атомы неподвижны (или, при рассмотрении электронного спектра, что волновые функции обращаются в нуль на концах цепочки) так, что амплитуды  и
и  равны нулю. Это можно рассматривать как частный случай более общего условия, согласно которому при
равны нулю. Это можно рассматривать как частный случай более общего условия, согласно которому при  и
и  степень возбуждения
степень возбуждения  (т. е. отношение двух компонент
(т. е. отношение двух компонент  ), должна принимать наперед заданные значения
), должна принимать наперед заданные значения  и
и  соответственно. Из общей теории задач на собственные значения известно, что если число N достаточно велико, то точные значения
соответственно. Из общей теории задач на собственные значения известно, что если число N достаточно велико, то точные значения  и
и  , как бы мы их ни выбрали, мало влияют на спектр. Следовательно, мы можем без особой ошибки наложить простые, хотя и несколько нефизические условия
, как бы мы их ни выбрали, мало влияют на спектр. Следовательно, мы можем без особой ошибки наложить простые, хотя и несколько нефизические условия  и
и  .
.
С геометрической точки зрения эти условия означают, что при  и
и  двумерный вектор
двумерный вектор  должен располагаться в заданном направлении.
должен располагаться в заданном направлении.
Пока мы рассматриваем только стационарное состояние, можно не обращать внимания на величины последовательных амплитуд возбуждения, а сосредоточиться лишь на исследовании фазы:
 (6.22)
(6.22)
Фаза меняется вдоль цепочки от ячейки к ячейке, удовлетворяя при этом граничным условиям:
 . (6.23)
. (6.23)
Умножение на матрицу переноса  эквивалентно вращению вектора
эквивалентно вращению вектора  . Пользуясь соотношением (6.16), мы можем выразить изменение фазы:
. Пользуясь соотношением (6.16), мы можем выразить изменение фазы:
 (6.24)
(6.24)
через элементы матрицы  и, если аккуратно следовать алгебраическим формулам (17) и (*), то можно, начав с заданного значения
и, если аккуратно следовать алгебраическим формулам (17) и (*), то можно, начав с заданного значения  на одном конце цепочки, вычислить величину
на одном конце цепочки, вычислить величину  на другом конце, последовательно суммируя выражения (6.24).
на другом конце, последовательно суммируя выражения (6.24).
Вообще говоря, определенный таким путем конечный фазовый угол не будет удовлетворять граничному условию (6.23) на конце цепочки. Однако всякая матрица переноса зависит еще от спектральной переменной l. Последняя может входить в  либо явно, как в формуле (6.16), либо по определению переменной lкак энергия «свободного электрона»
либо явно, как в формуле (6.16), либо по определению переменной lкак энергия «свободного электрона»  в формуле (6.21). Иначе говоря, конечную фазу надо написать в виде
в формуле (6.21). Иначе говоря, конечную фазу надо написать в виде  , указывая на зависимость ее от l. Тогда спектр стационарных состояний системы дается набором значений
, указывая на зависимость ее от l. Тогда спектр стационарных состояний системы дается набором значений  , удовлетворяющих условию
, удовлетворяющих условию
 , (6.25)
, (6.25)
где  - целое число. Лишь для этих значений lмы можем одновременно удовлетворить обоим граничным условиям (6.23).
- целое число. Лишь для этих значений lмы можем одновременно удовлетворить обоим граничным условиям (6.23).
Можно доказать общее положение: если собственное значение матрицы переноса вещественны, то в спектре идеальной цепочки имеется «запрещенная зона».
Например, для регулярной модели Кронига - Пенни можно получить неравенство
 , (6.26)
, (6.26)
которое соответствует обычному утверждению: в одномерной цепочке дельта-функций с мощностью 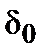 , разнесенных на расстояния
, разнесенных на расстояния  , не существует стационарных состояний с энергией
, не существует стационарных состояний с энергией  (показать самостоятельно).
(показать самостоятельно).
Разумеется, здесь элементы матрицы, переноса содержат периодическую функцию спектральной переменной  . Следовательно, области, в которых удовлетворяется условие (6.26), выступают как промежутки между различными разрешенными зонами. Из условия (6.26) явствует также, что эти запрещенные зоны сужаются по мере роста
. Следовательно, области, в которых удовлетворяется условие (6.26), выступают как промежутки между различными разрешенными зонами. Из условия (6.26) явствует также, что эти запрещенные зоны сужаются по мере роста  .
.

 и
и  равны нулю. Это можно рассматривать как частный случай более общего условия, согласно которому при
равны нулю. Это можно рассматривать как частный случай более общего условия, согласно которому при  и
и  степень возбуждения
степень возбуждения  (т. е. отношение двух компонент
(т. е. отношение двух компонент  ), должна принимать наперед заданные значения
), должна принимать наперед заданные значения  и
и  соответственно. Из общей теории задач на собственные значения известно, что если число N достаточно велико, то точные значения
соответственно. Из общей теории задач на собственные значения известно, что если число N достаточно велико, то точные значения  и
и  .
. (6.22)
(6.22) . (6.23)
. (6.23) эквивалентно вращению вектора
эквивалентно вращению вектора  (6.24)
(6.24) на одном конце цепочки, вычислить величину
на одном конце цепочки, вычислить величину  на другом конце, последовательно суммируя выражения (6.24).
на другом конце, последовательно суммируя выражения (6.24). в формуле (6.21). Иначе говоря, конечную фазу надо написать в виде
в формуле (6.21). Иначе говоря, конечную фазу надо написать в виде  , указывая на зависимость ее от l. Тогда спектр стационарных состояний системы дается набором значений
, указывая на зависимость ее от l. Тогда спектр стационарных состояний системы дается набором значений  , удовлетворяющих условию
, удовлетворяющих условию , (6.25)
, (6.25) - целое число. Лишь для этих значений lмы можем одновременно удовлетворить обоим граничным условиям (6.23).
- целое число. Лишь для этих значений lмы можем одновременно удовлетворить обоим граничным условиям (6.23). , (6.26)
, (6.26)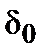 , разнесенных на расстояния
, разнесенных на расстояния  , не существует стационарных состояний с энергией
, не существует стационарных состояний с энергией  . Следовательно, области, в которых удовлетворяется условие (6.26), выступают как промежутки между различными разрешенными зонами. Из условия (6.26) явствует также, что эти запрещенные зоны сужаются по мере роста
. Следовательно, области, в которых удовлетворяется условие (6.26), выступают как промежутки между различными разрешенными зонами. Из условия (6.26) явствует также, что эти запрещенные зоны сужаются по мере роста 


