Уравнениями высших порядковВыясним связь между системой дифференциальных уравнений первого порядка и одним уравнением высшего порядка. Если имеем, например, одно дифференциальное уравнение третьего порядка
то, полагая
Уравнение третьего порядка (3.1) и система (3.2) равносильны в следующем смысле: если Аналогично, имея систему двух уравнений второго порядка
где
Можно показать, что, наоборот, интегрирование системы можно заменить интегрированием одного уравнения высшего порядка. Например, систему трех уравнений первого порядка
можно свести к уравнению третьего порядка относительно
На этом основан метод решения систем дифференциальных уравнений – метод исключения неизвестных. Пример. Рассмотрим систему первого порядка с двумя неизвестными Решение. Используем метод исключения неизвестных, для чего из уравнения (1) выразим
Последнее уравнение – это однородное линейное уравнение второго порядка с постоянными коэффициентами. Характеристическое уравнение
Из (3) находится
Таким образом, общее решение системы имеет вид
где Здесь система из двух уравнений сведена к одному уравнению второго порядка. Сформулируем основные понятия. Определение. Система дифференциальных уравнений второго порядка вида
называется нормальной системой. Определение. Решением системы (3.4) на интервале Определение. Интегралом нормальной системы (3.4) называется функция Определение. Равенство
где Дифференциальное уравнение
можно свести к нормальной системе (3.4). Обратно, система (3.4) в большинстве случаев сводится к дифференциальному уравнению Задача Коши для системы (3.4) ставится следующим образом: найти решение
где Определение. Общим решением системы (3.4) называется совокупность функций
зависящих от Пример. Показать, что определенная равенствами
система функций является общим решением системы уравнений
из предыдущего примера. Решение. В качестве области
Определитель этой системы
Пример. Найти общее решение системы дифференциальных уравнений
и частное решение, удовлетворяющее начальным условиям Решение. Продифференцируем обе части первого уравнения по
В уравнение (2)
Заметим, что
Из уравнения (1) имеем
Итак, общее решение исходной системы имеет вид
Для нахождения частного решения используем начальные условия
Подставив
Рассмотрим еще один метод решения нормальной системы дифференциальных уравнений(3.4), когда она представляет собой систему линейных однородных дифференциальных уравнений с постоянными коэффициентами, т.е. систему вида:
где Рассмотрим систему для n=3
Будем искать частное решение системы (3.8) в виде
где
или
Система (3.10) однородная система линейных уравнений с тремя неизвестными
|

 , (3.1)
, (3.1) , можем заменить это уравнение третьего порядка системой трех уравнений первого порядка
, можем заменить это уравнение третьего порядка системой трех уравнений первого порядка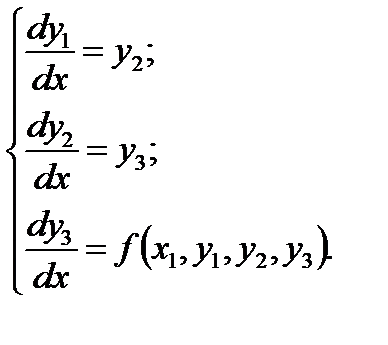 (3.2)
(3.2) - решение уравнения третьего порядка, то
- решение уравнения третьего порядка, то  и
и  есть решение системы (3.2); а если
есть решение системы (3.2); а если  - решение системы, то
- решение системы, то  - решение уравнения третьего порядка (3.1).
- решение уравнения третьего порядка (3.1). (3.3)
(3.3) и
и  - искомые функции от
- искомые функции от  , мы можем заменить ее системой четырех уравнений первого порядка, вводя четыре неизвестные функции
, мы можем заменить ее системой четырех уравнений первого порядка, вводя четыре неизвестные функции  . Прежняя система (3.3) перепишется в виде
. Прежняя система (3.3) перепишется в виде

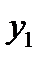 следующего вида
следующего вида .
.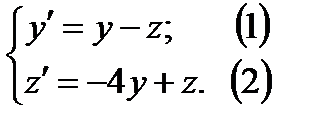
 и продифференцируем полученное выражение:
и продифференцируем полученное выражение:  . Подставим найденные
. Подставим найденные  и
и  в уравнение (2):
в уравнение (2): .
. имеет корни
имеет корни  . Общее решение выписывается по формуле (2.23):
. Общее решение выписывается по формуле (2.23): .
. . Для чего, продифференцировав (4), получим
. Для чего, продифференцировав (4), получим  , следовательно,
, следовательно, .
.
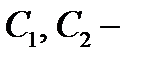 произвольные постоянные.
произвольные постоянные. (3.4)
(3.4) называется совокупность функций
называется совокупность функций 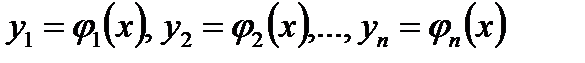 , непрерывно дифференцируемых на
, непрерывно дифференцируемых на 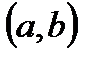 и обращающих уравнения системы (3.4) в тождества относительно
и обращающих уравнения системы (3.4) в тождества относительно 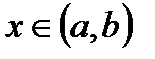 .
. , определенная и непрерывная вместе с частными производными
, определенная и непрерывная вместе с частными производными  в некоторой области
в некоторой области  изменения переменных и принимающая при любых
изменения переменных и принимающая при любых  постоянное значение при подстановке в нее произвольного решения системы.
постоянное значение при подстановке в нее произвольного решения системы.
 - интеграл нормальной системы, а
- интеграл нормальной системы, а  – произвольная постоянная, называется первым интегралом системы (3.4).
– произвольная постоянная, называется первым интегралом системы (3.4). - го порядка
- го порядка
 -го порядка, проинтегрировав которое можно найти и решение исходной системы.
-го порядка, проинтегрировав которое можно найти и решение исходной системы. системы (3.4), удовлетворяющее начальным условиям
системы (3.4), удовлетворяющее начальным условиям (3.5)
(3.5)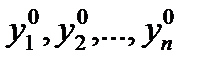 - заданные числа.
- заданные числа. (3.6)
(3.6) произвольных постоянных, которые при любых допустимых значениях постоянных
произвольных постоянных, которые при любых допустимых значениях постоянных  обращают уравнения системы (3.4) в тождества, и в области, в которой выполнены условия теоремы Коши, из совокупности функций (3.6) можно получить решение любой задачи Коши.
обращают уравнения системы (3.4) в тождества, и в области, в которой выполнены условия теоремы Коши, из совокупности функций (3.6) можно получить решение любой задачи Коши. (1)
(1) (2)
(2)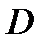 для (2) можно взять область
для (2) можно взять область  ; при этом для любых
; при этом для любых  и
и  из этой области выполнены условия теоремы Коши. Подставив значения
из этой области выполнены условия теоремы Коши. Подставив значения 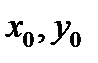 и
и  в систему (1), получим систему уравнений для определения
в систему (1), получим систему уравнений для определения  и
и  :
:
 отличен от нуля при любом
отличен от нуля при любом  . Следовательно, при любых
. Следовательно, при любых 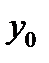 и
и  числа
числа 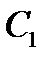 и
и  определяются однозначно, т.е. из системы функций (1) можно получить любое решение задачи Коши для системы дифференциальных уравнений (2).
определяются однозначно, т.е. из системы функций (1) можно получить любое решение задачи Коши для системы дифференциальных уравнений (2).

 .
. , получим
, получим .
. , подставим
, подставим  из (3):
из (3):  . Из уравнения (1) получим
. Из уравнения (1) получим  и, подставив
и, подставив  в
в  , будем иметь
, будем иметь  . Следовательно, система двух уравнений первого порядка свелась к одному уравнению второго порядка
. Следовательно, система двух уравнений первого порядка свелась к одному уравнению второго порядка .
. , поэтому последнее уравнение будет иметь вид:
, поэтому последнее уравнение будет иметь вид:  , откуда
, откуда 

 т.е.
т.е.

 Подставив их в общее решение, получим систему для определения
Подставив их в общее решение, получим систему для определения  и
и  :
:
 в общее решение системы, найдем искомое частное решение
в общее решение системы, найдем искомое частное решение
 (3.7)
(3.7) - постоянные коэффициенты.
- постоянные коэффициенты.
 ,
,  ,
,  (3.9)
(3.9) - постоянные, которые надо подобрать так, чтобы функции (3.9) удовлетворяли системе (3.8). Подставив эти функции в систему и сократив на множитель
- постоянные, которые надо подобрать так, чтобы функции (3.9) удовлетворяли системе (3.8). Подставив эти функции в систему и сократив на множитель  получаем
получаем

 =0 (3.11)
=0 (3.11)


