ТЕОРИЯ ПРОЧНОСТИ КУЛОНА – МОРА
Изученная нами схема одноплоскостного сдвига соответствует частным случаям разрушения грунта в основании сооружения. Более точно этот процесс можно представить, рассмотрев прочность грунта в условиях сложного напряженного состояния. Пусть к граням элементарного объема (рис. 14, а) приложены главные напряжения σ 1 > σ 2 > σ 3 . Если постепенно увеличивать напряжение σ 1 , оставляя постоянной величину σ 3, то в соответствии с теорией Кулона-Мора произойдет сдвиг по некоторой наклонной площадке, причем промежуточное главное напряжение σ 2 никак не влияет на сопротивление грунта сдвигу (рис. 14, б). Как уже известно, на площадке сдвига выполнено условие: τ = σ i · tgφ + с
Рис. 14. К определению прочности грунта в условиях сложного напряженного состояния: а — положение наклонной площадки скольжения; б —распределение напряжений на площадке сдвига
Из курса сопротивления материалов известно, что для площадки, расположенной под углом α;, напряжения равны:
Тогда закон сопротивления сдвигу на этой площадке можно записать в виде
Подставим в это уравнение выражение (46) и продифференцируем, получим выражение
Отсюда следует, что в предельном состоянии в каждой точке грунта имеется две сопряженные площадки скольжения (рис. 15), действующие под углами
Рис. 15. Ориентация площадок скольжения относительно направления действия главных напряжений
|
а б
. (46)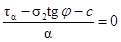
. (47)
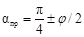. (48)
, 
.
