Определение 2. Элементы  линейного пространства
линейного пространства  называются линейно зависимыми, если найдутся числа
называются линейно зависимыми, если найдутся числа  , не все равные нулю и такие, что
, не все равные нулю и такие, что
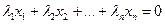 . (1.6)
. (1.6)
Определение 3. Элементы  линейного пространства
линейного пространства  называются
называются
линейно независимыми, если из равенства (1.6) вытекает, что 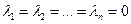 .
.
Свойство линейной зависимости характеризуется предложением.
Предложение 5. Элементы  линейно зависимы тогда и только тогда, когда один из этих элементов может быть представлен в виде линейной комбинации остальных.
линейно зависимы тогда и только тогда, когда один из этих элементов может быть представлен в виде линейной комбинации остальных.
Доказательство. Пусть элементы  линейно зависимы, тогда выполнено (1.6). Причем найдется такой номер
линейно зависимы, тогда выполнено (1.6). Причем найдется такой номер 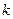 , что
, что  . Поделив (1.6) на
. Поделив (1.6) на 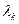 , получим
, получим
 ,
,
откуда, выражая элемент  , получим требуемое представление
, получим требуемое представление
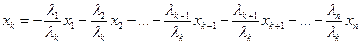 .
.
Верно обратное утверждение. Пусть элемент  является линейной комбинацией остальных, т.е. имеется представление
является линейной комбинацией остальных, т.е. имеется представление
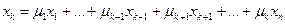 .
.
Отсюда имеем
 .
.
Таким образом, получили соотношение, вида (1.6), с коэффициентом перед  отличным от нуля. Поэтому элементы
отличным от нуля. Поэтому элементы  - линейно зависимы. Предложение доказано.
- линейно зависимы. Предложение доказано.
Определение 4. Если в пространстве  можно найти
можно найти  линейно независимых
линейно независимых
элементов, а любые 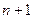 элементов линейно зависимы, то говорят, что пространство
элементов линейно зависимы, то говорят, что пространство  имеет размерность
имеет размерность  .
.
Определение 5. Линейное пространство  , в котором можно указать сколь
, в котором можно указать сколь
угодно большое число линейно независимых элементов, называется бесконечномерным.
Определение 6. Система линейно независимых элементов  линейного пространство
линейного пространство  называется базисом пространства
называется базисом пространства  , если для всякого вектора
, если для всякого вектора  существует разложение
существует разложение
 . (1.7)
. (1.7)
Заметим, что коэффициенты разложения (1.7) определяются однозначно. В самом деле, пусть имеется два разложения
 ,
,
 .
.
Вычитая из одного разложения другое, получим равенство
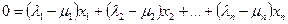 ,
,
из которого в силу линейной независимости элементов  следует, что
следует, что
 .
.
Однозначно определяемые числа  называются координатами вектора
называются координатами вектора  в базисе
в базисе  . Далее имеет место теорема.
. Далее имеет место теорема.
Теорема 1. В пространстве  любая совокупность из
любая совокупность из  линейно независимых элементов пространства
линейно независимых элементов пространства  является базисом этого пространства.
является базисом этого пространства.
Доказательство. Пусть  - система из
- система из  линейно независимых элементов. Возьмем произвольный элемент
линейно независимых элементов. Возьмем произвольный элемент  и рассмотрим совокупность из
и рассмотрим совокупность из 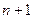 элементов
элементов 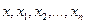 . Она линейно зависима, поскольку число элементов равно
. Она линейно зависима, поскольку число элементов равно 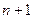 . Поэтому существует соотношение вида
. Поэтому существует соотношение вида
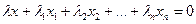 . (1.8)
. (1.8)
Число  . В противном случае получили бы соотношение, вида (1.6), в котором не все числа
. В противном случае получили бы соотношение, вида (1.6), в котором не все числа  равны нулю. А это противоречит условию линейной независимости элементов
равны нулю. А это противоречит условию линейной независимости элементов  . Следовательно
. Следовательно  . Далее из (1.8) имеем
. Далее из (1.8) имеем
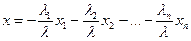 ,
,
т.е. получим необходимое разложение. Теорема доказана.
Следующая теорема является обратной по отношению к теореме 1.
Теорема 2. Если в пространстве  имеется базис, то размерность этого пространства равна числу базисных элементов.
имеется базис, то размерность этого пространства равна числу базисных элементов.
Доказательство. Пусть элементы  образуют базис пространства
образуют базис пространства  . По определению базиса они линейно независимы. Покажем, что любые
. По определению базиса они линейно независимы. Покажем, что любые 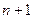 элементов пространства
элементов пространства  линейно зависимы. Рассмотрим
линейно зависимы. Рассмотрим 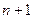 элементов
элементов  и разложим по базису
и разложим по базису
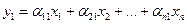 ,
,
 ,
,
……………………………….
 .
.
Далее, записывая в отдельный столбец координаты этих векторов, составим матрицу с  строками и
строками и 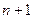 столбцами
столбцами
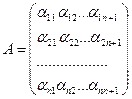
Ранг матрицы 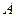 не превосходит
не превосходит  и, как доказывается в линейной алгебре [1,2], один столбец является линейной комбинацией остальных столбцов. В соответствие с этим, один вектор является линейной комбинацией остальных и, согласно предложению 5, элементы
и, как доказывается в линейной алгебре [1,2], один столбец является линейной комбинацией остальных столбцов. В соответствие с этим, один вектор является линейной комбинацией остальных и, согласно предложению 5, элементы  линейно зависимы. Теорема доказана.
линейно зависимы. Теорема доказана.

 линейного пространства
линейного пространства  называются линейно зависимыми, если найдутся числа
называются линейно зависимыми, если найдутся числа  , не все равные нулю и такие, что
, не все равные нулю и такие, что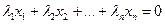 . (1.6)
. (1.6)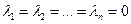 .
.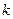 , что
, что  . Поделив (1.6) на
. Поделив (1.6) на 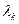 , получим
, получим ,
, , получим требуемое представление
, получим требуемое представление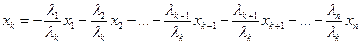 .
.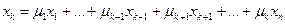 .
. .
. линейно независимых
линейно независимых элементов линейно зависимы, то говорят, что пространство
элементов линейно зависимы, то говорят, что пространство  существует разложение
существует разложение . (1.7)
. (1.7) .
.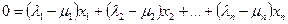 ,
, .
. в базисе
в базисе 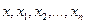 . Она линейно зависима, поскольку число элементов равно
. Она линейно зависима, поскольку число элементов равно 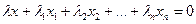 . (1.8)
. (1.8) . В противном случае получили бы соотношение, вида (1.6), в котором не все числа
. В противном случае получили бы соотношение, вида (1.6), в котором не все числа 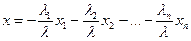 ,
, и разложим по базису
и разложим по базису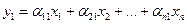 ,
, ,
, .
.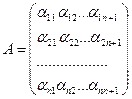
 не превосходит
не превосходит 


