Обратное преобразование Лапласа имеет видf (t) = где j – мнимая единица (j 2 = – 1), а интегрирование в (1.3.2) проводится по бесконечно удаленному контуру комплексной плоскости для действительного значения переменной s. Для практического применения используют таблицы преобразований Лапласа (Web-сайт MCS), полученные на основании выражений (1.3.1) и (1.3.2). Пример показан в таблице 1.3.1. Переменную s в преобразовании Лапласа можно рассматривать как оператор дифференцирования s º Аналогично можно ввести оператор интегрирования
Продемонстрируем использование преобразования Лапласа для решения дифференциальных уравнений (типа 2.1.3) с постоянными коэффициентами. Преобразование Лапласа уравнения (2.1.3) дает в соответствии с таблицей 1.3.1 B [ s 2 Y (s)– sy (0)–d y (0)/d t ]+ C [ sY (s)–y(0)] + DY (s) = X (s). (1.3.5) Если x (t) = 0 (входной сигнал отсутствует), y (0) = y 0 и d y (0)/d t = 0, то Bs 2 Y (s) – Bs y 0 + CsY (s) – Cy 0 + DY (s) = 0. (1.3.6)
Таблица 1.3.1
Выражая отсюда Y (s), получим образ выходного сигнала Y (s) = Если полином q (s) = Bs 2 + Cs + D, стоящий в знаменателе (1.3.7), приравнять нулю, то получим характеристическое уравнение, названное так потому, что его корни (или полюса) определяют характер движения системы. Корни полинома p (s) = (Bs + + C) y 0, стоящего в числителе (1.3.7), называют нулями системы. В полюсах функция Y (s) обращается в бесконечность, а в нулях она становится равной нулю. Расположение полюсов и нулей на комплексной s -плоскости определяет характер собственного (свободного) движения системы. Полином q (s) можно записать в виде q (s) = (s – s 1) (s – s 2), (1.3.8) где s 1 и s 2 – корни полинома. Тогда Y (s) = Пример 1.3.1. Рассмотрим частный случай, когда D / B = 2, а С / B = 3. Тогда выражение (1.3.9) примет вид Y (s) = Положение полюсов и нуля этой функции на s -плоскости показано на рис. 1.3.1, где s = s + jw
Рис. 1.3.1
В общем случае, разложив (1.3.9) на элементарные дроби, получим Y (s) = где k 1 и k 2 – коэффициенты разложения, называемые вычетами. Теперь применим к (1.3.11) обратное преобразование Лапласа y (t) = L-1{ (1.3.12) С помощью таблицы 1.3.1 находим решение y (t) = k 1exp(s 1 t) + k 2 k 1exp(s 2 t) (1.3.13) уравнения (2.1.3) в отсутствии входного воздействия, т.е., так называемое, свободное движение системы. Часто бывает необходимо определить установившееся, или конечное, значение y (t). Теорема о конечном значении гласит, что:
где допускается наличие простого полюса Y (s) в начале координат s -плоскости (см. рис. 1.3.1), но не допускается наличие полюсов на мнимой оси и в правой полуплоскости, а также – кратных полюсов в начале координат. Для примера 1.3.1 Передаточные функции линейных систем. Передаточная функция линейной системы определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при условии, что все начальные значения равны нулю. Передаточная функция существует только для линейных стационарных (с постоянными параметрами) систем и однозначно описывает динамическую связь между выходными и входными переменными. Передаточная функция системы (2.1.3) получается, если в исходном уравнении (1.3.5) все начальные значения положить равными нулю Bs 2 Y (s) + CsY (s) + DY (s) = X (s). (1.3.15) Отсюда находим передаточную функцию
Пример 1.3.2. Передаточная функция RC цепи, изображенной на рис. 1.3.2, получается путем записи в операторной форме уравнений Кирхгофа для напряжений U 1(s) = [ R +1/ Cs ] I (s), (1.3.17) U 2(s) = I (s) / Cs.
Рис. 1.3.2 Тогда из (1.3.17) следует, что
где t = RC есть постоянная времени цепи. Пример 1.3.3. Пусть на вход цепи, изображенной на рис. 1.3.1, подано ступенчатое напряжение c амплитудой U 0 q (t), где q (t) – функция Хевисайда. Как будет изменяться напряжение на выходе цепи? Так как U 1(s) = U 0/ s (см. таблицу 1.3.1), то согласно (1.3.18) U 2(s) = U 1(s) В результате обратного преобразования Лапласа получим u 2(t) = U 0 [1– exp(– t / t)]. (1.3.19) Рассмотрим теперь поведение системы высокого порядка и найдем ее реакцию на входной сигнал после затухания собственного (свободного) движения. Пример 1.3.4. Пусть дифференциальное уравнение движения системы имеет вид y (n) + q n-1 y (n-1) +…+ q 0 y = p n-1 x (n-1) + p n-2 x (n-2) +…+ p 0 x, (1.3.20) где y (t) есть реакция системы, а x (t) – возмущающая функция. Если все начальные значения равны нулю, то вместо дифференциального уравнения (1.3.20) системы запишем его образ по Лапласу s n Y (s) + q n-1 s n-1 Y (s) +…+ q 0 = (1.3.21) = p n-1 s n-1 X (s) + p n-2 s n-2 X (s) +…+ p 0 X (s). Тогда реакция системы состоит из свободного движения, определяемого начальными условиями, и вынужденного движения, обусловленного входным возмущением Y (s) =
|

 , (1.3.2)
, (1.3.2) . (1.3.3)
. (1.3.3) . (1.3.4)
. (1.3.4)

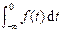
 . (1.3.7)
. (1.3.7) . (1.3.9)
. (1.3.9) . (1.3.10)
. (1.3.10)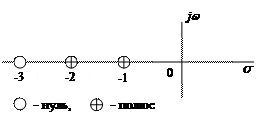
 , (1.3.11)
, (1.3.11)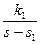 }+L-1{
}+L-1{  }.
}. (1.3.14)
(1.3.14) =0. Тем самым, свободное движение стремится к конечному значению y (t) = 0.
=0. Тем самым, свободное движение стремится к конечному значению y (t) = 0. (1.3.16)
(1.3.16)
 , (1.3.18)
, (1.3.18) = U 0
= U 0 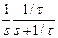 = U 0[
= U 0[  ].
]. , (1.3.22)
, (1.3.22)


