Экспериментальное определение функций распределения случайных величин.ОБОРУДОВАНИЕ: генератор гармонических колебаний, частотомер типа Ч3-54 (Ч3-33), секундомер. ЦЕЛИ РАБОТЫ: экспериментальное определение функций плотности вероятности случайных величин; оценка параметров распределений и влияния случайных факторов на результаты измерений в зависимости от числа измерений; определение условий, в которых наблюдаются нормальное и равномерное распределения. Краткая теория. Событием (случаем) в теории вероятности называют всякое явление, относительно которого имеет смысл ставить вопрос, может оно произойти или нет. Случайные величины могут иметь дискретный спектр значений (например, спектр из шести значений от 1 до 6 при бросании игрального кубика) и непрерывный спектр (определяемая в эксперименте скорость отдельной молекулы – непрерывная случайная величина). Вероятность случайного события характеризует количественную меру ожидаемой возможности его появления. В случае дискретной случайной величины можно дать частотное определение вероятности W случайного события А:
где N – число испытаний, NA - число испытаний, в которых произошло событие А. Очевидно, что задаваемая формулой (1) математическая вероятность может принимать значения от 0 (недостоверное событие) до 1 (достоверное событие). Вычислить среднее значение
здесь n – число различных значений в спектре случайной величины (при бросании игрального кубика оно равно 6), Wi - вероятность выпадения при испытании i –го значения (xi) в спектре случайной величины (например, вероятность выпадения двойки при бросании кубика, равная Таким образом, чтобы вычислить среднее значение дискретной случайной величины, нужно знать спектр ее возможных значений и вероятность каждого значения в спектре. Когда говорят, что дискретная случайная величина задана, то подразумевают, что владеют этой информацией. В случае непрерывной случайной величины частотное определение вероятности не подходит. Например, в отношении скорости отдельной молекулы бессмысленно ставить вопрос о том, чему равна вероятность обнаружить в ходе измерения, что скорость молекулы будет равна 200 здесь dW(х) - вероятность того, что случайная величина в испытании примет значение в интервале dx вблизи данного значения случайной величины x.

Следовательно, функция плотности вероятности равна вероятности обнаружить случайную величину в малом интервале вблизи данного значения величины, отнесенной к величине интервала. Вероятность попасть в малый интервал dx равна
Проведя по формуле (4) вычисление вероятности по всей области определения случайной величины, мы получим вероятность достоверного события, состоящего в том, что в испытании будет зафиксировано какое-либо разрешенное значение случайной величины
Формулу (5) называют условием нормировки вероятности непрерывной случайной величины. Аналогичное условие для дискретной случайной величины получим, заменив интегрирование суммированием
здесь Wi – вероятность выпадения i– го значения в спектре случайной величины, n - число различных значений в спектре. Вычислить среднее значение непрерывной случайной величины можно по формуле, аналогичной формуле (2):
т.е., для определения среднего значения непрерывной случайной величины нужно знать ее функцию плотности вероятности и область определения. Располагая этой информацией говорят, что непрерывная случайная величина задана. В формуле (7) на месте величины х под интегралом, вообще говоря, должна находиться усредняемая величина, роль которой может играть любая функция u(x) аргумента x. Следовательно, среднее значение функции случайной величины можно найти так
Разброс случайной величины относительно среднего значения характеризует дисперсия σ2 - средний квадрат отклонения величины от среднего значения
или, в случае дискретной величины,
На практике дисперсию удобно вычислять по формуле
Результаты непосредственных измерений физической величины часто описываются нормальным распределением (распределением Гаусса)
Еще один пример функции плотности вероятности - прямоугольное (равномерное) распределение, для которого
где β и γ; – границы интервала величины, а
Графики нормального и равномерного распределений представлены на рис.1 и рис.2. Площади, заштрихованные на графиках, равны вероятности обнаружить при испытании значение случайной величины в интервале [ а, b]. Полная площадь под кривой функции плотности вероятности согласно условию нормировки равна единице.
<x> a b x
Рис.1 Нормальное распределение.
f(x)
β <x> a b γ x
Рис.2 Прямоугольное распределение.
На практике число измерений N не бывает достаточным для того, чтобы по их результатам можно было вычислить истинное значение измеряемой величины и дисперсию. Можно лишь найти выборочное среднее
Перед тем, как окончательно записать результат N измерений, нужно определить его надежность, т.е. выяснить с какой вероятностью попадает истинное значение измеряемой величины в данный доверительный интервал. Доверительным интервалом
причем эта запись не означает, что истинное значение измеренной величины лежит в интервале от В ходе лабораторной работы необходимо определить вид функции плотности вероятности, описывающей распределение измеренной в эксперименте случайной величины, и выяснить условия эксперимента, в которых наблюдаются нормальное и прямоугольное распределения. Подготовка к работе.
1. Заземлите приборы. 2. Соедините кабелем выход генератора сигналов с входом «СУММА А» частотомера. 3. Включите приборы тумблером «СЕТЬ». 4. Установите переключатель «РОД РАБОТЫ» в положение «СУММА А». 5. Установите выходную частоту генератора 50-60 Гц. 6. «ПУСК» и «СТОП» осуществляйте клавишей «ПАМЯТЬ». «СБРОС» - соответствующей клавишей на частотомере.
Упражнение 1. (нормальное распределение)
1. При помощи секундомера сделайте 50-60 отсчетов числа импульсов, проходящих через пересчетное устройство частотомера за 5 сек и вычислите ν с точностью до 0.1 имп/сек для каждого отсчета, ν – число импульсов в секунду. Число отсчетов должно нацело делиться на 3. 2. Вычислите среднее значение 3. Для определения вида распределения разбейте весь диапазон из N опытных значений ν на интервалы Δν (в данном случае Δν=0.5с-1). Подсчитайте, какое количество Ni значений попадает в каждый интервал, и вычислите относительную частоту, приходящуюся на единичный интервал. Для этого составьте таблицу:
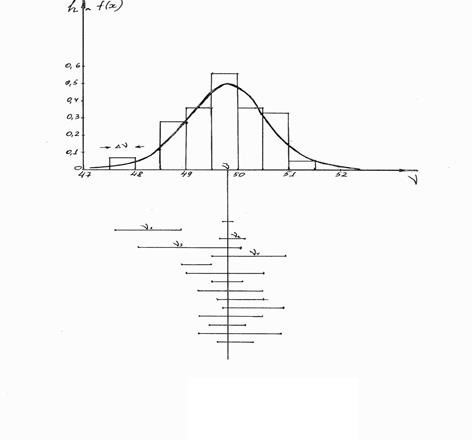
(Цифры в таблице приведены для случая N=51) 4. Построить на миллиметровой бумаге диаграмму распределения плотности вероятности в зависимости от ν, откладывая по оси абсцисс значения ν и Δν, по оси ординат hi. Диаграмма будет представлять систему прямоугольников высотой hi с основаниями Δν (площади которых численно равны доле отсчетов в соответствующем интервале), а площадь всех прямоугольников равна единице. Построенная таким образом диаграмма называется гистограммой. 5. На том же графике и в том же масштабе построить кривую плотности вероятности по уравнению (9), заменив 6. Разбейте полученные ν i -на тройки. Вычислите средние значения, средние квадратичные ошибки, доверительные интервалы для W=0.6 для каждых трех значений (если N=51, то для 17 троек). 7. Нанести для сравнения все средние значения и интервалы на отдельный график в том же масштабе для ν и вычислить, какой процент значений попадает в интервал общего среднего и какой процент интервалов перекрывается с интервалом общего среднего. Оформление результатов упражнения должно быть представлено в виде, данном на рис.3.
Рис.3.
Упражнение 2.
1. На генераторе сигналов установите переключатель «МНОЖИТЕЛЬ» в положение 102. В качестве измеряемой величины используйте последнюю значащую цифру на экране частотомера. Повторите опыт 100 раз. 2. Определите среднее значение и дисперсию. 3. Постройте гистограмму, как и в упражнении 1. В зависимости от вида гистограммы решите вопрос о том, нормальное или прямоугольное распределение плотности вероятности.
Вопросы, которые должны быть рассмотрены при подготовке к сдаче допуска к работе. 1. Основные понятия теории вероятностей. Функция плотности вероятности. 2. В каком случае считают, что дискретная (непрерывная) случайная величина задана? 3. Вычисление средних значений случайных величин. Дисперсия. 4. Прямоугольное и нормальное распределения
Вопросы, которые следует рассмотреть при подготовке к сдаче отчета по работе. 1. При выполнении, каких условий результаты измерений описываются нормальным, прямоугольным распределением? 2. Биномиальное распределение, его предельные формы. 3. Распределение Максвелла, его различные формы. 4. Распределение Больцмана. 5. Вывести формулу (2) и формулу (8//).
Литература.
1. Кондрашов А.П., Шестопалов Е.В. «Основы физического эксперимента и математическая обработка результатов измерений». М., 1977 г. 2. Гнеденко Б.В., Хинчин А.Я. «Элементарное введение в теорию вероятностей». М., 1976 г. 3. Вентцель Е.С. «Теория вероятностей». М., 1964 г. 4. Матвеев А.Н. «Молекулярная физика». М., ВШ., 1981 г.
Таблица 1.
КОЭФФИЦИЕНТЫ СТЬЮДЕНТА tW, N.
ЛАБОРАТОРНАЯ РАБОТА № 6
ИЗУЧЕНИЕ РАБОТЫ ХОЛОДИЛЬНИКА.
Приборы и принадлежности: холодильный агрегат, нагревательный элемент, амперметр, вольтметр, термометр, секундомер. ЦЕЛЬ РАБОТЫ: изучение работы холодильной и тепловой машин.
ВВЕДЕНИЕ.
В данной задаче изучается работа холодильной машины. Холодильная машина – это система, работающая по циклу, обратному тому, по которому работает тепловая машина. Рабочее тело тепловой машины (например, водяной пар в паровом двигателе) участвует в циклическом процессе, в ходе которого получает тепло Qн тела - нагревателя. Часть этого тепла Qх рабочее тело отдает другому телу - холодильнику, температура которого ниже температуры нагревателя. При этом совершается работа над внешними телами, равная
или если считать величины алгебраическими.
Нагреватель с температурой Т1
Qн
Холодильник с температурой Т2 (Т2<T1)
В цикле холодильной машины все величины меняют знак. Это означает, что механическая работа А совершается над рабочим телом. При этом некоторое количество теплоты Q 2 отбирается от теплового резервуара, имеющего меньшую температуру (холодильника), к нему добавляется тепло, связанное с совершенной над рабочим телом работой, и тепло
передается более нагретому телу (нагревателю).
Нагреватель с температурой Т1
Холодильник с температурой Т2 (Т2<T1)
По своей сути, как тепловая, так и холодильная машина являются периодически действующими устройствами, т.е. в ходе их работы рабочее тело периодически повторяет одну и туже последовательность проходимых им состояний. Рассмотрим схему работы изучаемой холодильной машины (рис.1). Рабочим телом машины является фреон CF4. Это жидкость, давление насыщенных паров которой при комнатной температуре составляет около 4 атм. Компрессор М сжимает пары фреона до давления около 10 атм., и они поступают в конденсатор К. При сжатии фреон нагревается, т.к. процесс сжатия идет адиабатически. Конденсатор представляет собой длинную трубку, имеющую хороший тепловой контакт с металлической поверхностью-радиатором. В конденсаторе фреон остается в парообразном состоянии и постепенно охлаждается за счет теплообмена с окружающим воздухом. Радиатор ускоряет процесс охлаждения. Теплообмен ведет к тому, что в последних витках конденсатора температура фреона лишь на 10-150С выше, чем температура окружающего воздуха. Поэтому в последних витках конденсатора часть фреона переходит в жидкое состояние. Далее фреон поступает в испаритель через узкий, длинный капилляр-дроссель Д. Диаметр трубки конденсатора 3-4 мм, а диаметр дросселя 0,8 мм. На входном конце капилляра давление 8 атм., а на выходном около 1 атм. Выходной конец капилляра открывается в испаритель И. Испаритель представляет собой широкую трубку, проложенную в стенках алюминиевого короба. Здесь давление паров фреона оказывается ниже давления насыщенного пара. Фреон закипает. За счет кипения от стен испарителя отнимается тепло. После испарения фреон вновь засасывается компрессором М, проходя через змеевик З, пары фреона на обратном пути охлаждают трубку конденсатора перед испарителем. Это позволяет более эффективно использовать охлаждающие свойства фреона. Компрессор и вся система представляют собой единую замкнутую линию, по которой проходит циркуляция фреона. Эта система изолирована и не сообщается с атмосферой. Компрессор приводит в движение электромотор, питаемый от сети 220 В. В данной задаче измеряется одна из характеристик холодильника – коэффициент эффективности. Т.к. в холодиль-нике совершается превращение механической энергии в «тепловую», то обычное понятие КПД здесь неприменимо. Под коэффициентом эффективности будем понимать отношение количества тепла, отобранного у стенок охлаждаемого тела к количеству энергии, затраченной на этот процесс. В нашем случае эта последняя потребляется в виде электроэнергии. Электрическая схема представлена на рис.2. Здесь охлаждаемым объектом является резервуар с водой Р. В резервуаре находится нагревательный элемент Н и коробка испарителя от холодильного агрегата «Х». Вода в резервуаре перемешивается мешалкой «М», вращаемой мотором. Теплоемкость резервуара с водой может быть определена путем нагревания его. Если нагревательный элемент выделяет в резервуар количество энергии Q и температура резервуара с водой изменяется на ΔТ1, то теплоемкость может быть найдена по формуле
Зная теплоемкость С можно найти коэффициент эффективности холодильной машины. Пусть в течение времени Δt холодильный агрегат понизил температуру резервуара с водой на ΔТ2 градусов. Тогда количество отобранного тепла равно
Если известна совершенная при этом работа, то коэффициент эффективности работы холодильника (холодильный коэффициент):
УПРАЖНЕНИЕ 1. Определение теплоемкости резервуара с водой.
1.Включить мотор мешалки. Выждать 10 мин пока в резервуаре не установится стационарная температура. 2. Включить нагреватель. Для этого тумблер перевести в положение «НАГРЕВ». 3. Включить секундомер. 4. Увеличить температуру воды на один градус. Показания термометра записывать каждые 2 мин. (При такой малой разности температур воды и воздуха теплообменом между ними можно пренебречь.) 5. Мощность W потребляемой электроэнергии измеряется по показаниям вольтметра и амперметра. Записывать показания приборов через каждые 2 минуты. 6. Выключить нагреватель, продолжая фиксировать температуру. 7. Показания термометра записывать до тех пор, пока температура не станет уменьшаться. (При выключенном нагревателе.) 8. Построить график зависимости температуры от времени. 9. Найти полное приращение температуры воды ΔТ1. 10. Рассчитать количество энергии, затраченное на нагрев и теплоемкость резервуара с водой по формуле (3).
УПРАЖНЕНИЕ 2. Определение коэффициента эффективности.
1. Включить холодильник. Для этого тумблер перевести в положение «ХОЛ». 2. Включить секундомер. 3. Понизить температуру воды на один градус относительно комнатной. Показания термометра записывать через 2 мин. В ходе охлаждения резервуара с водой записывать показания вольтметра и амперметра через каждые 2 минуты. 4. Выключить холодильник. 5. Показания термометра фиксировать до тех пор, пока температура не станет расти. (При выключенном холодильнике). 6. Выключить мотор мешалки. 7. Построить график зависимости температуры от времени. 8. Найти полное приращение температуры ΔТ2 . 9. Построить график зависимости потребляемой холодильником мощности от времени. 10. По графику найти полную энергию, затраченную на работу холодильника. Полная энергия равна сумме: Пользуясь этим выражением и формулой (4) рассчитать коэффициент эффективности холодильника. Данные опыта занести в таблицу:
Теоретические вопросы, которые следует разобрать при подготовке к сдаче допуска к работе.
1. Тепловая машина, ее КПД. 2. Холодильник и нагреватель, их коэффициенты эффективности. 3. Работа, количество теплоты, внутренняя энергия.
Вопросы, которые должны быть разобраны при подготовке к сдаче отчета.
1. Различные формулировки основного постулата второго начала термодинамики. 2. Теоремы Карно, их доказательство. 3. Третье начало термодинамики в формулировке Планка. Его объяснение на основе формулы Больцмана для энтропии. 4. «Тепловая смерть» Вселенной.
ЛИТЕРАТУРА.
1. Кикоин Н.К., Кикоин К.К. «Молекулярная физика», гл.7. Физматизд., 1962 г. 2. Телеснин Р.В. «Молекулярная физика». 3. Матвеев А.Н.Молекулярная физика. ВШ. 1981.
М R
Рис.1
Р
Рис.2
ЛАБОРАТОРНАЯ РАБОТА № 8
|

 , (1)
, (1)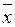 дискретной случайной величины можно по формуле
дискретной случайной величины можно по формуле , (2)
, (2) ).
).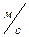 , ведь число возможных значений скорости бесконечно. Непрерывную случайную величину х описывают с помощью функции плотности вероятности
, ведь число возможных значений скорости бесконечно. Непрерывную случайную величину х описывают с помощью функции плотности вероятности 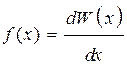 , (3)
, (3) , а вероятность того, что при испытании случайная величина окажется в конечном интервале [ x1; x2 ]
, а вероятность того, что при испытании случайная величина окажется в конечном интервале [ x1; x2 ] . (4)
. (4) (5)
(5)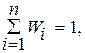 (6)
(6)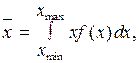 (7)
(7)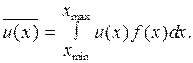 (7/)
(7/)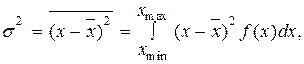 (8)
(8) (8/)
(8/) (8//).
(8//).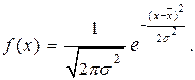 (9)
(9)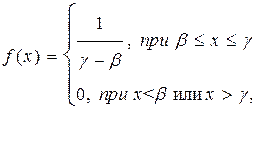 (10)
(10)

 f(x)
f(x)







 для серии из N измерений и выборочное среднее квадратичное отклонение среднего значения SN по формулам:
для серии из N измерений и выборочное среднее квадратичное отклонение среднего значения SN по формулам: 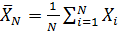 (12)
(12)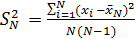 (13)
(13)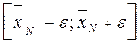 называют интервал, в котором находится с заданной вероятностью истинное значение измеренной величины. Под абсолютной ошибкой ε; в теории обычно понимают величину tW, N SN, где tW, N - коэффициент Стьюдента, значение которого зависит от вероятности попадания измеренной величины в доверительный интервал и от проведенного числа измерений. Значения коэффициента Стьюдента приведены в таблице 1. Таким образом, результат представляется в виде:
называют интервал, в котором находится с заданной вероятностью истинное значение измеренной величины. Под абсолютной ошибкой ε; в теории обычно понимают величину tW, N SN, где tW, N - коэффициент Стьюдента, значение которого зависит от вероятности попадания измеренной величины в доверительный интервал и от проведенного числа измерений. Значения коэффициента Стьюдента приведены в таблице 1. Таким образом, результат представляется в виде: (15)
(15) до
до  а лишь указывает на то, что истинное значение попадает в этот интервал с вероятностью W.
а лишь указывает на то, что истинное значение попадает в этот интервал с вероятностью W. и среднеквадратичное отклонение среднего SN по формулам (12) и (13) и интервал для надежности W=0.6 пользуясь таблицей 1.
и среднеквадратичное отклонение среднего SN по формулам (12) и (13) и интервал для надежности W=0.6 пользуясь таблицей 1.
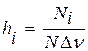
 и σ2 их оценками
и σ2 их оценками 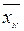
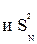 . Вычислить координаты для абсцисс равных
. Вычислить координаты для абсцисс равных  и
и 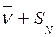 .
.
 (1)
(1)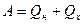 , (1э)
, (1э)

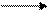 р.т.
р.т.
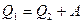 (2)
(2)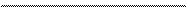
 р.т. А
р.т. А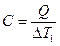 . (3)
. (3)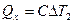
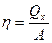 . (4)
. (4) , вычисляющейся для всех двухминутных интервалов работы холодильника.
, вычисляющейся для всех двухминутных интервалов работы холодильника.




 И
И


 М
М

 Ваттметр
Ваттметр


 Х Н
Х Н




 ~ 220В
~ 220В






