15. Пусть X и Y – два множества, состоящие из вещественных чисел. Тогда, если для любых чисел  и
и 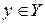 выполняется неравенство
выполняется неравенство 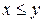 , то существует хотя бы одно число c, такое, что для любых чисел x и y выполняются неравенства
, то существует хотя бы одно число c, такое, что для любых чисел x и y выполняются неравенства
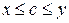 .
.
Следует заметить, что свойством непрерывности обладает множество всех вещественных чисел, но им не обладает множество только рациональных чисел. Действительно, пусть множество X состоит из рациональных чисел x, для которых выполняется неравенство  , а множество Y состоит из рациональных чисел y, для которых выполняется неравенство
, а множество Y состоит из рациональных чисел y, для которых выполняется неравенство  . Тогда, очевидно, для любого числа
. Тогда, очевидно, для любого числа  и любого числа
и любого числа 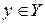 выполняется неравенство
выполняется неравенство  . Однако, не существует рационального числа c такого, чтобы выполнялись неравенства
. Однако, не существует рационального числа c такого, чтобы выполнялись неравенства  . В самом деле, таким числом могло бы быть только
. В самом деле, таким числом могло бы быть только 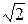 , которое, но оно не является рациональным.
, которое, но оно не является рациональным.
Теперь окончательно будем считать, что вещественные числа представляют собой множество элементов, обладающих свойствами 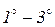 . Такое определение вещественных чисел называется аксиоматическим, а свойства
. Такое определение вещественных чисел называется аксиоматическим, а свойства 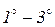 аксиомами вещественных чисел.
аксиомами вещественных чисел.
В дальнейшем нам придется иметь дело с различными множествами вещественных чисел. Всюду, где это не может привести к неточности, для краткости вещественные числа будем называть просто числами.
Если 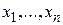 – произвольные числа, то запись
– произвольные числа, то запись 
 означает, что число x максимальное (минимальное) из чисел
означает, что число x максимальное (минимальное) из чисел 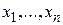 .
.
Приведем наиболее употребляемые числовые множества. Пусть  и
и 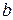 – два числа, причем
– два числа, причем  . Будем использовать следующие обозначения:
. Будем использовать следующие обозначения:
 - отрезок;
- отрезок;
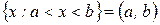 - интервал;
- интервал;
 ;
; 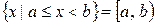 - полуинтервалы;
- полуинтервалы;
 ;
; 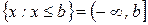 - лучи;
- лучи;
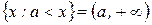 ;
; 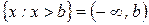 - лучи.
- лучи.
R = 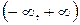 - множество вещественных чисел
- множество вещественных чисел
Все эти множества будем называють промежутками и обозначать X. Промежутки  ,
, 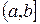 ,
,  и
и 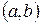 называются конечными;
называются конечными;  и
и 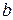 – их концы. Остальные промежутки называются бесконечными.
– их концы. Остальные промежутки называются бесконечными.
Интервал 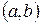 отличается от отрезка
отличается от отрезка  лишь тем, что ему не принадлежат концы
лишь тем, что ему не принадлежат концы  и
и 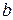 . Это отличие играет существенную роль во многих вопросах математического анализа. Кроме того, интервал
. Это отличие играет существенную роль во многих вопросах математического анализа. Кроме того, интервал 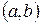 не содержит ни наибольшего, ни наименьшего числа, в то время как в отрезке
не содержит ни наибольшего, ни наименьшего числа, в то время как в отрезке  такими числами являются соответственно
такими числами являются соответственно 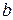 и
и  . Примером промежутка является
. Примером промежутка является 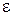 - окрестность точки
- окрестность точки 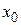 ,это множество
,это множество 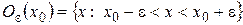 , где
, где 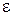 некоторое положительное число.
некоторое положительное число.
Определение. Множество 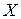 называется ограниченным сверху (снизу), если существует число М такое, что для любого
называется ограниченным сверху (снизу), если существует число М такое, что для любого  выполняется неравенство
выполняется неравенство  .
.
Число  в этом случае называется верхней (нижней) гранью множества. Множество, ограниченное и сверху и снизу, называется ограниченным.
в этом случае называется верхней (нижней) гранью множества. Множество, ограниченное и сверху и снизу, называется ограниченным.
Например, любой конечный промежуток ( ,
, 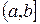 ,
,  ,
, 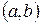 ) ограничен,
) ограничен,
интервал 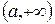 есть множество, ограниченное снизу, но не ограниченное сверху, а интервал
есть множество, ограниченное снизу, но не ограниченное сверху, а интервал 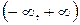 есть множество, не ограниченное ни сверху, ни снизу.
есть множество, не ограниченное ни сверху, ни снизу.

 и
и 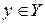 выполняется неравенство
выполняется неравенство 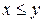 , то существует хотя бы одно число c, такое, что для любых чисел x и y выполняются неравенства
, то существует хотя бы одно число c, такое, что для любых чисел x и y выполняются неравенства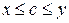 .
. , а множество Y состоит из рациональных чисел y, для которых выполняется неравенство
, а множество Y состоит из рациональных чисел y, для которых выполняется неравенство  . Тогда, очевидно, для любого числа
. Тогда, очевидно, для любого числа  . Однако, не существует рационального числа c такого, чтобы выполнялись неравенства
. Однако, не существует рационального числа c такого, чтобы выполнялись неравенства  . В самом деле, таким числом могло бы быть только
. В самом деле, таким числом могло бы быть только 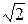 , которое, но оно не является рациональным.
, которое, но оно не является рациональным.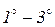 . Такое определение вещественных чисел называется аксиоматическим, а свойства
. Такое определение вещественных чисел называется аксиоматическим, а свойства 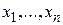 – произвольные числа, то запись
– произвольные числа, то запись 
 означает, что число x максимальное (минимальное) из чисел
означает, что число x максимальное (минимальное) из чисел  и
и 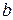 – два числа, причем
– два числа, причем  . Будем использовать следующие обозначения:
. Будем использовать следующие обозначения: - отрезок;
- отрезок;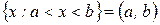 - интервал;
- интервал; ;
; 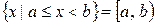 - полуинтервалы;
- полуинтервалы; ;
; 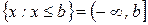 - лучи;
- лучи;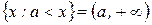 ;
; 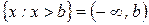 - лучи.
- лучи.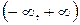 - множество вещественных чисел
- множество вещественных чисел  ,
, 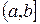 ,
,  и
и 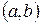 называются конечными;
называются конечными; 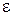 - окрестность точки
- окрестность точки 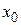 ,это множество
,это множество 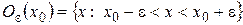 , где
, где 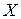 называется ограниченным сверху (снизу), если существует число М такое, что для любого
называется ограниченным сверху (снизу), если существует число М такое, что для любого  выполняется неравенство
выполняется неравенство  .
. в этом случае называется верхней (нижней) гранью множества. Множество, ограниченное и сверху и снизу, называется ограниченным.
в этом случае называется верхней (нижней) гранью множества. Множество, ограниченное и сверху и снизу, называется ограниченным.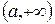 есть множество, ограниченное снизу, но не ограниченное сверху, а интервал
есть множество, ограниченное снизу, но не ограниченное сверху, а интервал 


