Температурное поле непрерывного неподвижного точечного источника в неограниченной среде. Функция ошибок Гаусса (функция erf(х)).Если в точке с координатами x', y', z' в интервале времени от t' = 0 до t' = t работает источник тепла мощностью W, то температурное поле этого источника может быть найдено интегрированием фундаментального решения по t' от 0 до t (т.е. от момента включения до момента выключения источника). Поместим начало координат в точку, где находится источник тепла. Тогда x' = y' = z' = 0, и формула для температуры принимает вид:
где r2 = (x - x')2 + (y - y')2 + (z - z')2 = x2 + y2 + z2 - квадрат расстояния от источника до точки наблюдения. Произведем в интеграле (1) замену переменных: r2/[4a(t - t')] = a2. Тогда: (t - t')3/2 = r3/(8a3/2a3), dt' = r2da/(2aa3), пределы интегрирования: t' = 0 ®
Первый интеграл, стоящий в скобках, известен из курса высшей математики:
Через эту функцию выражаются решения многих задач в теории теплопроводности, да и в других областях физики она играет важную роль. Из определения (3) видно, что erf(0) = 0, а erf(¥) = 1, т.е. erf(x) - это монотонно возрастающая функция, вид которой изображен на рисунке. Функция erf(x) табулирована, и ее значения приводятся в различных справочниках. В библиотеках некоторых языков программирования имеются готовые подпрограммы для вычисления функции erf(x). Если готовой подпрограммы нет, функцию erf(x) можно вычислить с помощью степенного ряда. "Стандартное" разложение этой функции в степенной ряд, которое обычно приводится в математических справочниках, имеет вид:
Этот ряд удобен для анализа свойств функции, но для практических расчетов он неудобен, т.к. является знакопеременным, что при вычислениях приводит к потере точности. Более удобен следующий ряд:
где
С помощью этого ряда легко составить программу вычисления erf(x) на любом языке программирования и даже на программируемом микрокалькуляторе. Суммирование надо прекращать, когда при добавлении очередного an -го слагаемого сумма перестанет меняться (будет достигнута "машинная точность"). Если большой точности не требуется, то можно использовать приближенную формулу: erf(x)» [1 - exp(-4x2/p)]1/2. (6) Формула (6) дает значения, абсолютная погрешность которых не более 6.3×10-3, а относительная погрешность не более 0.71%. Иногда требуется определить erf(x) в области отрицательных значений x. Из формулы (3) очевидно, что erf(-x) = - erf(x). С функцией erf(x) связано еще несколько функций, часто встречающихся в теплофизических задачах. Это прежде всего дополнительный интеграл вероятностей:
который встречается настолько часто, что для него используется специальное обозначение: erfc(x) (сокращенно читается "эрфик"). Вид этой функции также приведен на рисунке. Довольно часто функцию erf(x) приходится дифференцировать и интегрировать. Из определения (3) следует, что
а интеграл от erfc(x) (обозначается как ierfc(x)) равен:
Вернемся к формуле (2). Замечая, что rca = l, запишем эту формулу в виде:
При t ® ¥ значение функции
|

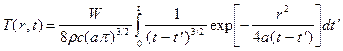 , (1)
, (1)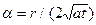 , t' = t ® a = ¥;, и формула (1) принимает вид:
, t' = t ® a = ¥;, и формула (1) принимает вид: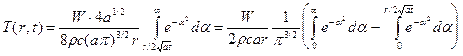 . (2)
. (2) (интеграл Пуассона),
(интеграл Пуассона), а второй интеграл через элементарные функции не выражается и определяет специальную функцию, которая называется функцией ошибок Гаусса, или интегралом вероятностей, или функцией эрфектум:
а второй интеграл через элементарные функции не выражается и определяет специальную функцию, которая называется функцией ошибок Гаусса, или интегралом вероятностей, или функцией эрфектум: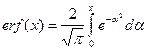 . (3)
. (3)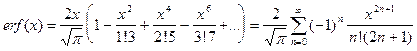 . (4)
. (4) , (5)
, (5) ,
, 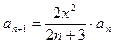 .
.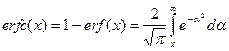 , (7)
, (7) , (8)
, (8) . (9)
. (9)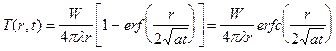 . (10)
. (10) ® 0,
® 0, 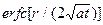 ® 1, и формула (10), как и должно быть, совпадает с формулой для стационарного решения (если T0 принять за начало отсчета температуры), т.к. при t ® ¥ достигается стационарное распределение температуры в безграничной среде.
® 1, и формула (10), как и должно быть, совпадает с формулой для стационарного решения (если T0 принять за начало отсчета температуры), т.к. при t ® ¥ достигается стационарное распределение температуры в безграничной среде.


