Непрерывность функций. Точки разрывa.Функция 1) эта функция определена в некоторой окрестности точки а; 2) существует предел 3) этот предел равен значению функции в точке а, т.е. Обозначая Если функция непрерывна в каждой точке некоторой области, то она непрерывна в этой области. Точка а, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается условие непрерывности функции. Если существуют конечные пределы
Точки разрыва I рода подразделяются на точки устранимого разрыва (когда f(a-0) = f(a + 0)≠ f (a)) и точки скачка (когда f(a - 0) ≠ f(a + 0)), f(a + 0)-f(a-0)) - скачок функции в точке а. Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода. В точках разрыва II рода не существует хотя бы один из односторонних пределов.
Пример 1. Доказать, что функция Область определения нашей функции D(f) = (- f(2) = 2, Условие
Пример 2. Доказать, что функция Для доказательства непрерывности функции на (- Область определения нашей функции - вся числовая ось. Δ f = f (x + Δ х)- f (x) = (7( + 7 Δ
Следовательно, f (x)=7 x 2-3 непрерывна в любой точке интервала
Пример 3. Исследовать на непрерывность функцию
Рис. 7 Всякая элементарная функция непрерывна в своей области определения. Данная функция задается различными формулами на разных участках, следовательно, не является элементарной. Однако, если разбить область определения D(f)= Таким образом, осталось исследовать граничные точки.
1) x1 =0, f(x1)= f(x2)=0
Таким образом, в точке х1, функция непрерывна.
2)
Пределы слева и справа в точке
Пример 4. Найти и классифицировать точки разрыва функции y= В точках 1)
2)
Обе точки Пример 5. Показать, что при х=3 функция у = В точке,
Функция в точке Он будет устранен, если условиться, что при
Задания для самостоятельной работы. 1) Исследовать на непрерывность f(x)=
2) Доказать непрерывность функции f(x) =
3) Исследовать на непрерывность функцию:
4) Исследовать характер точки разрыва функции
5)Найти точки разрыва: а) Список литературы 1.Пискунов Н.С. Дифференциальное и интегральное исчисления – М.: “ Интеграл-пресс ”,1997-416с. 2.Данко П.Е. и др. Высшая математика в задачах и упражнениях. Ч.1./ П.Е. Данко и др. – М.: Высшая школа, 1986 – 306 с.
Учебное издание
|

 называется непрерывной в точке а, если
называется непрерывной в точке а, если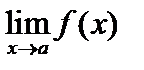 ;
; .
.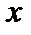 - а =Δx и f(x)- f(a) =Δy, условие непрерывности можно записать так:
- а =Δx и f(x)- f(a) =Δy, условие непрерывности можно записать так:  Δy = 0.
Δy = 0.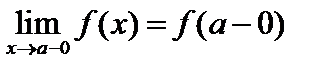 и
и 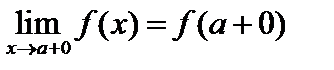 , причем не все три числа f(a), f(a - 0), f(a + 0), равны между собой, то а называется точкой разрыва I рода.
, причем не все три числа f(a), f(a - 0), f(a + 0), равны между собой, то а называется точкой разрыва I рода.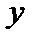 = З
= З 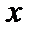 -4 непрерывна в точке
-4 непрерывна в точке 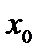 =2.
=2.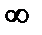 ;+
;+  ),
),  следовательно функция определена в точке x0 и в окрестности точки
следовательно функция определена в точке x0 и в окрестности точки  .
.
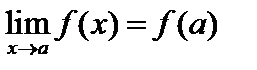 выполнено, следовательно, данная функция непрерывна в точке
выполнено, следовательно, данная функция непрерывна в точке  =2.
=2. = 7
= 7  2 -3 непрерывна на интервале (-
2 -3 непрерывна на интервале (-  ;+
;+  ).
).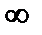 ;+
;+  ) надо доказать непрерывность ее в произвольной точке х
) надо доказать непрерывность ее в произвольной точке х  (-
(-  ;+
;+  ), надо доказать
), надо доказать  Δy = 0.
Δy = 0.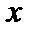 + Δ
+ Δ 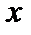 )2 -3)-(7
)2 -3)-(7 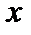 2 - 3) = 7 х 2 + 14 х Δ х +
2 - 3) = 7 х 2 + 14 х Δ х + 2 - 3 - 7 х 2 + 3 = 14
2 - 3 - 7 х 2 + 3 = 14 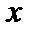 Δ
Δ  + 7Δ
+ 7Δ 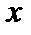 2 = 7Δ
2 = 7Δ  (2
(2  + Δ х)
+ Δ х) Δy =
Δy = 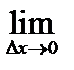 7Δ
7Δ 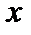 (2
(2  + Δ х) = 0
+ Δ х) = 0 и тогда непрерывна на всем интервале.
и тогда непрерывна на всем интервале.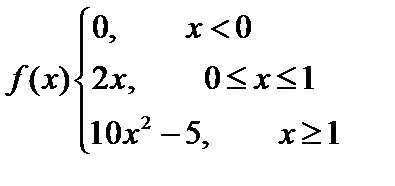
 на отдельные интервалы D1(f) =
на отдельные интервалы D1(f) =  ;.D2(f) =
;.D2(f) =  ; D 3(f)=
; D 3(f)=  ,то на каждом из этих интервалов функция f(x) окажется элементарной и, следовательно, непрерывной.
,то на каждом из этих интервалов функция f(x) окажется элементарной и, следовательно, непрерывной.
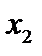 = 1
= 1

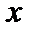 2 не равны между собой, таким образом, точка
2 не равны между собой, таким образом, точка 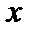 2 - точка разрыва 1 рода.
2 - точка разрыва 1 рода.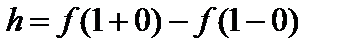 =5-2=3- скачок функции в точке
=5-2=3- скачок функции в точке  2.
2.
 =1 и
=1 и  =5 функция не определена.
=5 функция не определена.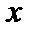 = 1
= 1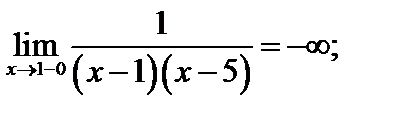

 =5
=5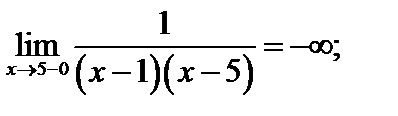

 =1 и
=1 и 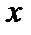 =5 - точки разрыва II рода.
=5 - точки разрыва II рода.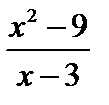 имеет устранимый разрыв.
имеет устранимый разрыв. =3 функция не определена. В других точках дробь можно сократить на
=3 функция не определена. В других точках дробь можно сократить на  -3≠0, следовательно, у = х + 3 во всех точках х≠З,
-3≠0, следовательно, у = х + 3 во всех точках х≠З,
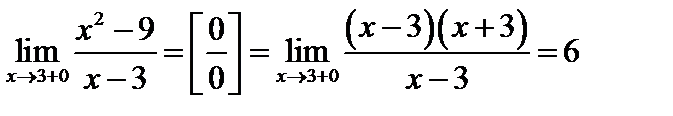
 =3 имеет устраняемый разрыв.
=3 имеет устраняемый разрыв.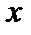 =3 значение функции равно 6.
=3 значение функции равно 6.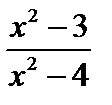 точке
точке 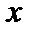 0=2;
0=2; + ln(l + х) в области (-1;+оо);
+ ln(l + х) в области (-1;+оо);
 ;
;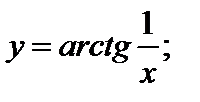 б)
б) 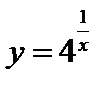 .
.


