Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Приклад визначення ризику
Дата добавления: 2015-10-19; просмотров: 531
|
|
Обширную группу методов уточнения корня представляют итерационные методы - методы последовательных приближений. Здесь в отличие от метода дихотомии задается не начальный интервал местонахождения корня, а его начальное приближение.
Наиболее популярным из итерационных методов является метод Ньютона (метод касательных).
|
| Рис. 3. Метод касательных |
Пусть известно некоторое приближенное значение Zn корня X*. Применяя формулу Тейлора и ограничиваясь в ней двумя членами, имеем
,
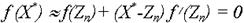откуда 
.(2)
Геометрически этот метод предлагает построить касательную к кривой y=f(x) в выбранной точке x=Zn, найти точку пересечения её с осью абсцисс и принять эту точку за очередное приближение к корню. Очевидно, что этот метод обеспечивает сходящийся процесс приближений лишь при выполнении некоторых условий (например при непрерывности и знакопостоянстве первой и второй производной функции в окрестности корня) и при их нарушении либо дает расходящийся процесс (4), либо приводит к другому корню. Очевидно, что для функций, производная от которых в окрестности корня близка к нулю, использовать метод Ньютона едва ли разумно. Если производная функции мало изменяется в окрестности корня, то можно использовать видоизменение метода.
17. Решить в пакете MATLAB уравнение с заданной точностью при заданном начальном приближении с использованием функции fzero.
Если xi и xi+1 расположенны близко друг к другу, то производная в выражении (2) можно заменить 
Тогда 
не требует вычисления производной.
В матлабе: x- начальное приближение корня
X=fzero(‘f(x)’,0.3,10^-5)
f(x)=0;x=ф(x) x+Ln(x)=0 x=-Ln(x)
вычисляем величину x1=ф(x0), x2=ф(x1), xn=ф(xn-1), если существ x*=LimXn, то этот предел есть корень уравнения.
18. Дано уравнение x=ф(x) 
. Показать, сходится или нет итерационный процесс Xn=ф(Xn-1) 
на заданном отрезке.
19. Дана система линейных алгебраических уравнений AX = B. Решить систему, используя средства MATLAB (не менее четырех способов решения).
| %ФАЙЛ ФУНКЦИЯ ДЛЯ ВЫЧИСЛЕНИЯ УРАВНЕНИЯ function X=f(a, b, eps) %Решение системы X=A*X+B методом простых итераций %eps-точность вычисления %k – количество итераций na=norm(a); delta=(1-na)/na*eps %Начальное приближение X0=b; X1=a*X0+b; k0=0; k1=k0+1; while norm(X1-X0)>delta X0=X1; X1=a*X0+b; k0=k1; k1=k0+1; end X=X1; k=k1 | %Первый способ привидения уравнения AX=B к виду, пригодному для решения %методом простых итераций. %Дана квадратная матрица A 4х4 и вектор-столбец B %A=[8 40 -3 0;-7 5 0 50;8 0 64 -11;32 0 0 5] %B=[28;0;18;12] format short A=[8 40 -3 0;-7 5 0 50;8 0 64 -11;32 0 0 5] B=[28;0;18;12] a=zeros(4,4);b=zeros(4,1); for i=1:4 b(i)=B(i)/A(i,i); a(i,i)=0 for j=1:4 if i~=j a(i,j)=-A(i,j)/A(i,i); end end end %Проверка условия norma (a)<1 mn=norm(a) me=norm(a,inf) %Вывод матрицы и вектора системы: a b %Решение уравнения format long e X=iter(alfa,beta, 10^-5) %Проверка disp('Погрешность') disp(norm(A*X-B)) | % Задаём матрицы format long e A=[8 40 -3 0;-7 5 0 50;8 0 64 -11;32 0 0 5] B=[28;0;18;12] % проверяем невырожденная ли матрица А DETERMINANT=det(A) % Решим систему уравнений % с использование обратной матрицы X1=(A^-1)*B %Проверка B1=A*X1 % с посмощью обращения матрицы X2=inv(A)*B %Провека B2=A*X2 % методом Гаусса с помощью правого деления X3=A\B %Проверка B3=A*X3 % методом Гаусса с помощью левого деления X4=B'/A' %Проверка B4=X4*A' | %Второй способ привидения уравнения AX=B к виду, пригодному для решения %методом простых итераций. %Дана квадратная матрица A 4х4 и вектор-столбец B format long e A=[8 40 -3 0;-7 5 0 50;8 0 64 -11;32 0 0 5] B=[28;0;18;12] d=[10^-5 10^-6 10^-4 10^-4; 10^-4 2*10^-7 10^-4 3*10^-4; 10^-7 10^-5 2*10^-4 3*10^-6; 3*10^-6 10^-8 2*10^-3 5*10^-4] alfa=d*A beta=(A^(-1)-d)*B %Проверка условия norm(alfa)<1 n_alfa=norm(alfa) format long e X=iter(alfa, beta, 10^-5) %проверка disp('погрешность') disp(norm(A*X-B)) |
20,21. Дан вектор. Вычислить m - норму вектора аналитически и в MATLAB (составить программу).
Даны вектор 
В матлабе: % Введём вектор b = [0 3 -4]; % Вычислим 1-норму вектора b norm(b, 1), % Вычислим 2-норму (евклидову) вектора b
norm(b), % Вычислим inf-норму вектора bnorm(b, inf)
21. Дан вектор. Вычислить l - норму вектора аналитически и в MATLAB (составить программу).
l- норма вектора: 
в Matlab n1=norm (X,1); Пример Дан вектор 
% Введём вектор
b = [0 3 -4];
% Вычислим l-норму вектора b
norm(b, 1)
>>
ans = 7
22,23. Дана матрица. Вычислить m - норму матрицы аналитически и используя встроенные в MATLAB средства.
единичная матрица 
В матлабе: 
22. Дана матрица. Вычислить m - норму матрицы аналитически и используя встроенные в MATLAB средства.
Max или m – норма: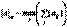 
в MatLab: nm=norm(A, inf); Пример 
% Введём матрицу
A = [-1 0 3;2 5 4; 7 10 -10];
% Вычислим inf-норму матрицы A
norm(A, inf)
>>
ans = 27
23. Дана матрица. Вычислить l - норму норму матрицы аналитически и используя встроенные в MATLAB средства.
L –норма 
в Matlab: nl=norm(A,1); Пример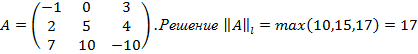 
% Введём матрицу
A = [-1 0 3;2 5 4; 7 10 -10];
% Вычислим l-норму матрицы A
norm(A, 1)
>>
ans = 17
24. Дана система линейных алгебраических уравнений X=aX+B 
. Проверить, что итерационный процесс сходится для m 
нормы. Определить условие окончания итерационного процесса.
AX=B, замена X=ax+b(9), a=[aij]I,j=1,n. b=[b1.b2.bn] Систему (9) решаем методом последовательных приближений. Если последовательность Xk имеет предел X*=LimXk, k->беск., то этот предел является решением. Если норма матрицы <1, то (9) имеет единственное решение и итерационный процесс сходится к решению независимо от начального приближения.
Пусть дано уравнение (1) AX=B Заменим его равносильным уравнением 
(9). Здесь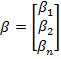 
, 
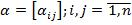Вычислительная формула метода простых итераций: 
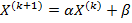(10). Если последовательность 
имеет предел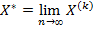 
, то этот предел является решением системы (10). Критерий окончания итерационного процесса: 
Пример: 
найдем с точностью 
. Приведем к виду удобному для итерации 
Выберем начальное приближение, например, 
- вектор правой части. Тогда первая итерация получается так:
Аналогично получаются следующие приближения к решению.
Найдем норму матрицы X. Будем использовать норму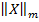 
. Так как сумма модулей элементов в каждой строке равна 0.2, то 
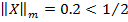, поэтому критерий окончания интераций в этой задаче 
. Вычислим нормы разностей векторов:
. Так как 
, заданная точность достигнута на четвертой итерации.
Ответ: x 1 = 1.102, x 2 = 0.991, x 3 = 1.101
25. Дана система линейных алгебраических уравнений AX = B. Привести ее к виду, пригодному для решения методом простых итераций X=aX+B . Проверить условие сходимости итерационного процесса для какой либо нормы.
В матрице A в каждой строке диагональный элемент по модулю больше суммы модулей остальных элементов строки. Если данное условие не выполняется, необходимо соответствующим образом преобразовать СЛАУ. Это можно сделать, выполнив эквивалентные преобразования системы(1):
Система уравнений.
Условие (1) не выполняется ни в одной из строк. Поместим строку (c) на первое место:.
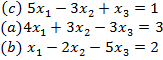
Теперь для первой и третьей строки условие (1) выполняется. В качестве третьей строки возьмем линейную комбинацию (c) – (a):
Далее:
Т.о.
, 
.
В качестве нулевого приближения примем 
.
В матлабе: файл сценарием задаем 2 матрицы А=[5 -3 1; 1 -6 4; 1 -2 5] и Б=[1;-2;2]. задаем а и б а=zeros(3,3);b=zeros(3,1);I,j=1,n;for i=1:3 b(i)= B(i)/A(I,j); a(I,i)=0; for j=1:3 if i~=j; a(I,j)=A(I,j)/A(I,i);endendend. % проверка условия ||a||<1. Nm=norm(a,inf),m1=norm(a,1),me=norm(a). a b.
26. Функция f(x) задана таблично на отрезке [a,b] . С какой точностью можно вычислить значение данной функции в указанной точке x1[a,b ] с помощью интерполяционного полинома Лагранжа.
f(x)= 
x=100,f(x)=10;x=144,f(x)=12; n=2
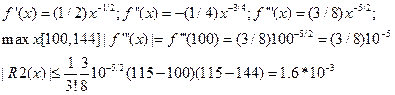
26. Функция f(x) задана таблично на отрезке [a, b] . С какой точностью можно вычислить значение данной функции в указанной точке 
с помощью интерполяционного полинома Лагранжа.
y=ln x на отрезке [1, 10]. Погрешность не меньше 10^-2
при линейной интерполяции
, так как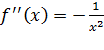 
, то 
. Тогда 
. Следовательно 
27. Функция f(x) задана таблично в точках x0 и x1 
. Построить интерполяционный полином Лагранжа L1(x)=ax+b . Создать M файл функцию L1(x) в MATLAB.
27. Функция f(a) задана таблично в точках 
и 
. Построить интерполяционный полином Лагранжа 
. Создать M- файл функцию 
в MATLAB.
| X | -1 | |||
| y |
% Введём табличную функцию
x = [-1 0 1 2];
y = [4 2 0 1];
% Построим интерполяционный многочлен (аппроксимация четвёртой степени)
p = polyfit(x, y, 4);
% Коэффициенты интерполяции \sum_{i=0}^n p(i) x^i
p
>>
| <== предыдущая лекция | | | следующая лекция ==> |
| Процедура визначення безпеки | | | ЗАТВЕДЖЕНО |