
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Пошук інформації
Дата добавления: 2015-08-17; просмотров: 715
|
|
Задание: Данные опыта представлены таблицей значений Х и У. Подобрать формулу эмпирической зависимости между Х и У. Найти параметры этой зависимости методом наименьших квадратов.
Вариант 1. Зависимость между нагрузкой У (кг) и сжатием X (мм)
буферной пружины:
| Х | ||||||
| У | 18,7 | 105,2 | 172,4 | 253,4 | 351,6 | 469,6 |
Вариант 2. Разрежение У (см. столба бензина) связано с расходом X топлива (см/мин).
| Х | 35,3 | 45,2 | 53,8 | 62,0 | 68,3 | 75,2 | 82,0 |
| У | 10,4 | 15,3 | 25,4 | 29,8 | 34,6 | 20,1 |
Вариант 3.Температура Х (С°) смазочного масла в двигателе связана с температурой У (С0 ) смазочного масла в коробке передач.
| Х | 33,7 | 34,5 | 37,0 | 38,0 | 39,0 | 39,3 | 35,5 |
| У | 22,1 | 24,0 | 24,4 | 26,0 | 25,8 | 22,4 | 25,8 |
Вариант 4. зависимость температур Х охлаждающегося тела от
времени Т.
| Х | |||||||
| У | 9,5 | 7,0 | 6,3 | 5,1 | 3,9 | 3,2 | 2,7 |
Вариант 5. Зависимость числа Х (об/мин) оборотов двигателя и мощности двигателя У (кВт)
| Х | |||||||
| У |
Вариант 6. Время непрерывной работы У (час) электроприборов зависит от расхода электроэнергии (кВт/сек)
| Х | 1,7 | 2,2 | 2,4 | 2,5 | 3,2 | ||
| У |
Вариант 7. Температура У (С0) смазочного масла в двигателе зависит от скорости Х (км/час) движения автомобиля.
| Х | 30,9 | 31,8 | 32,5 | 33,5 | 35,7 | 38,5 | 40,9 |
| У | 24,8 | 28,5 | 29,0 |
Вариант 8. Износ лемеха У (мм) зависит от твердости Х (нрс) материала лемеха.
| Х | |||||
| У | 0,7 | 0,9 | 0,9 | 1,1 | 0,8 |
Вариант 9.Мощность двигателя У (кВт) связана с температурой Х (С0) воздуха.
| Х | 30,9 | 31,8 | 32,5 | 33,5 | 35,7 | 38,5 | 40,9 |
| У | 24,8 | 28,5 | 29,0 |
Вариант 10.Вибрация У автомобиля зависит от скорости Х (км/час) движения.
| Х | |||||
| У |
Вариант 11.Прогиб балки У (м) связана с нагрузкой Х (кН).
| Х | ||||||
| у |
Вариант 12. Электрические сопротивление R (Ом) проволоки зависит от температуры t (С0).
| t | 20.0 | 24.8 | 30.2 | 35.0 | 40.1 | 44.9 | 50.0 |
| R | 86.7 | 88.03 | 90.32 | 91.15 | 93.26 | 94.9 | 96.33 |
Вариант 13. Дана таблица удельного сопротивления (кн/м2) и производительности У (га/ч) посевного агрегата..
| Х | |||||
| у |
Вариант 14. Результаты измерений длительности Х (час) непрерывной работы двигателя и расхода У (л) топлива задана следующей таблицей.
| Х | 10,5 | ||||
| у | 22,5 | 21,5 | 21,5 |
Вариант 15. Скорость У охлаждения тела зависит от разности Х температуры и окружающей среды.
| Х | |||||
| у |
| х | |||||||
| У | 8,81 | 7,4 | 6,1 | 4,89 | 3,88 | 3,02 | 2,3 |
Вариант 16. Известны твердость Х ( кг/см2) почвы и износ У (мм) лемеха.
Вариант 17. Крутящий момент У (кг/см) зависит от угла кручения Х (рад).
| Х | |||||
| у | 10,4 | 12,53 | 15,41 | 19,2 | 23,67 |
Вариант 18. Стационарное распределение температуры в теплоизолированном тонком стержне задано таблицей значений измеренных температур У в соответствующих точках Х.
| Х | ||||||||
| у | 29,2 | 23,3 | 19,9 | 17,2 | 11,3 | 7,82 |
Вариант 19. Показатели скорости движения Х (км/час) и износа У (мм) лемеха следующие:
| Х | ||||||
| у |
Вариант 20. Дана зависимость электрического сопротивления R (Ом) проводника от температуры t (с0).
| t | 19.1 | 30.1 | 36.0 | 45.1 | 50.0 | ||
| R | 76.3 | 77.8 | 79.75 | 80.8 | 82.35 | 83.9 | 85.1 |
Вариант 21. Известны износ Х поршневых колец и расход У топлива.
| Х | ||||||
| У |
Вариант 22. Известны твердость Х и стойкость У сверл.
| Х | ||||||
| У |
Вариант 23. Известны Х- стрела кривизны рельса (см), а У- количество дефектов рельса (см).
| Х | 9,0 | 9,5 | 10,5 | 11,5 | |||
| У |
Вариант 24.Известны Х – срок службы колеса вагона в годах, У-усредненное значение износа по толщине обода колеса.
| Х | |||||||
| У |
Вариант 25. Известны Х- процентное отношение предела текучести к прочности стали; У- процентное содержание углерода в стали.
| Х | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
| У | 0,6 | 0,8 | 0,7 | 0,5 | 0,5 |
Контрольные вопросы:
1. Какие формулы называются эмпирическими?
2. Из каких этапов состоит процесс нахождения эмпирических формул?
3. Как выбрать вид функциональной зависимости?
4. В чем суть метода наименьших квадратов?
5. Как вычислить отклонение?
6. Сформулировать необходимый признак экстремума функции двух переменных.
7. Какой вид имеет нормальная система метода наименьших квадратов в случае линейной зависимости и квадратичной?
8. Вывести нормальную систему в случае линейной зависимости.
9. Вывести нормальную систему в случае квадратичной зависимости.
10. Каким методом можно решать систему уравнений?
11. Как получить искомую эмпирическую функцию?
12. Как составляется расчетная таблица в случае линейной зависимости?
13. Какие расчетные данные нужно добавить в таблицу 3 § 2 в случае квадратичной зависимости?
14. Составить алгоритмы решения системы уравнения по правилу Крамера и Гаусса.
Литература:
1. Вопросы статистики Москва 2004.
2. Гатаулин А.М. Харитонова Л.А. Нефедова Э.С. Математика для сельского экономиста, М. Россельхозиздат, 1975.
3. Доспехов Б.А. Методика опытного поля, М. Агропромиздат, 1985.
4. Дипачев В.С. Высшая математика, М. Высшая школа, 1985.
5. Иванова О.А. Генетика, М. колос 1974.
6. Королев Ю.Г. Метод наименьших квадратов в социально-экономических исследованиях. М.Статистика 1980
7. Кассандрова О.Н. Лебедев В.В. обработка результатов наблюдений, М. Наука 1970.
8. Лихолетов И.И. высшая математика, теория вероятности и математическая статистика, Минск. Высшая школа 1976.
9. Львовский Е.Е. Статистические методы построения эмпирических формул, М. Высшая школа 1982.
10. Соломенко Л.К. Биометрия. Пособие к практикуму для студентов – заочников зоотехнического факультета. М.1971.
11. Плис А.И. Сливина Н.А. Лабораторный практикум по высшей математике, М. Высшее образование 1983.
12. Пискунов Н.С Дифференциальное и интегральное исчисление, Т.1, м. Наука 1972.
Содержание:
Предисловие …………………………………………………………….. 3
§ 1. Краткая теория
1.1 Постановка задачи ………………………………………….…. 4
1.2 Выравнивание по прямой ……………………………………... 5
1.3 Выравнивание по параболе…………………………………...…7
§ 2. Порядок выполнения задания ………………………………………. 9
§ 3. Образец выполнения задания ……………………………………… 10
3.1. Замечание. Метод наименьших квадратов в обработке рядов динамики. ………………………………………………………………… 15
§ 4. Варианты для самостоятельной работы.
4.1. Задания для студентов экономического факультета ………….17
4.2. Задания для студентов агро-технологического института и института биотехнологий и ветеринарной медицины ……………….. 20
4.3. Задания для студентов механико-технологического института …………………………………………………………….......................... 24
§ 5. Контрольные вопросы ………………………………………..... 29
Литература ……………………………………………………………30
Методическая разработка
для студентов фармацевтического факультета
к практическому занятию по теме:
«Метод наименьших квадратов. Сглаживание экспериментальных зависимостей»
1. Научно-методическое обоснование темы:
Задача сглаживания экспериментальных зависимостей достаточно типична для практики. При ее решении рассчитывают освободить экспериментальные данные от случайных ошибок, допущенных в каждом отдельном опыте, и свести большое количество этих данных к нескольким параметрам (в част
ности, к коэффициентам многочлена), одновременно получив возможность обрабатывать полученную функциональную зависимость аналитически (например, дифференцировать).
2. Краткая теория:
Предположим, что результаты некоторого эксперимента систематизированы в виде таблицы,
Таблица 1

в которой yi = y(xi ) является функцией, а х — аргументом, и требуется сгладить эту заданную таблично зависимость многочленом или некоторой другой функцией, известной нам с точностью до нескольких подлежащих определению параметров.
Практически любая табличная зависимость может быть сглажена различными функциями с приблизительно одинаковой точностью. Сглаживающую функцию следует выбирать исходя из физических соображений, а при отсутствии таковых использовать наиболее простые варианты формул, с минимальным числом подлежащих определению коэффициентов. Определенную помощь в выборе сглаживающей функции может также оказать графическое представление табл. 1. (рис.1).
Пусть, для определенности, сглаживающая функция является многочленом
 , (1)
, (1)

Рис.1 Графическое представление табл.1
известной степени  с числовыми коэффициентами
с числовыми коэффициентами  которые подлежат определению.
которые подлежат определению.
Составим разности
 (2)
(2)
характеризующие близость табличных данных и значений, полученных при помощи сглаживающей функции. Подберем коэффициенты  таким образом, чтобы величины
таким образом, чтобы величины  в совокупности были минимальными.
в совокупности были минимальными.
Эффективной процедурой для решения подобного рода задач является так называемый метод наименьших квадратов, который гласит, что наилучшими во многих отношениях оценками для  являются оценки, минимизирующие сумму квадратов разностей
являются оценки, минимизирующие сумму квадратов разностей  . Другими словами, в качестве оценки для неизвестных параметров αi следует взять такие значения ai, при которых функция
. Другими словами, в качестве оценки для неизвестных параметров αi следует взять такие значения ai, при которых функция

достигает минимума. Так как  представляет дифференцируемую функцию r переменных, необходимым условием ее минимизации является равенство нулю частных производных
представляет дифференцируемую функцию r переменных, необходимым условием ее минимизации является равенство нулю частных производных  , вычисленных при
, вычисленных при 

Решение системы из r + 1 нормального уравнения
 , (3)
, (3)
дает искомые коэффициенты  Рассмотрим более детально линейную аппроксимацию экспериментальных зависимостей между величинами, т. е. сглаживание с помощью функции
Рассмотрим более детально линейную аппроксимацию экспериментальных зависимостей между величинами, т. е. сглаживание с помощью функции  В этом случае
В этом случае

и система нормальных уравнений принимает вид
 (4)
(4)
Пусть
 , (5)
, (5)
Тогда систему (4) можно переписать в виде
 , (6)
, (6)
Решая систему двух линейных уравнений с двумя неизвестными (6), получим
 , (7)
, (7)
Таким образом, наилучшая в смысле метода наименьших квадратов линейная сглаживающая функция выражается уравнением 
Замечание 1. Сумма  оптимальных разностей равняется нулю. Это можно использовать для контроля правильности вычислений.
оптимальных разностей равняется нулю. Это можно использовать для контроля правильности вычислений.
Пример 1. Сгладить линейной зависимостью от х данные, представленные в таблице
Таблица 2

Вычислить разности и отобразить на графике табличные данные и сглаживающую прямую.
Решение. Используя формулы (5) найдем


и, следовательно,
 .
.
Таким образом, уравнение сглаживающей прямой имеет вид у = 2 + 0,36x (рис. 2).

Рис.2. График сглаживающей прямой
Теперь дополним табл. 2:
Таблица 3

Как видно из табл.3. сумма разностей равна нулю.
Замечание 2. Метод наименьших квадратов можно с некоторой потерей точности использовать для сглаживания функциональных зависимостей, приводящихся к линейной с помощью замены переменных. Так, зависимость  может быть переписана в виде
может быть переписана в виде  Применяя метод наименьших квадратов для нахождения коэффициентов линейного уравнения
Применяя метод наименьших квадратов для нахождения коэффициентов линейного уравнения  и возвращаясь к первоначальной зависимости, получим в качестве оценки коэффициента
и возвращаясь к первоначальной зависимости, получим в качестве оценки коэффициента  величину
величину 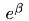 (оценка для
(оценка для  в данном случае остается без изменений).
в данном случае остается без изменений).
Пример 2. Данные измерений некоторой физической величины представлены таблицей:
Таблица 4

Сгладить эти данные при помощи формулы  и вычислить разности между табличными и сглаженными значениями с точностью до тысячных.
и вычислить разности между табличными и сглаженными значениями с точностью до тысячных.
Решение. Воспользуемся замечанием 2:
1) Заменим числа z из табл. 4 числами у = lnz:
Таблица 5

2) По формулам (5) и (7) найдем коэффициенты ао = 0,6876 и ах = 0,1006 линейного уравнения ao+a1x , наилучшим образом приближающего у.
3) Учитывая, что коэффициенты αо и α1 связаны с ао и а1 соотношениями  окончательно получим αо = 1,988, α1 = 0,1006, и, следовательно,
окончательно получим αо = 1,988, α1 = 0,1006, и, следовательно,  .
.
Разности между табличными и сглаженными значениями z сведем в таблицу:
Таблица 6

Как видно из табл.6, сумма разностей здесь отлична от нуля.
3. Цель деятельности студентов на занятии:
Студент должен знать:
1. Цели сглаживания экспериментальных зависимостей.
2. Метод наименьших квадратов.
Студент должен уметь:
Применять метод наименьших квадратов для сглаживания экспериментальных зависимостей.
4. Содержание обучения:
Теоретическая часть:
1. Задача сглаживания экспериментальных зависимостей.
2. Выбор сглаживающей функции.
3. Метод наименьших квадратов.
4. Линейная аппроксимация экспериментальных зависимостей.
Практическая часть:
Используя метод наименьших квадратов, сгладить с помощью функций заданного вида следующие табличные зависимости:

5.Перечень вопросов для проверки исходного уровня знаний:
1. С какой целью проводится сглаживание экспериментальных зависимостей между величинами?
2. Из каких соображений следует выбирать сглаживающую функцию?
3. В чем заключается метод наименьших квадратов?
6. Перечень вопросов для проверки конечного уровня знаний:
1. Как проводится сглаживание с помощью линейной функции?
2. Приведите формулы для коэффициентов уравнения при линейной аппроксимации экспериментальных зависимостей.
3. Как используют метод наименьших квадратов для сглаживания функциональных зависимостей , приводящихся заменой переменных к линейному виду?
7. Хронокарта учебного занятия:
1. Организационный момент – 5 мин.
2. Разбор темы – 20 мин.
3.Решение ситуационных задач - 40 мин.
4. Текущий контроль знаний -30 мин.
5. Подведение итогов занятия – 5 мин.
8. Перечень учебной литературы к занятию:
Павлушков И.В. и др. Основы высшей математики и математической статистики. М., «ГЭОТАР-Медиа», 2006, § 8.3.
| <== предыдущая лекция | | | следующая лекция ==> |
| Тема 1.2 Алгоритм прийняття рішення про покупку | | | Оцінка варіантів |