ПР НАВИЧКИ КРОВООБІГ

Дата добавления: 2015-08-17; просмотров: 556

[2] гл. XIV, XV; [3] № 1598, 1607, 1612, 1619, 1622, 1629, 1636, 1670, 1686.

Разберите решение задачи 11 данного пособия.

Задача 11. Вычислить площадь фигуры, ограниченной ли­ниямиу=х²+4х, у=х+4 (рис. 8).

Решение. Площадь S фигуры, ограниченной сверху и снизу непрерывными линиямиу=f(х) иу= 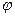(х), пересекаю­щимися в точках с абсциссамих=а их=b, определяется по формуле

S= (1)

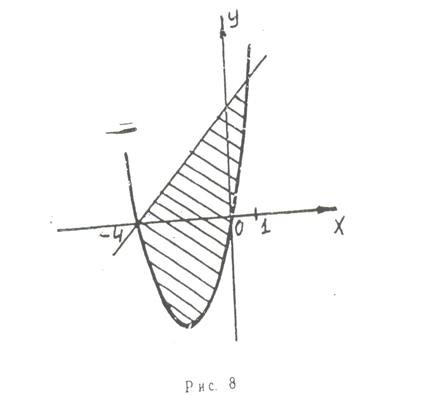
Для нахождения точек пересечения данных линий решаем систему уравнений

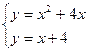
х 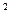+4х=х+4, х 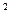+3х-4=0, откуда х =-4, х =1.

Применяя формулу (1), получим:

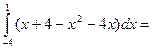
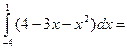
S= (кв.ед.).

Вопросы для самопроверки

1. Назовите задачи, приводящие к понятию определенно­го интеграла.
2. Напишите интегральную сумму для функции у =f (х) на отрезке [а;b].
3. Что называется определенным интегралом от функции у =f(х) на отрезке [а;b].
4. Каков геометрический смысл определенного инте­грала?
5. Перечислите основные свойства определенного интеграла.
6. Чему равна производная от определенного интеграла с переменным верхним пределом интегрирования?
7. Напишите формулу Ньютона—Лейбница.
8. Напишите формулу интегрирования по частям в опре­деленном интеграле.
9. Как вычислить объем тела, образованного вращением плоской фигуры вокруг осиОх? оси Оу?
10. Дайте определение несобственного интеграла с беско­нечными пределами интегрирования.
11. Сформулируйте понятие несобственного интеграла от разрывной функции.