
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
ДИХАННЯ ТЕСТИ З БАЗИ ЛИШЕ З ПРАВИЛЬНИМИ ВІДПОВІДЯМИ
Дата добавления: 2015-08-17; просмотров: 688
|
|
[2] гл. XXII § 1—13; [3] № 2058, 2067, 2094, 2102, 2165, 2186,2213,2215,
Разберите решение задач 12, 13 данного пособия.
Задача 12. Решить уравнениеу'—уtgх =-у2соз х.
Решение. Данное уравнение является уравнением Бернулли. Для его решения (как и для линейного уравнения) искомую функцию у представим в виде произведения двух других функций:и=и(х) и  =
=  (x), то есть введем подстановку у=и*
(x), то есть введем подстановку у=и*  . Тогдау'=и'
. Тогдау'=и'  +и
+и  ' и данное уравнение примет вид:
' и данное уравнение примет вид:
и'  + и
+ и  '- и
'- и  tg х= -
tg х= -  .
.
или
 (и'-иtgх)+и
(и'-иtgх)+и  '=-
'=-  . (1)
. (1)
Выберем функцию и так, чтобы
и'-иtgх=0. (2)
При подобном выборе функции и уравнение (1) примет вид
и  '=-
'=-  или
или  '=-
'=-  . (3)
. (3)
Решая (2) как уравнение с разделяющимися переменными, имеем:
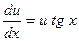 ,
,  , In и = - In cos х, и=-
, In и = - In cos х, и=-  .
.
Здесь произвольная постоянная С=0. Подставляя найденное значение и в уравнение (3) , имеем:
 ,
, 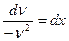 ,
,  ,
, 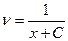 .
.
Тогда у=и*  =
=  - общее решение данного уравнения.
- общее решение данного уравнения.
Задача 13. Найти частное решение уравненияу"+4у=4sin2х-8cos2х, удовлетворяющее начальным условиям у(0)=0, у' (0) =0.
Решение. Общее решение у данного уравнения равно сумме общего решения у  однородного уравнения и какого-либо частного решения у данного уравнения, то есть
однородного уравнения и какого-либо частного решения у данного уравнения, то есть
у= у  +
+ 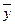 .
.
Для нахожденияу  составим характеристическое уравнение R
составим характеристическое уравнение R 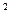 +4=0, имеющее комплексные корни.
+4=0, имеющее комплексные корни.
R  =2i и R
=2i и R  =-2i. В этом случае общее решение однородного уравнения ищем в виде
=-2i. В этом случае общее решение однородного уравнения ищем в виде
у  = е
= е  (С
(С  cos
cos 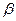 х+С
х+С  sin
sin 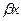 ), (4)
), (4)
где  — комплексные корни характеристического уравнения. Подставив в (4)
— комплексные корни характеристического уравнения. Подставив в (4)  =0,
=0, 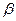 = 2, имеем:
= 2, имеем:
у  =C
=C  cos2х+С
cos2х+С  sin2х.
sin2х.
Для нахождения частного решения 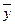 неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция f(х)= е
неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция f(х)= е  (аcos
(аcos 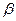 х+bsin
х+bsin 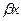 ) и числа
) и числа  не являются корнями характеристического уравнения, то существует частное решение
не являются корнями характеристического уравнения, то существует частное решение
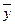 = е
= е  (Аcos
(Аcos 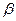 х+Вsin
х+Вsin 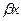 ). Если же числа
). Если же числа  являются корнями характеристического уравнения, то существует частное решение
являются корнями характеристического уравнения, то существует частное решение
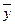 = хе
= хе  (Аcos
(Аcos 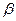 х+Вsin
х+Вsin 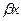 ).
).
Применяя эту теорему при  ,
, 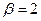 , имеем:
, имеем:
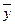 = х (Аcos2х+Вsin2х).
= х (Аcos2х+Вsin2х).
Дважды дифференцируя последнее равенство, находим  =(4В-4Ах)cos2х+(-4А-4Вх)sin2х.
=(4В-4Ах)cos2х+(-4А-4Вх)sin2х.
Подставив в данное уравнение 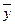 и
и  получим:
получим:
4Всоз2х—4Аsin2х=4sin2х-8соз2х,
откудаА =-1, В = —2.
Следовательно, 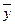 =-х(cos2х+2sin2х) и у= C
=-х(cos2х+2sin2х) и у= C  cos2х+С
cos2х+С  sin2х-х(cos2х+2sin2х).
sin2х-х(cos2х+2sin2х).
Найдем у':
у'=-2 sin2х+2С  cos2х- cos2х-2 sin2х-х(-2 sin2х+4 cos2х).
cos2х- cos2х-2 sin2х-х(-2 sin2х+4 cos2х).
Используя начальные условия, получим систему
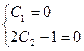 , откуда C
, откуда C  =0, С
=0, С  =
= 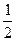 .
.
Следовательно,
у= 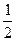 sin2х-х(cos2х+2sin2х) - есть искомое частное решение данного дифференциального уравнения.
sin2х-х(cos2х+2sin2х) - есть искомое частное решение данного дифференциального уравнения.
Вопросы для самопроверки
12. Что называется дифференциальным уравнением?
13. Что называется общим решением дифференциального уравнения? частным решением?
14. Каков геометрический смысл частного решения дифференциального уравнения первого порядка?
15. Приведите примеры дифференциальных уравнений с разделяющимися переменными.
16. Какое дифференциальное уравнение первого порядка называется линейным? уравнением Бернулли? Укажите способ их решения.
17. Какое уравнение называется линейным дифференциальным уравнением второго порядка?
18. Какое уравнение называется характеристическим для однородного дифференциального уравнения второго порядка?
19. Какой вид имеет общее решение однородного дифференциального уравнения второго порядка в зависимости от дискриминанта характеристического уравнения?
20. Как найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами?
21. Какой вид имеет частное решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его правая часть есть многочлен? показательная функция? тригонометрическая функция?
| <== предыдущая лекция | | | следующая лекция ==> |
| ПР НАВИЧКИ КРОВООБІГ | | | ТЕРМОРЕГУЛЯЦІЯ |