Moving Heavy Oil

Дата добавления: 2015-08-27; просмотров: 543

Ставка процентов – величина, характеризующая интенсивность начисления процентов.

Наращение первоначальной суммы долга – увеличение суммы долга за счет присоединения начисленных процентов и доходов.

Множитель наращения – величина, показывающая во сколько раз возрос первоначальный капитал.

Период начисления – промежуток времени, за который начисляются проценты.

Интервал начисления – минимальный период, по прошествии которого происходит начисление процентов.

Существуют два способа начисления процентов.

Декурсивный способ – проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из величины предоставляемого капитала. Декурсивная процентная ставка представляет собой сумму начисленного за определенный интервал дохода к сумме, имеющейся в начале интервала, в процентном отношении.

Антисипативный (предварительный) способ – проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращения суммы. Процентной ставкой будет выраженное в процентах отношение суммы дохода за интервал к величине наращенной суммы, полученной по прошествии этого интервала. Такая процентная ставка называется учетной.

Простые ставкиприменяются к одной и той же первоначальной денежной сумме в течение всего периода начисления. При декурсивном способе простые ставки применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления и составляет срок менее одного года, или когда после каждого интервала кредитору выплачиваются проценты.

Если обозначить будущую сумму S, а современную (или первоначальную) P, то I = S – P (1). Процентная ставка i является относительной величиной, измеряется в десятичных дробях или %, и определяется делением процентов на первоначальную сумму: i=I/P

Кроме процентной существует учетная ставка d (другое название – ставка дисконта), величина которой определяется по формуле:

S-P=D, P=S 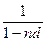(2)

где D – сумма дисконта.

Однако продолжительность ссуды (или другой финансовой операции, связанной с начислением процентов) n необязательно должна равняться году или целому числу лет. Если обозначить продолжительность года в днях буквой K (этот показатель называется временная база), а количество дней пользования ссудой t, то использованное в формулах (3) и (4) обозначение количества полных лет n можно будет выразить как t/K. Подставив это выражение в (1) и (2), получим:

для декурсивных процентов: S=P(1+ i) (3)

для антисипативных процентов: S=P (4)

Если после очередного интервала начисления доход не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяется формула сложных процентов.

Сложные ставки процентов учитывают возможность реинвестирования процентов, так как в этом случае наращение производится по формуле не арифметической, а геометрической прогрессии, первым членом которой является начальная сумма P, а знаменатель равен (1 + i).

P, P * (1 + i), P * (1 + i)², P * (1 + i)³ , …, P * (1 + i)ⁿ,

где число лет ссуды n меньше числа членов прогрессии k на 1 (n = k – 1).

Наращенная стоимость (последний член прогрессии) находится по формуле:

S=P*(1+I) (5)

где (1 + i) ⁿ – множитель наращения декурсивных сложных процентов.

Так же как и в случае простых процентов возможно применение сложной учетной ставки для начисления процентов (антисипативный метод):

S=P* 1/(1-d)^n (6)

где 1/(1 – d)^n – множитель наращения сложных антисипативных процентов.

Формула наращения по сложным процентам при начислении их m раз в году имеет вид:

S=P*(1+ )^m*n (7)

При начислении антисипативных сложных процентов, номинальная учетная ставка обозначается буквой f, а формула наращения принимает вид:

S= (8)

Наиболее щепетильные кредиторы, принимая во внимание большую эффективность простых процентов на коротких отрезках времени, используют смешанный порядок начисления процентов в случае, когда срок операции (ссуды) не равен целому числу лет: сложные проценты начисляются на период, измеренный целыми годами, а проценты за дробную часть срока начисляются по простой процентной ставке.

S=P*(1+i)^a+ (9)

Непрерывная процентная ставка (очевидно, что при непрерывном начислении речь может идти только о сложных процентах) обозначается буквой δ (читается «дельта»), часто этот показатель называют «сила роста». Формула наращения по непрерывной процентной ставке имеет вид:

S=P*e^δn (10)

где e – основание натурального логарифма (≈2,71828...),

e^n – множитель наращения непрерывных процентов.

Существует несколько правил, позволяющих быстро рассчитать срок удвоения первоначальной суммы для каждой конкретной процентной ставки.

Правило «72»:

n = 72 / i %.

Правило «69»:

n = (69 / i %) + 0,35.

Данные правила дают достаточно точный результат при небольших значениях i, т.е. до i% = 100%.

Финансовые потоки, формируемые под воздействием изменения стоимости денег во времени, имееют свои закономерности и тягу к упорядоченности. В финансовом анализе для обозначения денежных потоков в наиболее общем смысле используется термин рента. Каждый отдельный рентный платеж называют членом ренты. Частным случаем ренты является финансовая рента или аннуитет – такой поток платежей, все члены которого равны друг другу, так же как и интервалы времени между ними.

Рекомендуемая литература:

1. Беренс В., Хавранек П.М. Руководство по оценке эффективности инвестиций. – М.: АОЗТ «Интерэксперт»; «ИНФРА - М», 1995

2. Бригхем Ю., Гапенски Л. Финансовый менеджмент (т. 1, 2). – СПб.: Экономическая школа, 1998

3. Криничанский К. Финансовая математика. Учебное пособие. – М.: «Дело и Сервис», 2011. – 336 с.

4. Печенежская И. Финансовая математика: сборник задач. – М.: Феникс, 2008. – 188 с.

5. Четыркин Е.М. Финансовая математика. – М.: «Дело и Сервис», 2011. – 392 с.

Примеры решения задач: