
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
ПРОТОКОЛ
Дата добавления: 2015-08-27; просмотров: 634
|
|
Чаще всего информация представляется в виде языковых сообщений (цепочек знаков или слов), причем в процессе ее обработки форма представления может меняться. Например, сообщение, предназначенное для передачи по телеграфу, первоначально может быть представлено в виде рукописного текста. Телеграфист переводит это сообщение в последовательность длинных, коротких импульсов и пауз, передающихся по телеграфному каналу. А на приемном конце такая последовательность может быть преобразована в печатный текст. Рассмотренные преобразования представляют собой пример кодирования сообщений. Еще одним примером кодирования является тайнопись, когда исходное сообщение преобразуется в другую форму, скрывающую содержание исходного сообщения.
Различные задачи кодирования можно формализовать следующим образом. Пусть 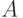 и
и 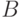 алфавиты,
алфавиты, 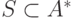 некоторое множество слов в алфавите
некоторое множество слов в алфавите 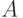 . Тогда функция
. Тогда функция
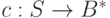
называется кодированием или кодом. Кодом называется также образ отображения  , обозначаемый
, обозначаемый 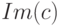 . Если существуетобратная функция
. Если существуетобратная функция 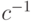 , то она называется декодированием. Одно и то же множество сообщений можно закодировать многими различными способами. Поэтому среди многих вариантов кодирования ищут такой, который был бы оптимальным в некотором смысле или обладал определенными полезными свойствами. Наиболее естественным требованием является возможность декодирования.
, то она называется декодированием. Одно и то же множество сообщений можно закодировать многими различными способами. Поэтому среди многих вариантов кодирования ищут такой, который был бы оптимальным в некотором смысле или обладал определенными полезными свойствами. Наиболее естественным требованием является возможность декодирования.
Побуквенное (алфавитное) кодирование. Обычно, кодирование множества слов 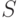 производится с помощью функции кодирующей отдельные буквы алфавита
производится с помощью функции кодирующей отдельные буквы алфавита 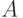 . Для этого случая определение кода будет следующим.
. Для этого случая определение кода будет следующим.
Кодом называется отображение
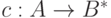
| ( 6.2) |
сопоставляющее каждому знаку из алфавита 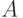 некоторое слово, которое составлено из знаков, входящих в
некоторое слово, которое составлено из знаков, входящих в 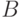 . Слова, входящие в
. Слова, входящие в 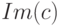 , называются кодовыми словами. Отображение (6.2) может задаваться любым из известных в математике способов. Для конечного множества
, называются кодовыми словами. Отображение (6.2) может задаваться любым из известных в математике способов. Для конечного множества 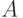 чаще всего используется табличный способ, задающий код (6.2) таблицей.
чаще всего используется табличный способ, задающий код (6.2) таблицей.
| Кодируемая буква алфавита А | Кодовое слово |
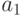
| 
|
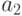
| 
|

| 
|
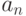
| 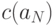
|
Такая таблица называется кодовой таблицей. В качестве примера можно привести таблицу кодирования алфавита  из цифр восьмеричной системы счисления словами из упоминавшегося ранее бинарного алфавита
из цифр восьмеричной системы счисления словами из упоминавшегося ранее бинарного алфавита 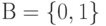 . В данном случае отображение (6.2) имеет вид
. В данном случае отображение (6.2) имеет вид 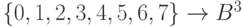 .
.
| Кодируемый знак | Кодовое слово |
Еще одним примером является так называемый код ASCII, фрагмент которого показан в следующей таблице.
| Знак | Кодовое слово (в десятичной системе счисления) | Кодовое слово (в шестнадцатеричной системе счисления) |
| … | … | |
| a | ||
| b | ||
| c | ||
| d | ||
| e | ||
| f | ||
| g | ||
| h | ||
| i | ||
| j | 6A | |
| … | … |
Кодирование слов. Отображение (6.2) позволяет перейти от кодирования отдельных знаков (букв конечного алфавита) к кодированию слов. Если 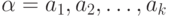 - слово, состоящее из знаков (полученное конкатенацией знаков)
- слово, состоящее из знаков (полученное конкатенацией знаков) 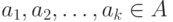 , то кодом
, то кодом 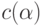 слова
слова  (по определению) является конкатенация кодов
(по определению) является конкатенация кодов 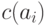 знаков
знаков 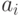 , образующих слово, т. е.
, образующих слово, т. е. 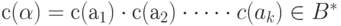 . Например, с применением таблицы ASCII кода (см. последнюю таблицу) слово head будет закодировано последовательностью 10410197100 при использовании десятичной системы счисления или последовательностью 68656164 - в шестнадцатеричной.
. Например, с применением таблицы ASCII кода (см. последнюю таблицу) слово head будет закодировано последовательностью 10410197100 при использовании десятичной системы счисления или последовательностью 68656164 - в шестнадцатеричной.
Условие (необходимое) однозначной декодируемости заключается в инъективности отображения (6.2). Инъективность обеспечивает однозначную декодируемость отдельных знаков из алфавита 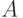 . Однако однозначной декодируемости слов из
. Однако однозначной декодируемости слов из 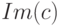 это условие не обеспечивает, если коды отдельных знаков, входящих в слово, следуют один за другим и не разделяются специальным символом. Подробнее проблема однозначной декодируемости будет рассмотрена позже.
это условие не обеспечивает, если коды отдельных знаков, входящих в слово, следуют один за другим и не разделяются специальным символом. Подробнее проблема однозначной декодируемости будет рассмотрена позже.
В частном случае, когда знаки из 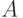 кодируются однобуквенными словами, отображение (6.2) имеет вид
кодируются однобуквенными словами, отображение (6.2) имеет вид 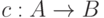 и представляет собой простую замену (подстановку) знаков. Однако чаще всего, в основном из-за использования в большинстве технических устройств обработки информации двоичного алфавита
и представляет собой простую замену (подстановку) знаков. Однако чаще всего, в основном из-за использования в большинстве технических устройств обработки информации двоичного алфавита 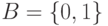 , каждый знак из
, каждый знак из 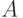 кодируется последовательностью знаков (словом) из B.
кодируется последовательностью знаков (словом) из B.
Недостаточность количества знаков в алфавите 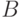 является препятствием применения простой замены для кодирования (не обеспечивается инъективность и, следовательно, однозначность декодируемости при
является препятствием применения простой замены для кодирования (не обеспечивается инъективность и, следовательно, однозначность декодируемости при 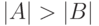 ). Для устранения этой проблемы используются множества новых, "составных" объектов из степеней
). Для устранения этой проблемы используются множества новых, "составных" объектов из степеней  алфавита
алфавита 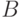 . Множество
. Множество 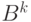 состоит из упорядоченных последовательностей элементов из
состоит из упорядоченных последовательностей элементов из 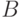 (векторов) длины
(векторов) длины 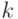 . Число элементов
. Число элементов 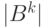 множества
множества 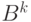 равно
равно 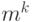 . Например, для двоичного алфавита
. Например, для двоичного алфавита 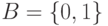 имеем
имеем 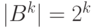 . Таким образом, взяв достаточно большую степень
. Таким образом, взяв достаточно большую степень 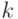 , можно получить нужное количество элементов вторичного алфавита.
, можно получить нужное количество элементов вторичного алфавита.
Если каждый знак алфавита 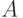 отображается при кодировании
отображается при кодировании 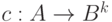 в слово одинаковой длины
в слово одинаковой длины 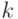 , то говорят, что код является кодом постоянной длины. Такие коды широко распространены, поскольку для обработки сообщений используются вычислительные машины, коммуникацион-ные устройства и другое оборудование, имеющее регистры фиксированного размера.
, то говорят, что код является кодом постоянной длины. Такие коды широко распространены, поскольку для обработки сообщений используются вычислительные машины, коммуникацион-ные устройства и другое оборудование, имеющее регистры фиксированного размера.
Процедуру кодирования слова 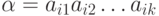 в алфавите
в алфавите 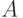 можно представить следующим образом. Имеется кодовая таблица, в левом столбце которой находятся кодируемые буквы алфавита
можно представить следующим образом. Имеется кодовая таблица, в левом столбце которой находятся кодируемые буквы алфавита 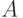 , а в правом столбце - соответствующие кодовые слова (кодовые слова могут иметь различную длину).
, а в правом столбце - соответствующие кодовые слова (кодовые слова могут иметь различную длину).
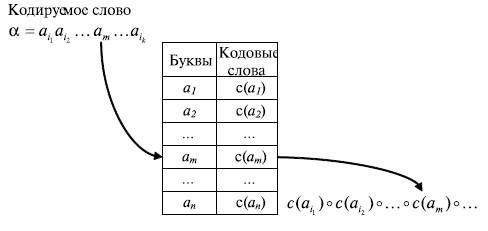
Рис. 6.4. Процедура кодировании слов с использованием кодовой таблицы
Для каждого знака слова 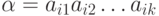 , начиная с первого знака, в кодовой таблице находится строка, в которой в левом поле располагается кодируемый знак (буква), и из правого поля этой строки берется соответствующее кодовое слово в алфавите
, начиная с первого знака, в кодовой таблице находится строка, в которой в левом поле располагается кодируемый знак (буква), и из правого поля этой строки берется соответствующее кодовое слово в алфавите 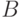 . Найденное кодовое слово приписывается слева (конкатенируется) к уже сформированной части кода слова
. Найденное кодовое слово приписывается слева (конкатенируется) к уже сформированной части кода слова  . Кодовое слово первой буквы слова
. Кодовое слово первой буквы слова  приписывается к пустому слову е. Эта процедура схематически показана на рис.6.4.
приписывается к пустому слову е. Эта процедура схематически показана на рис.6.4.
30. Оптимальное кодирование, свойства оптимальных кодов, построение оптимального кода методом Хафмена. Сжатие данных.
Кодирование Хаффмана является простым алгоритмом для построения кодов переменной длины, имеющих минимальную среднюю длину. Этот весьма популярный алгоритм служит основой многих компьютерных программ сжатия текстовой и графической информации. Некоторые из них используют непосредственно алгоритм Хаффмана, а другие берут его в качестве одной из ступеней многоуровневого процесса сжатия. Метод Хаффмана [Huffman 52] производит идеальное сжатие (то есть, сжимает данные до их энтропии), если вероятности символов точно равны отрицательным степеням числа 2. Алгоритм начинает строить кодовое дерево снизу вверх, затем скользит вниз по дереву, чтобы построить каждый индивидуальный код справа налево (от самого младшего бита к самому старшему). Начиная с работ Д.Хаффмана 1952 года, этот алгоритм являлся предметом многих исследований. (Последнее утверждение из § 3.8.1 показывает, что наилучший код переменной длины можно иногда получить без этого алгоритма.)
Алгоритм начинается составлением списка символов алфавита в порядке убывания их вероятностей. Затем от корня строится дерево, листьями которого служат эти символы. Это делается по шагам, причем на каждом шаге выбираются два символа с наименьшими вероятностями, добавляются наверх частичного дерева, удаляются из списка и заменяются вспомогательным символом, представляющим эти два символа. Вспомогательному символу приписывается вероятность, равная сумме вероятностей, выбранных на этом шаге символов. Когда список сокращается до одного вспомогательного символа, представляющего весь алфавит, дерево объявляется построенным. Завершается алгоритм спуском по дереву и построением кодов всех символов.
| <== предыдущая лекция | | | следующая лекция ==> |
| ПРОТОКОЛ | | | Про залучення захисника |