Товарознавча характеристика майонезу

Дата добавления: 2015-08-30; просмотров: 539

Одним из важных этапов синтеза оптимальной системы регулирования является разработка динамической модели ОУ, включающая:

1. определение структуры (порядка) конечно-разностного уравнения
2. определение численных значений параметров конечно-разностного уравнения заданной структуры.

Для этого используются соответственно методы структурной и параметрической идентификации. Параметрическая идентификация проверяется после выбора структуры объекта (порядка уравнения) на основе экспериментальных данных, значений входа и выхода, полученных по результатам снятия кривой разгона. Идентификация проводится для значений приращений, тоже и с величиной входного значения. Идентификация – это разработка дискретной динамической модели объекта регулирования на основе экспериментально-статистического подхода по экспериментальным данным входа и выхода.

Рассмотрим использование МНК для параметрической идентификации конечно-разностного уравнения второго порядка без запаздывания:

Критерий МНК имеет вид:

Таким образом, из критерия метода наименьших квадратов следует, что необходимо найти такие параметры конечно-разностного уравнения, которые обеспечили бы минимальные суммы квадратов разностей между экспериментальными значениями выхода и рассчитанными по модели. При определении расчетных значений выхода ОУ при идентификации могут быть использованы экспериментальные значения выхода и входа на предыдущих тактах квантования, т.е. . Тогда, подставляя правую часть записанного выражения в критерий метода наименьших квадратов, получим:

Полученная таким образом задача с точки зрения математики является задачей на поиск экстремума функционала Ф по параметрам a₁,a₂,b. Необходимое условие существование минимума является равенство нулю всех первых частных производных функционала Ф по неизвестным параметрам a₁,a₂,b, т.к. Ф является квадратичным функционалом, то необходимое условие является также и достаточным. Следовательно, возьмем частные производные и приравняем к нулю. После решим систему линейных уравнений относительно неизвестных a₁,a₂,b, в которой число уравнений равно числу неизвестных. Для взятия производных используется следующие правила дифференцирования:

1. дифференцирование функции нескольких переменных

2. взятие производной от суммы

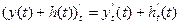
3. взятие производной от сложной функции

Получим:

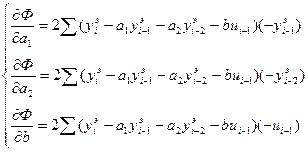
Приравнивая к нулю полученные производные, раскрывая скобки, в слагаемых, содержащих параметры , выносим их за знак суммы:

Выражения под знаком суммы, являются некоторыми коэффициентами, константами. Решая полученную систему линейных и однородных уравнений одним из известных аналитических методов (Гаусса, Крамара, матричный), находим искомые параметры . Осуществим проверку адекватности. В случае положительного результата (модель адекватна) получаем модель, которая принимается для последующего ее использования в задачах анализа и синтеза. При решении задач анализа динамических свойств объекта (задач моделирования по полученному конечно-разностному уравнению) расчет текущих значений выхода объекта осуществляется на основе значений выхода объекта, рассчитанных по этому же уравнению на предыдущих тактах квантования.

Обобщая полученные выкладки для конечно-разностного уравнения n-го порядка получим: 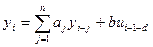. Критерий метода наименьших квадратов примет вид: . Тогда частные производные по искомым параметрам примут вид:

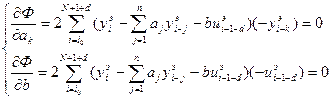
Перед использованием экспериментальных значений входа и выхода для идентификации необходимо сформировать массивы их экспериментальных значений с учетом приведенных начальных условий. Начальные условия будут иметь следующий вид:

где . Под подразумеваются ненулевые значения входа и выхода приращения.