Формування асортименту додаткових послуг.

Дата добавления: 2015-08-30; просмотров: 518

Цифровой регулятор в общем виде может быть представлен конечно-разностным уравнением m-го порядка.

Структурная схема регулятора:

,

где 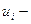выход регулятора (регулирующее воздействие),

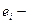ошибка регулирования сигнала рассогласования,

настроечные параметры цифрового регулятора,

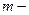порядок цифрового регулятора.

Ошибка регулирования определяется следующим выражением: ,

где 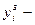задающее воздействие,

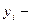текущее значение регулируемой величины.

Подставляя правую часть в уравнение регулятора получим: .

Получим конечно-разностное уравнение цифрового регулятора из дифференциального уравнения ПИД-регулятора: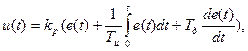

где коэффициент усиления,

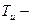время изодрома,

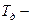время предварения.

Продифференцируем обе части уравнения, получим:

Заменим производные конечно-разностным уравнением, получим:

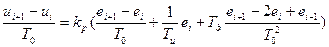. Выразим

: .

Понизим индекс на единицу:

Полученное уравнение называется конечно-разностным уравнением цифрового регулятора второго порядка, где настроечные параметры. Полученное уравнение позволяет выполнить следующее:

1. параметры цифрового регулятора можно вычислить по настройкам , что позволяет реализовать аналоговый регулятор с помощью цифровой вычислительной техники

2. из уравнения взаимосвязи настроек цифрового и аналогового регуляторов видно, что они равны по количеству, т.е. настройка цифрового равна настройке аналогового регулятора

3. из уравнения взаимосвязи видно, что размерность настроек цифрового регулятора совпадает с размерностью настроек аналогового регулятора

Для получения конечно-разностного уравнения ПИ регулятора необходимо постоянную дифференцирования приравнять к нулю. Дифференциальное уравнение ПИ-регулятора:

Цифровые настройки будут равны: , ,

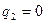
Следовательно цифровой ПИ-регулятор примет вид: 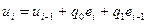. Построим график переходного процесса для регулятора первого порядка (цифровой ПИ-регулятор) при подаче на его вход единичного ступенчатого воздействия. Для этого укажем ограничения для , необходимые для реализации ПИ-закона в цифровом виде:

1. 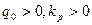или

2. или для ПИ-регулятора

3. при условии, что

Расчет переходного процесса по конечно-разностным уравнениям должен выполнятся на основе начальных условий, которые примут вид: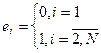

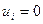
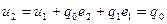
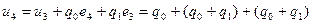
Построим переходной процесс для ПИД-закона в цифровом виде. Для этого запишем ограничения на настройки цифрового регулятора, обеспечивающие реализацию ПИД закона. При этом .

1.

2.

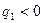
3.

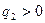
4.

5.

6.

7.

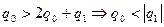
Для расчета переходного процесса цифрового ПИД-регулятора зададим начальные условия:

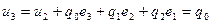
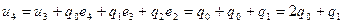
Цифровой регулятор, описывающийся конечно-разностным уравнением, охватывает больший класс законов регулирования, чем аналоговый. При выполнении ограничений на настройки цифрового регулятора они реализуют аналоговые законы. В противном случае – чисто цифровые законы регулирования.

Внимание! При выводе конечно-разностных уравнений цифровых регуляторов дифференцируют обе части уравнений аналогового регулятора только в том случае, когда есть интегрирующая составляющая.

Для регулятора, описываемого конечно-разностным уравнением m-го порядка, в общем случае . Начальные условия для расчета переходного процесса будут иметь вид: