Додаток Д.11 – Характеристики легкових автомобілів

Дата добавления: 2015-08-30; просмотров: 453

Запустить диалоговую систему Excel. Ввести данные для проведения регрессионного анализа. Окно с исходными данными представлено на рисунке 1.

Рисунок 1. Таблица с исходными данными.

Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов по данным в соответствии с вариантом.

Для построения линейного уравнения множественной регрессии воспользуемся инструментом анализа данных Регрессия. Порядок действий следующий:

а) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;

б) заполните диалоговое окно ввода данных и параметров ввода (рис. 2). При заполнении параметра входной интервал Х в диалоговом столбце следует указать все столбцы, содержащие значения факторных признаков.

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал Х – диапазон, содержащий данные факторов независимого признака;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист - можно задать произвольное имя нового листа.

Рисунок 2 – Диалоговое окно ввода параметров инструмента Регрессия

Результаты регрессионного анализа представлены на рисунке 3.

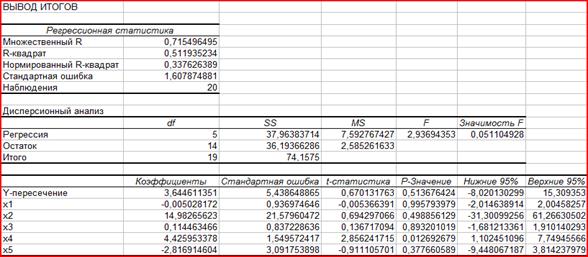
Рисунок 3 – Результат применения инструмента Регрессия

По результатам вычислений составим уравнение множественной регрессии:

Величина b₀ не интерпретируется.

Коэффициенты регрессии показывают среднее изменение результативного признака с изменением на 1 единицу своего измерения данного фактора при условии постоянства всех остальных.

Коэффициент чистой регрессии b₁ = -0,005 указывает, что с увеличением числа колесных тракторов на единицу на 100 га, урожайность снижается на 0,005 ц/га, при фиксированном значении остальных факторов. Для остальных коэффициентов делаются аналогичные выводы. Сравнивать коэффициенты чистой регрессии не следует, так как они зависят от единиц измерения каждого признака и потому не сопоставимы между собой.

Следует отметить, что отрицательные знаки коэффициентов регрессии в нашем примере противоречат экономической теории связи между признаками.